Примеры и задачи.

Пример 1. Дан ряд распределения случайной величины :

> matrix([[-2, -1, 0, 1, 2], [0.1, 0.2, 0.2, 0.4, 0.1]]);

Построить функцию распределения случайной величины , вычислить вероятность попадания случайной величины в интервал [-1; 2).

Решение. Функция распределения случайной величины:

> F:=x->piecewise(x<-2,0,x>=-2 and x<-1,0.1,x>=-1 and x<0,0.3,x>=0 and x<1,0.5,x>=1 and x<2,0.9,x>=2,1):'F(x)'=F(x);#Функция распределения

Построим график функции распределения:

> plot(F(x),axes=boxed);#График F(x)

Чтобы вычислить вероятность того, что случайная величина примет значение из интервала [-1; 2), воспользуемся формулой

и получим искомую вероятность:

> "P(-1<=x<2)"=F(2)-F(-1);# Вероятность попадания в интервал [-1;2)

Задача 1. Бросают пять монет. Требуется: а) задать случайную величину , равную числу выпавших "решеток"; б) построить ряд распределения и функцию распределения случайной величины , если вероятность выпадения "герба" равняется 0.5; в) построить график функции распределения; г) найти вероятность того, что выпадет не более 2-х "решеток".

Пример 2. Случайная величина задана функцией распределения:

> restart:F:=x->piecewise(x<2,0,x>=2 and x<3,(x-2)^2,x>3,1):'F(x)'=F(x);

Найти плотность вероятности , построить графики F и f, вычислить вероятность попадания случайной величины в интервал [1; 2.5).

Решение. Найдем плотность вероятности случайной величины :

> f:=diff(F(x), x);

Заметим, что в точке x=3 производная функции F(x) не существует.

Построим графики функций F(x) и f(x).

> plot([F(x),f],x=-10..10,color=[black,black],linestyle=[solid, spacedot],axes=boxed);#Графики F(x) и f(x)

График f(x) построен пунктиром.

Пользуясь свойством функции распределения, вычислим вероятность попадания случайной величины в интервал [1; 2.5),

> "P(1<=x<2.5)"= F(2.5)-F(1);# Вероятность попадания в интервал [-1;2)

Задача 2. Дана функция распределения случайной величины (нормальное распределение с параметрами (0,1)).

> F(x):=1/sqrt(2*Pi)*Int(exp(-t^2/2),t=-infinity..x);

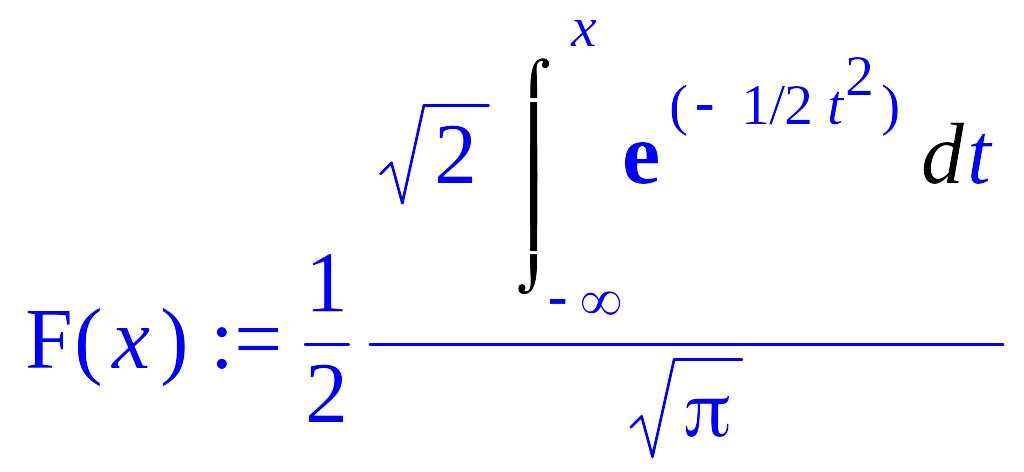
Найдите плотность вероятности f(x), постройте графики функций f(x) и F(x), вычислите вероятность попадания случайной величины в интервал [-2; 5).

Задача 3. Случайная величина имеет плотность распределения

> f(x):=piecewise(x<=0,0,x>0 and x<=Pi,0.5*sin(x),x>Pi,0);

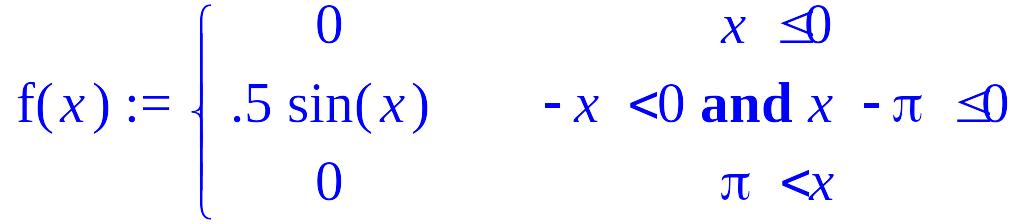
а) Построить функцию распределения F(x); b) найти вероятность того, что в результате испытания величина примет значение, заключенное в интервале [0, /4).

Пример 3. Пусть и .

> restart:

> assume(lambda>0):assume(x>=0):#Ограничения

Плотность вероятности случайной величины равна

> f:=A*x^2*exp(-lambda*x);#Плотность вероятности

Построить функцию распределения F случайной величины , вычислить значение A, найти вероятность попадания случайной величины в интервал [0, ).

Решение. Найдем функцию распределения, для чего подставим в функцию f вместо x переменную t и проинтегрируем f по t от 0 до x:

> f:=subs(x=t,f):F:=int(f,t=0..x);#Функция распределения

Найдем коэффициент А, используя тот факт, что интеграл от функции f от 0 до бесконечности равен 1

> 'A'=solve(int(f,t=0..infinity)-1,A);# Определение А

Для вычисления вероятности попадания случайной величины в интервал [0, ) подставим в функцию F найденное значение A

> subs(A=1/2*lambda^3,F):F:=unapply(%,x);#Подстановка А

Вычислим искомую вероятность:

> Digits:=2:p:=evalf(F(1/lambda)-F(0));# Вероятность попадания в интервал

Задача 4. Плотность вероятности случайной величины равна (Закон гиперболического секанса)

> f:=A/(exp(x)+exp(-x));

Найти: а) коэффициент А; б) вероятность того, что в двух независимых наблюдениях примет значения, меньшие 1.

Задание на практическое занятие. Внимательно ознакомьтесь с приведенными выше примерами. Решите задачи. Сделайте выводы и оформите отчет по работе.

В отчете необходимо приводить условие решаемой задачи, излагаться ход её решения (обозначение событий, ссылки на определения и теоремы, в необходимых случаях – поясняющие рисунки, формулы, вычисления), результат и его оценка. Бумажный вариант отчета должен быть проверен и подписан студентом.