Задачи для самостоятельного решения

Задача 1. Постройте пространство элементарных событий для опыта с бросанием монеты один раз. Определите вероятность следующих событий: «выпадение орла», «выпадение решки», «хотя бы выпадение орла».

Задача 2. Постройте пространство элементарных событий для опыта с бросанием двух монет один раз. Определите вероятность того, что на обеих монетах выпадет «орёл».

Задача 3. Постройте пространство элементарных событий для опыта с бросанием монеты два раза. Определите вероятность того, что оба раза выпадет «орёл».

Задача 4. Постройте пространство элементарных событий для опыта с бросанием двух игральных костей один раз. Определите вероятность того, что на одной из костей выпадет цифра «три».

Задача 5. Точка бросается на поверхность круга радиуса . Какова вероятность попадания точки в квадрат, вписанный в окружность? Каково противоположное событие и какова его вероятность? Попадание точки в круг считать достоверным событием.

Задача 6. Производятся опыты с подбрасыванием монеты. В первом опыте монета была подброшена 10 раз, а «орел» выпал 8 раз. Данные по трем последующим опытам следующие: число подбрасываний – 40, число «орлов» - 18, число подбрасываний – 70, число «орлов» - 36, число подбрасываний – 100, число «орлов» - 50. Определите частоты появления «орла» в каждом опыте и сделайте выводы о вероятности выпадения орла при подбрасывании монеты.

Задание на практическую работу

Решите самостоятельно указанные преподавателем задачи. Сделайте выводы и оформите отчет по работе. В отчете необходимо приводить условие решаемой задачи, излагаться ход её решения (обозначение событий, ссылки на определения и теоремы, в необходимых случаях – поясняющие рисунки, формулы, вычисления), результат и его оценка. Бумажный вариант отчета должен быть проверен и подписан студентом.

Вопросы для самоконтроля

1. Что такое событие? Приведите примеры событий.

2. Как классифицируются события?

3. Что такое вероятность?

4. Дайте геометрическое определение вероятности.

5. Дайте статистическое определение вероятности.

6. Дайте классическое определение вероятности.

7. Что такое "элементарное событие"?

8. Что такое "пространство элементарных событий"?

9. Что такое "полная группа событий"? Приведите примеры.

10. Что такое "благоприятствующее событие"?

11. Что такое "сумма событий"?

12. Что такое "произведение событий"?

Тема №2

Элементы комбинаторики

Теоретическое введение примеры и задачи

Многие задачи теории вероятностей требуют подсчета количества комбинаций элементов, факторов или обстоятельств. Такими подсчетами занимается специальный раздел математики, названный комбинаторикой. Основными понятиями комбинаторики являются перестановки, сочетания и размещения.

Одним из элементов комбинаторных формул является факториал - произведение натуральных чисел. Факториал обозначается восклицательным знаком «!». Например, пять-факториал:

,

n-факториал:

,

частное от деления двух факториалов:

.

По определению принято

и

1 Перестановки

Перестановками называются такие комбинации из n элементов, которые отличаются только порядком следования элементов.

Например, комбинации из четырех цифр

1234, 2341, 3421, 1243, 4231, … .

являются перестановками без повторений. Комбинации

1231, 2311, 3121, 1132, 2113, …

являются перестановками из трех цифр с повторениями, в которых цифра 1 повторяется два раза.

Число перестановок из n элементов (без повторения элементов) рассчитывается по формуле

Если же элементы могут повторяться: первый элемент раз, второй элемент раз, … , - тый элемент раз, то общее количество элементов равно

,

а число перестановок рассчитывается по формуле

Maple имеет специальный модуль (библиотеку) combinat в которой собраны команды, реализующие комбинаторные вычисления. Так, генерирование всех перестановок осуществляется командой permute.

Генерируем всевозможные перестановки из четырёх различных элементов - цифр:

> P:=combinat[permute](4);

Найдем количество всевозможных перестановок из 4 элементов

> combinat[numbperm](4);

К примеру, в случайном порядке выписывают элементы a, b, c, d. Требуется найти вероятность того, что символы a и b окажутся рядом, сначала a, затем b. Получим всевозможные перестановки из a, b, c, d:

> P:=combinat[permute]([a,b,c,d]);

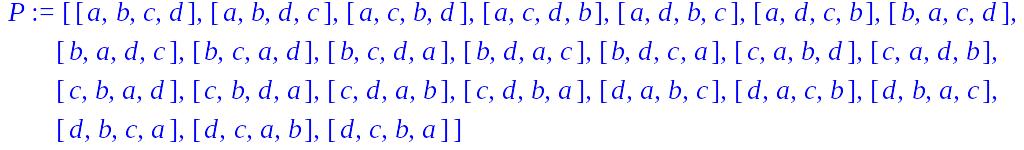
Всего перестановок из четырех элементов 24. Сгенерируем перестановки из элементов ab,c,d

> Pab:=combinat[permute]([ab,c,d]);

Всего элементов 6. Тогда искомая вероятность равна .

Задача 1. Сколько целых девятизначных чисел можно составить из цифр 1,2,3,4,5,6,7,8,9, не повторяя их дважды? Приведите пример такого числа.

Задача 2. Сколько семизначных чисел можно составить из цифр 4,5, и 6, в которых цифра 4 повторяется 2 раза, цифра 5 – 3 раза, цифра 6 – 2 раза. Приведите примеры таких чисел.

Задача 3. На полке в случайном порядке расставлено 7 книг, среди которых находится двухтомник Д. Лондона. Предполагая, что различные расположения книг равновозможны, найти вероятность того, что оба тома двухтомника расположены рядом.

2 Сочетания

Сочетаниями (или биномиальными коэффициентами) называются такие неупорядоченные комбинации из элементов по элементам, которые отличаются только составом элементов. Например, из пяти элементов сочетаниями по три элемента будут комбинации

.

Сочетаниями с повторениями из тех же элементов будут комбинации

.

Числа сочетаний из элементов по вычисляются по следующим формулам

для сочетаний без повторений,

для сочетаний с повторениями.

Ниже приводятся примеры использования средств Maple для работы с сочетаниями.

2.1 Непосредственное вычисление факториалов

Создадим функции для вычислений числа сочетаний и числа сочетаний с повторениями

> C:=unapply(n!/m!/(n-m)!,n,m);

> Crepet:=unapply((n+m-1)!/m!/(n-1)!,n,m);

Вычислим число сочетаний из 15 по 3 без повторений

> 'C(15,3)'=C(15,3);

Вычислим число сочетаний из 15 по 3 с повторениями

> 'Crepet(15,3)'=Crepet(15,3);

Вычислим число сочетаний из 15 по 1 без повторений

> 'C(15,1)'=C(15,1);

Вычислим число сочетаний из 15 по 1 с повторениями

> 'Crepet(15,1)'=Crepet(15,1);

2.2 Использование средств модуля combinat

Вычисление числа сочетаний производится с помощью команды binomial.

Приведем примеры её использования. Числа сочетаний из 5 по 2, из 5 по 3 и из 6 по 4 без повторений равны

> binomial(5, 2);

> binomial(5, 3);

> binomial(6, 4);

Число сочетаний из 6 по 4 с повторениями вычисляется посредством замены на

> binomial(9, 4);

В общем случае, функция числа сочетаний из по с повторениями реализуется командой

> Crepet:=unapply(convert(binomial(n+m-1,m),factorial),n,m);

или её более простым вариантом

> Crepet:=unapply(binomial(n+m-1, m),n,m);

2.3 Задачи

Задача 4. Имеются различные цветы 12 видов. Сколько букетов можно из них составить если в состав каждого букета включать по 5 цветов различных видов?

Задача 5. Сколько партий необходимо сыграть в шахматном турнире 15 участникам, если каждая пара шахматистов играет дважды, изменяя цвета фигур во второй партии.

Задача 6. Имеется квадратная матрица размером элементов.

1. Каково суммарное количество элементов, лежащих на главной диагонали и выше её?

2. Какой будет вероятность выбора из них элемента первой строки, если считать, что выбор одного из элементов, лежащих на главной диагонали и выше её, является достоверным событием.

3 Размещения

Если комбинации из элементов по отличаются либо составом, либо порядком элементов, но имеются и те, и другие отличия, то такие комбинации называются размещениями из элементов по .

Например, комбинации из девяти десятичных цифр (без нуля) по три 123,456, 387, 639, 132, 378 …, являются размещениями. Действительно, первая комбинация (123) отличается от второй (456), третьей (378), четвертой (639) и шестой (378) составом элементов, а от пятой (132) – порядком следования элементов. В комбинациях имеются и те, и другие отличия.

Если же элементы могут повторяться, то говорят о размещениях с повторениями. Продолжая предыдущий пример, запишем размещения с повторениями: 123,455, 387, 639, 132, 333 … .

Числа размещений из элементов по вычисляются по следующим формулам

- для размещений без повторений,

- для размещений с повторениями.

Ниже приводятся примеры использования средств Maple для работы с размещениями.

3.1 Типовые средства

Типовые средства используются для «ручного» программирования формул. Так формулы для чисел размещений без повторений и с повторениями реализуются следующим Maple – фрагментом.

> restart:

> A:=unapply(n!/(n-m)!,n,m);

> Arepet:=unapply(n^m,n,m);

Теперь вычисление числа размещений сводится к обращению к соответствующей функции. Вычислим, например, числа размещений из 9 по 3 без повторений и с повторениями

> 'A(9,3)'=A(9,3);

> 'Arepet(9,3)'=Arepet(9,3);

3.2 Средства модуля combinat

Загрузим программный модуль с библиотекой комбинаторики.

> restart: with(combinat);

Размещения генерируются командой permute, а их количество подсчитывается командой numbperm.

Генерируем все размещения (без повторений) из 5 по 2

> permute(5, 2);

Подсчитаем их число

> numbperm(5, 2);

3.3 Задачи

Задача 7. В некоторой местности имеется 15 женихов и 15 невест. Сколько вариантов брачных пар можно составить из них. Какова вероятность каждого варианта бракосочетания, если считать факт бракосочетания по одному из вариантов достоверным?

Задача 8. В лифт на первом этаже девятиэтажного здания вошли четыре пассажира. Каждый из пассажиров, независимо от других, может выйти из лифта на любом этаже, со 2-го по 9-й.

1. Сколько различных вариантов выхода пассажиров из лифта существует?

2. Какова вероятность того, что все пассажиры выйдут на 6-м этаже?

3. Какова вероятность того, что все пассажиры выйдут на одном этаже?

Задание на практическое занятие

Тщательно разберитесь с приведенными выше примерами решения типовых задач. Решите указанные преподавателем задачи. Сделайте выводы и оформите отчет по работе. В отчете необходимо приводить условие решаемой задачи, излагаться ход её решения (обозначение событий, ссылки на определения и теоремы, в необходимых случаях – поясняющие рисунки, формулы, вычисления), результат и его оценка. Бумажный вариант отчета должен быть проверен и подписан студентом.

Вопросы для самоконтроля

1. Что такое "комбинаторика"?

2. Что такое "факториал"? Как он вычисляется?

3. Что такое "перестановки"?

4. Приведите примеры и формулы для вычисления числа перестановок с повторениями и без повторений.

5. Что такое "сочетания"?

6. Приведите примеры и формулы для вычисления числа сочетаний с повторениями и без повторений.

7. Что такое "размещения"?

8. Приведите примеры и формулы для вычисления числа размещений с повторениями и без повторений.

9. Каковы инструментальные средства среды Maple для работы с перестановками, сочетаниями и размещениями.

Тема №3

Теоремы сложения и умножения вероятностей