Многослойный персептрон и алгоритм обратного распространения ошибки

Следующий период истории персептронов начался с появления книги М. Минского и С. Пайперта «Персептроны». В этой книге математически строго было доказано, что использовавшиеся в то время однослойные персептроны в принципе не способны решать многие простые задачи.

Эффективный алгоритм обучения многослойных персептронов открывший путь для их широкого практического применения стал известен только в 1986г., благодаря работе Румельхарда, Хилтона и Вильямса. Данный фундаментальный алгоритм называется алгоритмом обратного распространения ошибки.

Рассмотрим алгоритм обратного распространения ошибки для многослойного персептрона (рис.5), имеющего входной слой k=0, несколько скрытых слоев k=1, 2, …, K1 и выходной слой k=K.

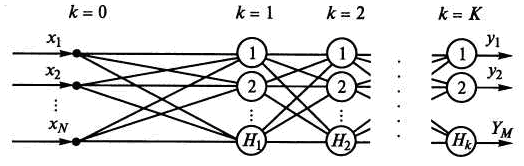
Рис.5. Многослойный персептрон

Нейроны входного слоя математических преобразований не выполняют, а лишь передают входные сигналы нейронам первого слоя. Будем полагать, что каждый кй слой содержит Н_к нейронов. Таким образом, персептрон имеет N = Н_о входов и М = Н_К выхо­дов. В алгоритме будем использовать следующие обозначения: i  порядковый номер нейрона k-го слоя; j  порядковый номер ней­рона (к  1)-го слоя; l  порядковый номер нейрона (к + 1)-го слоя.

Шаг 1. Инициализация синаптических весов и смещений.

В циклах по k= 1, 2, ..., К; i= 1, 2, ..., Н_к, j = 1, 2, ..., Н_к-1 синаптическим весам и смещениям w_ij^(k) датчиком случайных чи­сел присваиваются малые величины, например, из интервала от -1 до 1.

Шаг 2. Представление из обучающей выборки очередного входного вектора Х_q = (х₁, х₂, ..., x_N)_q и соответствующего ему желаемого выходного вектора D_q = (d₁, d₂, ..., d_M)_q, где q – номер примера в обучающей выборке.

Шаг 3. Прямой проход.

В циклах по k = 1, 2, ..., К; i = 1, 2, ..., Н_к вычисляются выходные сигналы i-го нейрона в к-м слое

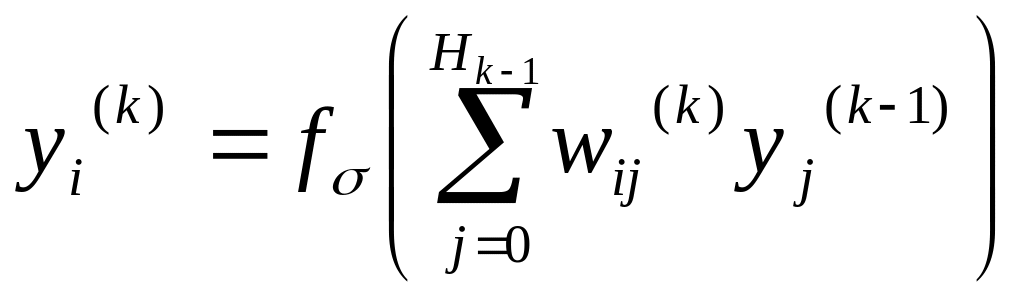(4)

где , , , и выходные сигналы персептрона .

Шаг 4. Обратный проход.

В циклах по k = К, K1, …, 1; i = 1, 2, ..., Н_к, j = 1, 2, ..., Н_к-1 вычисляются синаптические веса на новой эпохе

(5)

где

(6)

причем для выходного слоя k=K

а для всех других случаев

(7)

Шаг 5. Повторение шагов 2 – 4 необходимое число раз.

Входные векторы обучающих примеров X_q и D_q на втором шаге алгоритма обычно представляются последовательно от первого до последнего, т.е. q = 1, 2, ..., Q, где Q – общее число примеров. Например, в случае распознавания букв русского алфавита Q = 33. После того как для каждого обучающего примера будут скорректированы весовые коэффициенты персептрона, т. е. шаги 2–4 будут повторены 33 раза, на пятом шаге алгоритма вычисляется среднеквадратичная ошибка, усредненная по всем обучающим примерам:

(8)

Итерационный процесс заканчивается после того, как среднеквадратичная ошибка достигнет заданной величины, либо при достижении предельного числа эпох обучения. В результате персептрон обучится выполнять нужное отображение любого входного вектора Х_q на выходной вектор Y_q, отличающийся от желаемого вектора D_q на некоторую малую величину.

Модели нейронных сетей

1. Математический нейрон.

2. Однослойный персептрон.

3. Многослойный персептрон. В многослойных сетях устанавливаются связи только между нейронами соседних слоев, как показано на рис. 6.

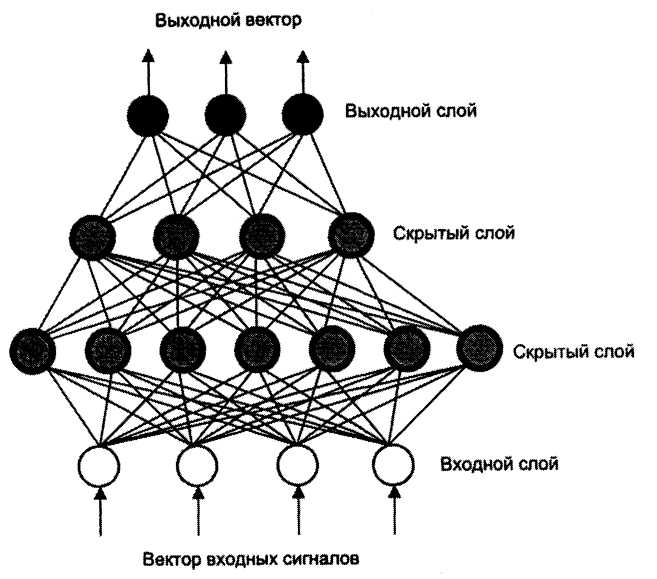
Рис. 6. Схема многослойного персептрона

Каждый элемент может быть соединен модифицируемой связью с любым нейроном соседних слоев, но между элементами одного слоя связей нет. Каждый нейрон может посылать выходной сигнал только в вышележащий слой и принимать входные сигналы только с нижерасположенного слоя. Входные сигналы подаются на нижний слой, а выходной вектор сигналов определяется путем последовательного вычисления уровней активности элементов каждого слоя (снизу вверх) с использованием уже известных значений активности элементов предшествующих слоев. При распознавании образов входной вектор соответствует набору признаков, а выходной – распознаваемым образам. Скрытый слой (один или несколько) предназначен для отражения специфики знаний. В таких сетях обычно используются передаточные сигмоидальные функции.

4. Рекуррентные сети. Они содержат обратные связи, благодаря которым становится возможным получение отличающихся значений выходов при одних и тех же входных данных. Наличие рекуррентных нейронов позволяет ИНС накапливать знания в процессе обучения.

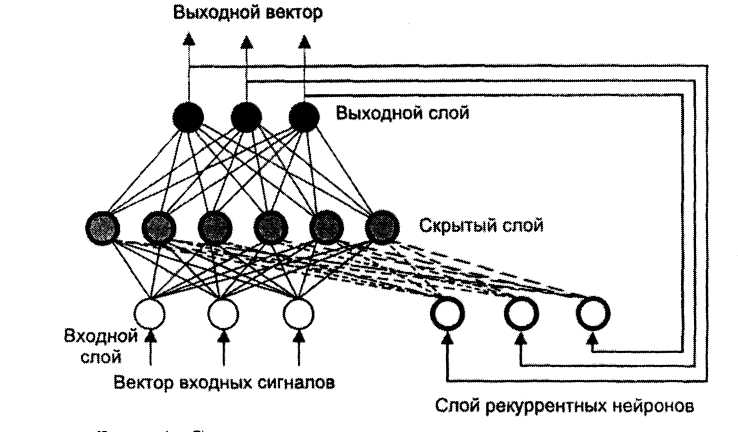
Рис. 7. Схема рекуррентной нейронной сети

Для всякой рекуррентной сети может быть построена идентичная сеть без обратных связей с прямым распространением сигнала, поэтому для обучения рекуррентных сетей может быть применен метод обратного распространения ошибки.

5. Модель Хопфилда. Работы американского биофизика Дж. Хопфилда положили начало современному математическому моделированию нейронных вычислений. Ему удалось привлечь к анализу нейросетевых моделей мощный математический аппарат статистической физики. В результате была сформулирована математическая модель ассоциативной памяти на нейронной сети с использованием правила Хебба для модификации весовых коэффициентов.

Сеть Хопфилда в классическом варианте исполнения приведена на рис.8.

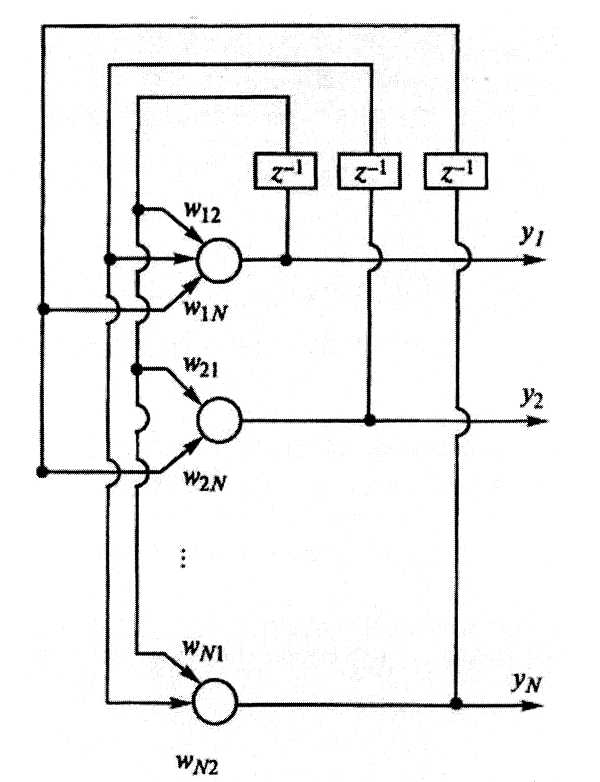
Рис.8. Сеть Хопфилда

Считается, что она не имеет входных элементов, а входной вектор задает первоначальную активность нейронов, которая затем изменяется в ходе итерационного процесса, обусловленного наличием обратных связей. Согласно рис. 5 в схеме отсутствуют связи нейронов с их собственными выходами.

Сеть работает следующим образом. Сначала входной вектор задает начальную активность y_i(t) каждого нейрона. Затем выбранный случайным образом нейрон получает взвешенные сигналы от всех остальных нейронов и обновляет свое состояние

Выбирается следующий нейрон, и процесс повторяется до тех пор, пока нейроны, выбранные для обновления, не перестанут изменять свое состояние. Наступает стационарный режим.

Сеть Хопфилда ведет себя подобно памяти, хранящей некоторый заданный заранее набор образов, которая пытается вспомнить один из них, если ей предъявляется какой-либо из этих образов, искаженный помехами. Образы предварительно кодируются в виде векторов с бинарными компонентами. Каждый из векторов перемножается сам на себя, образуя квадратную матрицу. Затем матрицы складываются, образуя новую квадратную матрицу, главная диагональ которой обнуляется. Это и есть матрица синаптических весов w_ij хранящая информацию о всех заданных образах.

Сети Хопфилда получили применение на практике в основном как реализации подсистем более сложных систем. Они имеют определенные недостатки, ограничивающие возможности их применения:

• предположение о симметрии связей между элементами, без которой нельзя ввести понятие энергии;

• нейронная сеть – это устройство для запоминания и обработки информации, а не устройство минимизации энергии. Экономия энергии играет в этих процессах вспомогательную роль;

• сети Хопфилда поддерживают множество лишних, неэффективных, иногда дублирующих друг друга связей. В реальных нервных системах такие связи не поддерживаются, так как их реализация требует определенных затрат. В биологических нервных системах происходит освобождение от лишних связей за счет их структуризации. При этом вместо организации связей «всех ко всем» используется многослойная иерархическая система связей.

6. Самоорганизующиеся сети Т. Кохонена. Идея сетей с самоорганизацией на основе конкуренции между нейронами базируется на применении специальных алгоритмов самообучения ИНС. Сети Кохонена обычно содержат один выходной слой обрабатывающих элементов с пороговой передаточной функцией. Число нейронов в выходном слое соответствует количеству распознаваемых классов. Настройка параметров межнейронных соединений проводится автоматически на основе меры близости вектора весовых коэффициентов настраиваемых связей к вектору входных сигналов в эвклидовом пространстве. В конкурентной борьбе побеждает нейрон, имеющий значения весов, наиболее близкие к нормализованному вектору входных сигналов. Кроме того, в самоорганизующихся сетях возможна классификация входных образцов (паттернов). На практике идея Кохонена обычно используется в комбинации с другими нейросетевыми методами.