Елабужский филиал федерального государственного бюджетного образовательного учреждения высшего профессионального образования

«Казанский национальный исследовательский технический университет им. А.Н. Туполева – КАИ»

Лабораторная работа №6

по дисциплине

“Представление знаний”

Нейронные сети

Елабуга 2013

Лабораторная работа №6

Цель работы: изучение искусственных нейронных сетей как способа представления знаний о предметной области и моделирование работы в пакете Neural Networks Toolbox системы Matlab.

Теоретические сведения Мозг и компьютер

Нейронные сети и нейрокомпьютер – это одно из направлений компьютерной индустрии, в основе которого лежит идея создания искусственных интеллектуальных устройств по образу и подобию человеческого мозга. Прежде чем рассматривать такие устройства, приведем основные сведения о принципах организации и функционирования человеческого мозга.

Мозг человека состоит из белого и серого вещества: белое – это тела нейронов, а серое – соединяющие их нервные волокна. Каждый нейрон состоит из трех частей: тела клетки, дендритов и аксона.

Нейрон получает информацию через свои дендриты, а передает ее дальше через аксон, разветвляющийся на конце на тысячи синапсов – нервных нитей, соединяющих нейроны между собой (рис.1).

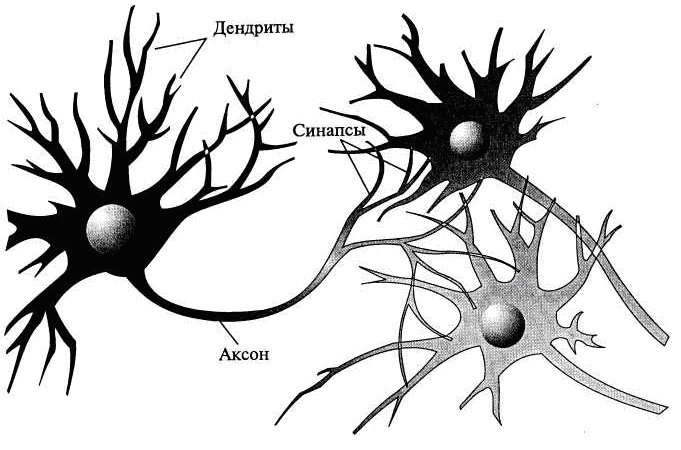
Рис.1. Нейроны человеческого мозга

Простейший нейрон может иметь до 10 000 дендритов, принимающих сигналы от других клеток. В человеческом мозге содержится приблизительно 10¹¹ нейронов. Каждый нейрон связан с 10³... 10⁴ другими нейронами. Таким образом, биологическая нейронная сеть, составляющая мозг человека, содержит 10¹⁴... 10¹⁵ взаимосвязей.

Каждый нейрон может существовать в двух состояниях – возбужденном и невозбужденном. В возбужденное состояние нейрон переходит под воздействием электрических сигналов, поступающих к нему от других нейронов, когда эти воздействия становятся достаточно большими. В возбужденном состоянии нейрон сам посылает электрический сигнал другим соединенным с ним нейронам.

Математический нейрон Мак-Каллока-Питтса

Исторически первой работой, заложившей теоретический фундамент для создания интеллектуальных устройств, не только функционально, но и структурно моделирующих человеческий мозг, принято считать опубликованную в 1943г. статью Уоррена Мак-Каллока и Вальтера Питтса. Ее авторы выдвинули гипотезу математического нейрона – устройства, моделирующего нейрон мозга человека. Математический нейрон тоже имеет несколько входов и один выход. Через входы, число которых обозначим J, математический нейрон принимает входные сигналы x_j, которые суммирует, умножая каждый входной сигнал на некоторый весовой коэффициент w_j.

(1)

Выходной сигнал нейрона у может принимать одно из двух значений – нуль или единицу, которые формируются следующим образом:

(2)

(3)

где  – порог чувствительности нейрона.

Таким образом, математический нейрон, как и его биологический прототип, существует в двух состояниях. Если взвешенная сумма входных сигналов S не достигает некоторой пороговой величины , то математический нейрон не возбужден и его выходной сигнал равен нулю. Если же входные сигналы достаточно интенсивны и их сумма достигает порога чувствительности, то нейрон переходит в возбужденное состояние и на его выходе образуется сигнал у=1. Весовые коэффициенты w_j имитируют электропроводность нервных волокон – силу синаптических связей между нейронами. Чем они выше, тем больше вероятность перехода нейрона в возбужденное состояние. Логическая функция (2) – (3), называемая активационной функцией нейрона, графически изображена на рис. 2.

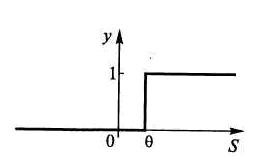
Рис.2. Пороговая активационная функция нейрона

Таким образом, математический нейрон представляет собой пороговый элемент с несколькими входами и одним выходом. Одни из входов математического нейрона оказывают возбуждающее действие, другие – тормозящее. Каждый математический нейрон имеет свое определенное значение порога.

Математический нейрон обычно изображают кружочком, возбуждающий вход – стрелкой, а тормозящий – маленьким кружочком. Рядом может записываться число, показывающее значение порога . Как показано на рис. 3, математические нейроны могут реализовывать различные логические функции. Так, математический нейрон, имеющий два входа с единичными силами синаптических связей w₁ = w₂ = 1, согласно формулам (1) – (3) реализует функцию логического умножения «И» при  = 2 и функцию логического сложения «ИЛИ» при =1. Нейрон с одним входом, у которого w = -1, реализует логическую функцию «НЕТ» при  = 0.

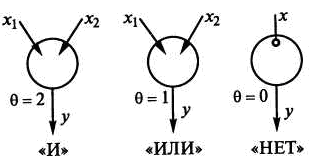
Рис.3. Математические нейроны, реализующие логические функции