3.2.3. Рынок финансов

Сбережения делают одни агенты, а инвестируют другие. Чтобы действительно сделать инвестиции, надо на рынке продукта купить фондообразующий продукт, а для этого нужны деньги. То же верно и в отношении потребителя. Кейнс предполагает, что деньги выпускает государственный банк и считает предложение денег заданным управляющим параметром. Относительно спроса на деньги Кейнс делает ещё одно существенное предположение:

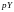8) спрос на деньги представляет собой сумму операционного и спекулятивного спроса. Операционный спрос на деньги покрывает потребности совершать сделки на рынке. Если цена продукта , то платежи в единицу времени (поток) можно оценить как . А если характерное время обращения денег (запаздывание платежей по отношению к поставкам) оценивается величиной τ, то количество денег, которое надо иметь на руках, чтобы производить покупки товары _, можно оценить как 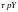. Это и есть операционный спрос.

Деньги как платежные средства имеют разную ликвидность — способность обмениваться на продукт. Самая высокая ликвидность у банкнот, у облигаций ликвидность меньше, но они приносят доход в виде процента. Облигациями неудобно оплачивать текущие расходы, но инвестиции ими оплачивают. Владельцы денег вольны сами выбирать ликвидность денег: могут держать дома банкноты, а могут на них купить в банке облигации, пустив банкноты в оборот. Если норма процента высока, то большую часть денег их владельцы предпочитают хранить в банке, рассчитывая на хороший доход и жертвуя более высокой степенью ликвидности банкнот в сравнении с банковскими обязательствами. При низкой процентной ставке спекулятивный спрос увеличивается: владельцы желают иметь на руках все больше банкнот, аккумулируя в них свои накоп­ления, выжидая, пока норма процента повысится. 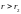Это спекулятивный спрос на деньги , он зависит от нормы процента, так что при и резко возраста при 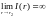_. Последнее условие называется ловушкой ликвидности и означает, что если норма процента меньше 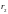, владельцы денег теряют интерес к ценным бумагам.

Итак, общий спрос на деньги равен 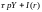, и условие равновесия рынка денег (баланс денег в экономической системе)

(3.6)

дает еще одну связь спроса на продукт с его ценой и нормой процента при заданной величине предложения .

Система уравнений (3.1), (3.2), (3.4), (3.6) описывает состояние равновесия рыночной экономики, определяя математическую модель рыночного равновесия.

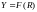
(3.7)

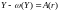
В модели (3.7) задаются параметры системы (ставка заработной платы), (предложение денег) и технический параметр . Функции 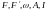— известные функции своих аргументов с описанными выше свойствами. По этим входным данным из модели определяются четыре неизвестных величины: (выпуск продукта), (занятость), (цена продукта) и (норма прибыли).

_Исключая из (3.7) величины уравнения (3.7) легко свести к одному уравнению относительно

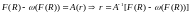
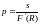
Подставляя полученные выражения для p,r и Y, получим

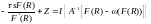
_(3.8)

_.

_{Определив из (3.8) значение , из (3.7) нетрудно определить все остальные искомые величины.}

_{Докажем су}ществование решения уравнения (3.8) относительно неизвестной _{на основе анализа графиков функций, входящих в его левую и правую части.}

Рис. 4 Рис.5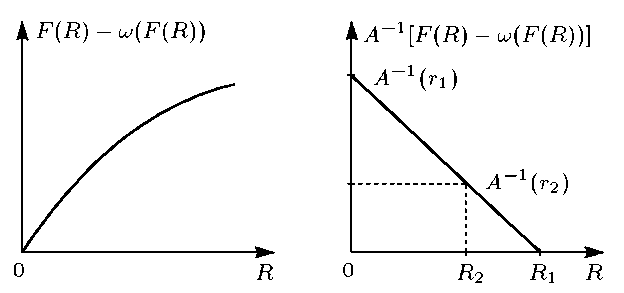

Функция — монотонно растущая функция , равная нулю при 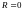(рис. 4). Ее монотонность следует из условия

, .

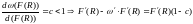Данная функция является аргументом для монотонной функции 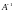, и из свойств функции (рис. 3) легко установить качественный вид зависимости от (рис.5), причем 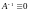при 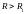( некоторое значение величины , 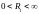). В свою очередь служит аргументом монотонной функции , свойства которой таковы (рис.3), что как функция она имеет вид, изображенный на рис.6 (для значений функция не определена).

Рис.6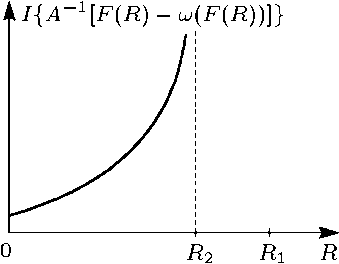

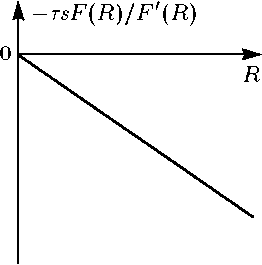
_Рис.7

_{Рассмотрим} теперь левую часть уравнения (3.8). Функция 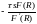равна нулю при 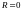(считается, что 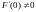); (см. рис.2). Вычислим её первую производную по _:

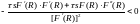
Её отрицательность следует из свойств функций , . Таким образом, монотонно убывает (рис. 7).

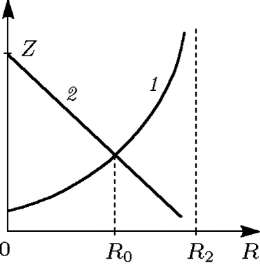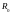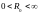С овмещая графики левой (кривая 2) и правой (кривая 1) частей уравнения (3.8) на одном рис. 8, убеждаемся в том, что при достаточно большом значении управляющего параметра кривые пересекаются в некоторой точке , . Точка пересечения единственна в силу монотонности графиков. Следовательно, модель (3.7) действительно имеет единственное решение, описывающее равновесное состояние экономики.

_{Рис. 8}

Модель равновесия использовалась, например, для разработки плана стабилизации французской экономики в 1963 г. И хотя некоторая стабилизация была достигнута, Л. Столерю¹ очень осторожно высказывается относительно того, насколько велика была роль модели, да и самого плана в стабилизации экономического развития.