Геометрические приложения определенного интеграла

Определение определённого интеграла как предела интегральных сумм позволяет получить различные формулы для нахождения длин, площадей и объёмов геометрических объектов.

Найдем площадь криволинейной трапеции в декартовой системе координат, ограниченной линиями:

у = f₁ (x), y = f₂ (x), х = a, x = b.

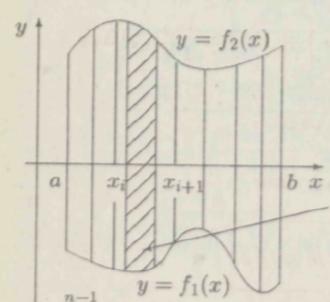
Пример 3. Вычислить площадь, ограниченную линиями:

Решение. Представим на графике указанную площадь. Для этого вычертим параболу и прямую , а затем выделим фигуру, заключенную между этими геометрическими объектами. Вычисление площади этой фигуры с помощью определенного интеграла потребует знания пределов интегрирования. Это нижняя и верхняя границы проекции фигуры на ось абсцисс. Для нахождения таких границ приравняем правые части заданных уравнений: x²-x+3=7-x. Отсюда x²-4=0. Значит, x₁=-2, x₂=2.

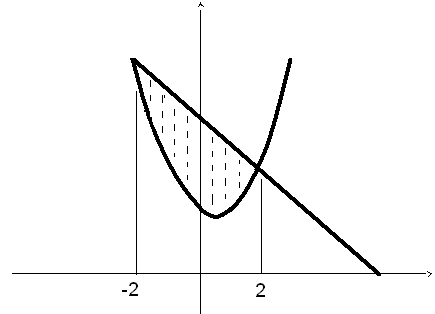
Площадь выделенного участка вычислим с помощью определенного интеграла:

Найдем площадь криволинейного сектора в полярной системе координат, ограниченного линиями: кривой ρ = ρ (φ) и лучами φ = α, φ = β.

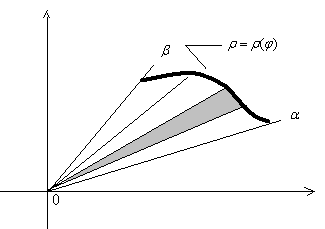
Площадь выделенного узкого треугольника можно вычислить по формуле:

или, в силу первого замечательного предела, при малом

Переходя к пределу при и , получаем

Итак, площадь криволинейного сектора можно вычислить по формуле:

Пример 4. Найти площадь трилистника, если длина лепестка равна а.

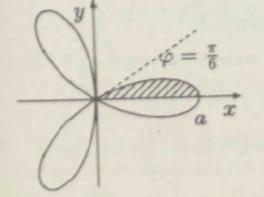
Решение.

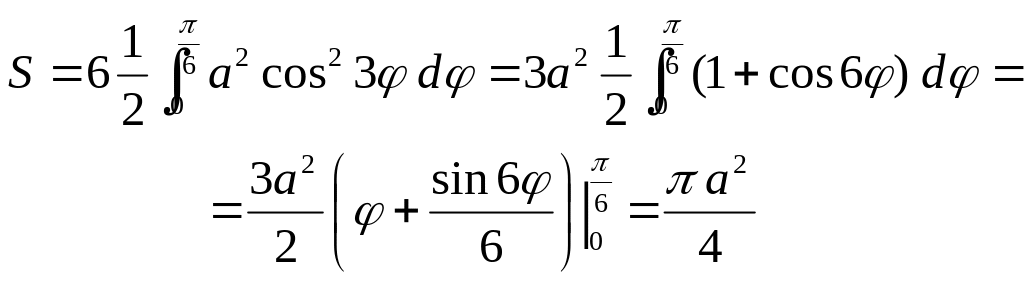
Найдем объём тела вращения, если он ограничен плоскостями х = а, х = b и поверхностью, образованной вращением кривой у = f (x).

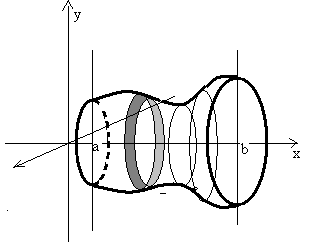
В качестве элемента интегральной суммы примем объём диска:

Переходя к пределу при , получаем следующую формулу вычисления объема тела вращения:

Пример 2. Найти объем шара радиуса R.

Решение. Вращением какой кривой описывается шар? Ответ: Вращением полуокружности. Уравнение верхней центральной полуокружности радиуса R: Отсюда получаем

Несобственные интегралы

До сих пор мы занимались вычислением интегралов на ограниченном промежутке от ограниченной функции. В некоторых случаях эти ограничения на область и на функцию можно снять. Однако, прежде чем вычислять, такие интегралы необходимо сначала исследовать на сходимость.

Интеграл называется несобственным интегралом 1 рода, если его область интегрирования неограниченна, т.е. один из пределов или оба сразу принимают бесконечные значения

Интеграл называется несобственным интегралом 2 рода, если его подынтегральная функция неограниченна, т.е. минимум или (и) максимум функции в некоторой точке промежутка интегрирования принимают бесконечные значения

Говорят, что несобственный интеграл сходится, если существует предел этого интеграла в точке разрыва подынтегральной функции или в бесконечно удалённой точке. В противном случае говорят, что несобственный интеграл расходится

Несобственный интеграл 1 рода

Это интеграл следующего вида:

или

Пример 1. Вычислить .

Решение.