Определённый интеграл и его свойства

В дальнейшем будем рассматривать определенный интеграл, построенный по схеме Римана. В отличие от неопределенного интеграла определённый интеграл от функции одной переменной с фиксированными пределами интегрирования сводится к некоторому числу

Геометрический смысл определённого интеграла

Из истории математики известно, что одной из первых задач, приведшей к понятию определенного интеграла, является задача о вычислении площади криволинейной трапеции.

Определение:

Простейшей криволинейной трапецией будем называть фигуру, ограниченную

сверху – кривой y=f(x)

снизу – осью абсцисс y=0

слева – прямой x=a

справа – прямой x=b (см. рис. 1)

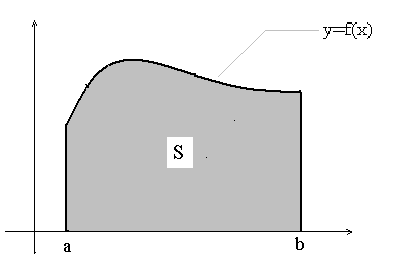
Рис. 1

1. Весь отрезок [a, b] разобьем на п частичных промежутков [x_i, х_i+1] длиной ∆x_i = x_i – х_i-1 , (i=1, 2, … , n), х₀ = a, x_п = b.

2. В каждом частичном промежутке произвольно выберем точку

3. Составим интегральную сумму

Очевидно, геометрически эта формула выражает площадь ступенчатой фигуры, составленной из прямоугольников (см. ниже рис. 2)

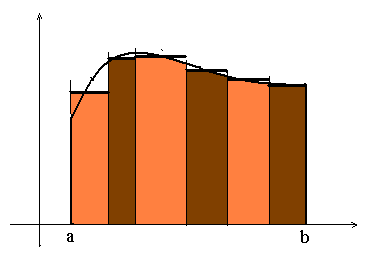
Рис. 2

4. Перейдем к пределу при п → ∞ при условии, что

(3)

При достаточно общих предположениях площадь ступенчатой фигуры стремится к площади криволинейной трапеции

Определение

Если существует конечный предел (3), то он называется определённым интегралом от функции f(х) по промежутку [a, b] и обозначается

Числа а и b называются, соответственно, нижним и верхним пределами интегрирования, а функция f(x) – интегрируемой.

Отметим, что построенный по схеме 1) – 4) интеграл называется интегралом Римана. Однако, при менее жестких ограничениях на подинтегральную функцию такой интеграл может не существовать. Тем не менее, потребности прежде всего современной физики привели к созданию интеграла Лебега, обслуживающего более широкий класс функций. В математике используются и другие конструкции интеграла

Механический смысл определённого интеграла

Если известна скорость v(t) некоторого объекта в зависимости от времени t, то с помощью интегрирования можно легко определить пройденный этим объектом путь s(t), а именно,

По аналогии, если известно ускорение a(t) некоторого объекта в зависимости от времени t, то с помощью интегрирования можно легко определить скорость движения этого объекта, а именно,

Предположим, что тело движется равноускоренно с ускорением а на временном периоде (0, t), причем в начальный момент времени скорость и путь равны нулю, т.е. a(t)=v^’(t)=a, v(0)=0, s(0)=0. Тогда

Итак, справедливы известные из школьного курса физики формулы

Ниже на графике ускорения (рис. 3) скорость тела численно равна площади заштрихованного прямоугольника

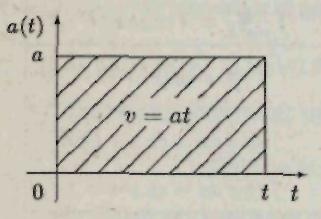
Рис. 3

Ниже на графике скорости (рис. 4) путь, пройденный телом за время (0, t), численно равен площади заштрихованного треугольника

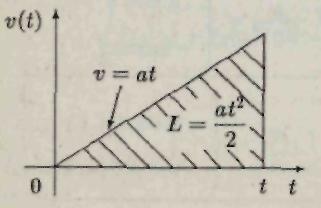
Рис. 4

Теорема Ньютона-Лейбница

Пусть функция f (х) определена, непрерывна и интегрируема на отрезке [a, b].

Определение

Интегралом с переменным верхним пределом называется интеграл следующего вида:

Здесь х – переменный верхний предел (a<x<b), t – переменная интегрирования (a<t<x). Геометрически интеграл с переменным верхним пределом означает площадь простейшей криволинейной трапеции, ограниченной справа прямой t=x. (см. рис. 5)

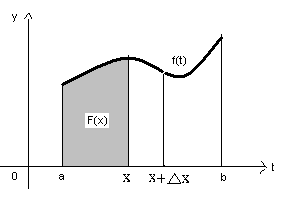
Рис. 5

Имеет место утверждение

Производная от интеграла с переменным верхним пределом равна подинтегральной функции

(4)

Доказательство. Рассмотрим приращение функции F(x) в точке х:

По определению имеем

(5)

Из рисунка 5 видно, что правую часть равенства (5) можно интерпретировать так: из трапеции aAD(x+ ) вычитается трапеция aACx. Ясно, что после вычитания остается узкая криволинейная трапеция xCD(x+ ) с основанием . Ее площадь выражается интегралом

(6)

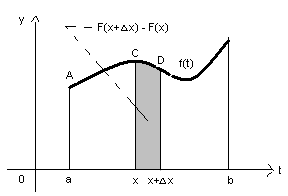
Рис. 6

По предположению функция y=f(x) непрерывна на промежутке [a, b]. Это позволяет считать, что площадь узкой криволинейной трапеции (на рис. 6 – закрашенная область) приблизительно равна площади прямоугольника с таким же основанием и высотой f(с), где . (см. рис. 7)

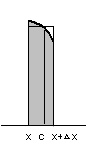
Рис. 6

Таким образом, равенство (6) можно заменить приближенным равенством

или

Переходя к пределу при , получаем

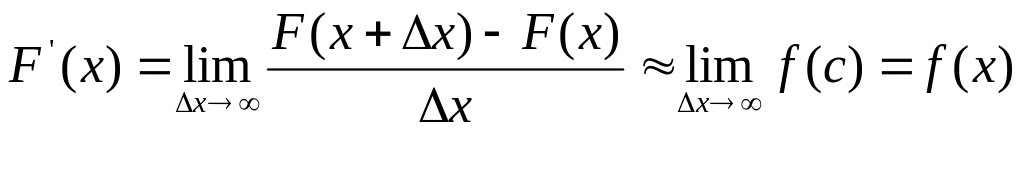
что и требовалось доказать