4. Уравнения притока жидкости к скважине

Приток жидкости в скважины происходит под действием разницы между пластовым давлением и давлением на забое скважины. Так, как движение жидкости в пласте происходит с весьма малыми скоростями, то оно подчиняется линейному закону фильтрации — закону Дарси. При постоянной толщине пласта и открытом забое скважины жидкость движется к забою по радиально-сходящвмся направлениям. В таком случае говорят о плоскорадиальной форме потока. Если скважина достаточно продолжительно работает при постоянном забойном давлении, то скорость фильтрации и давление во всех точках пласта перестает изменяться во времени и поток является установившимся.

Для установившегося плоскорадиального потока однородной жидкости по закону Дарси дебит скважины можно определить по формуле

q 2Jtkh (Рпл — Рз) ^

|iln-^£-

Г о

где Q — дебит скважины (объем жидкости, поступающей на забой скважины в единицу времени); k — проницаемость пласта; h — толщина пласта; р_пл — пластовое давление; р₃ — забойное давление в скважине; ц — вязкость жидкости; i?_K и г_с — радиусы контура питания и скважины, соответственно.

Рис. 4.3. Виды гидродинамического совершенства скважин: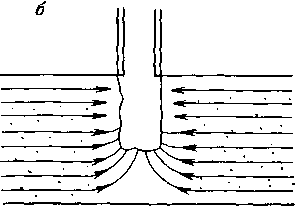

а

и ■ ,		/ ы=
——

а
		,
		.
•ж ,
. (

— совершенная скважина; 6 — несовершенная по степени вскрытия; в — несовершенная по характеру вскрытия; г — с двойным видом несовершенства

Формула (4.8), называемая формулой Дюпюи, широко используется для расчета дебита гидродинамически совершенных скважин, к которым относят скважины с открытым забоем, вскрывшие пласты на всю толщину (рис. 4.3, а).

Если скважина имеет открытый забой, но вскрыла пласт не на всю толщину (рис. 4.3,6'), то ее называют гидродинамически несовершенной по степени вскрытия. Скважины, вскрывшие пласт на всю толщину, но соединяющиеся с пластом посредством перфорации (рис. 4.3, в), являются гидродинамически несовершенными по характеру вскрытия. Есть скважины и с двойным видом несовершенства — как по степени, так и по характеру вскрытия (рис. 4.3, г).

Вблизи ствола гидродинамической несовершенной скважины происходит искажение плоскорадиальной формы потока и возникают дополнительные фильтрационные сопротивления потоку жидкости.

При расчете дебита скважин их гидродинамическое несовершенство учитывается введением в формулу Дюпюи коэффициента дополнительных фильтрационных сопротивлений С:

Q_Bc« 2я№(р_пл-рз) _ (4 9)

Величина коэффициента дополнительных фильтрационных сопротивлений зависит от степени вскрытия пласта, плотности перфорации, длины и диаметра перфорационных каналов. Обычно ее определяют, используя графики И. В. Щурова.

Формулу (4.9) можно представить с использованием понятия приведенного радиуса скважины г_{с пр}:

Q^₌2nkh(p„n-Pz)_ ' _(4Л0>

ц In ——

^ГСПР

Приведенный радиус скважины — это радиус гидродинамически совершенной скважины, которая обеспечивает при равных прочих условиях такой же дебит, как гидродинамически несовершенная скважина. Из сопоставления формул (4.9) и

10. следует, что

r_Cnv = r_ce~^c. (4.11)

Если гидродинамическое несовершенство скважины характеризовать отношением ее дебита к дебиту гидродинамически совершенной скважины в равных условиях, то

_ <?нс In (Д_к/г_с) ,, ,₀.

⁽Р~ Q -1п(Д_к/г_спр)

где ф — коэффициент гидродинамического несовершенства скважины.

Так как дебит конкретной скважины главным образом регулируется изменением депрессии на пласт, то часто используют формулу притока, записанную в виде

<2 = /(о(Рпл — Рз), (4.13)

где Ко — коэффициент продуктивности скважины.

Если фильтрация жидкости в пласте сопровождается нарушением линейного закона фильтрации, то формула притока приобретает следующий вид:

Q⁼ К® (рпл Рз)^п, (4.14)

где п — показатель степени, зависящий от условий фильтрации и составляющий 1—0,5.

В отличие от несжимаемых жидкостей, фильтрация газа в пласте сопровождается изменением его объема, а относительно высокая скорость движения газа часто делает неправомочным использование линейного закона фильтрации. Поэтому для расчета притока газа к скважинам предложен ряд формул, которые отличаются законами фильтрации и уравнениями состояния газа, положенными в их основу.

В случае установившегося притока к скважине идеального газа по линейному закону фильтрации Дарси, формула для определения дебита совершенной газовой скважины имеет вид

_{ga= (415)} ЦРа In —^JL r_c

где р_а — атмосферное давление.

При высоких скоростях движения газа (как правило в реальных условиях) расчеты, связанные с притоком газа к скважинам, основывают на двучленном законе фильтрации

-^=T^y + PP*^y2’ <^4Л6>

где р — плотность газа; — коэффициент, учитывающий структуру порового пространства и определяемый экспериментально.

Двучленный закон фильтрации в отличие от закона Дарси учитывает не только потери энергии на трение, но и на преодоление сил инерции, возникающих при движении газа (или жидкости) с большой скоростью в поровом пространстве со сложной структурой.

Формула притока идеального газа к скважине, полученная на основании закона (4.16) имеет вид

_n2 _n2 t^lPaQa Я_к I РаРаР*9о // л п \

Рая — Рз— _пм~^1П~Т- ₂ ’ ^^Л<)

где ц,—-вязкость газа; р_а — плотность газа при атмосферном давлении; Q_a — объемный дебит скважины, приведенный к атмосферному давлению; k — проницаемость пласта; h — толщина пласта; R_K — радиус контура питания; г_с — радиус скважины.

При пластовых давлениях выше 10 МПа необходимо учитывать реальные свойства газа и зависимость вязкости от давления. Если реальные свойства газа учитываются с помощью обобщенного уравнения Клапейрона — Менделеева, то формула

10. преобразуется к виду

Tp_a^z ^ In -jr~

где 7_СТ = 293,15К; Г —пластовая температура; z= (z_c-\-z„„)/2, z_c и 2_ПЛ — значения коэффициента сверхсжимаемости газа при пластовой температуре и давлениях, соответственно на забое скважины и пластовом; ц= (ц.с+|х_Пл)/2, ц._с и ^_пл— вязкость газа, соответственно в условиях забоя скважины и контура питания.

Обычно вводят обозначения

A = i£a-В= Р°^Р°^Р—. (4.19)

nkh г_с ’ 2nh*r_e ' '

Коэффициенты А и В называют коэффициентами фильтрационных сопротивлений, их использование упрощает запись формулы притока (4.17):

Р

(4.20)

²пл — P²3 = AQa + BQ²a,

Если при фильтрации по двучленному закону учитываются- реальные свойства газа, то коэффициенты фильтрационных сопротивлений определяются по следующим формулам:

27i²h²T_CTr_c

pa ^z

(4.21>

Формулы притока в виде (4.8) и (4.18) используют, как правило, в теоретических расчетах для прогноза дебита скважины, когда еще отсутствуют данные ее гидродинамических исследований, по которым можно определить /Со ипв формулах (4.13) и (4.14) или коэффициенты фильтрационных сопротивлений в формуле (4.20).

Контрольные вопросы

1. Перечислите источники пластовой энергии.

2. На что расходуется пластовая энергия?

3. Охарактеризуйте режимы работы нефтяных и газовых залежей.

4. Что понимают под коэффициентами нефте-, газо- и конденсатоотдачи пластов?

5. Запишите формулы, по которым можно рассчитать дебит нефтяной скважины.

6. Какие данные необходимы для расчета дебита газовой скважины?