8. Айналмалы қозғалыс. Бұрыштық жылдамдық жəне бұрыштық үдеу.

Шеңбер бойымен қозғалыс. Дененің шеңбер бойымен қозғалысы қисық сызықты қозғалыстың дербес жағдайы болып табылады. орын ауыстыру векторымен қатар радианмен өлшенетін бұрыштық орын ауыстыруын қарастыру ыңғайлы. Доғаның ұзындығы бұрылу бұрышымен

Δl = RΔφ.

қатынаспен байланысты.

Бұрылу бұрышы аз болған кезде Δl ≈ Δs.

1.6.1.-сурет. Дененің шеңбер бойымен сызықты және бұрыштық орын ауыстыруы.

 

Шеңбер траекториясының берілген нүктесіндегі бұрыштық жылдамдық деп кішкентай бұрыштық орын ауыстыруының кішкентай уақыт аралығына қатынасының шегін айтады.

Бұрыштық жылдамдық рад/с өлшенеді.

 Сызықтық жылдамдығы мен бұрыштық жылдамдығының арасындағы байланыс

υ = ωR.

Дененің шеңбер бойымен бірқалыпты қозғалыс кезінде υ және ω шамалары тұрақты болады. Бұл жағдайда векторының бағыты ғана өзгереді.

Дененің шеңбер бойымен бірқалыпты қозғалысы үдемелі қозғалыс болып табылады.

үдеуі шеңбер радиусы бойынша центріне бағытталады. Оны нормаль немесе центрге тартқыш үдеу деп атайды. Центрге тартқыш үдеудің модулі сызықтық υ және бұрыштық ω жылдамдықтарымен келесі қатынастармен байланысқан:

,

Осы өрнекті дәлелдеу үшін жылдамдық векторының Δt аз уақыт аралығындағы өзгерісін қарастырайық.

Үдеудің анықтамасы бойынша

А және В нүктелеріндегі жылдамдықтардың векторлары осы нүктелердегі шеңберге жүргізілген жанамалардың бойымен бағытталады. Жылдамдықтардың модульдері бірдей: υ_A = υ_B = υ.

ОАВ және ВСD үшбұрыштарының ұқсастықтарынан (1.6.2-сурет):

шығады.

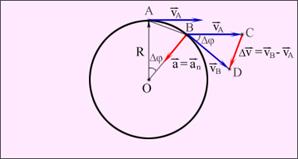1.6.2.-сурет. Дененің шеңбер бойымен бірқалыпты қозғалысы

кезіндегі центрге тартқыш үдеуі

 Δφ = ωΔt бұрышының кіші мәндерінде |AB| =Δs ≈ υΔt. |OA| = R және |CD| = Δυ болғандықтан 1.6.2.-суреттен үшбұрыштар ұқсастығынан

Δφ-дің кіші бұрыштарында векторының бағыты шеңбер центрінің бағытына жақындайды. Соның салдарынан Δt → 0 болғанда шекке көшкенде:

Дененің шеңбердегі орны ауысқан кезде шеңбер центріне бағыты өзгереді. Дененің шеңбер бойымен бірқалыпты қозғалысы кезінде үдеу модулі тұрақты қалады, бірақ үдеу векторының бағыты уақытқа байланысты өзгереді. Үдеу векторы шеңбердің кез келген нүктесінде оның центріне бағытталады. Сондықтан шеңбер бойымен түзу сызықты қозғалысы кезіндегі үдеу – центрге тартқыш үдеу деп табылады.

Центрге тартқыш үдеу векторлық формада келесі түрде жазылады:

мұндағы - басы шеңбердің центрінде орналасқан шеңбердегі нүктенің радиус-векторы.

Егер дене шеңбер бойымен бірқалыпсыз қозғалса, онда үдеудің жанама (немесе тангенциал) құраушысы пайда болады.

Бұл формулада Δυ_τ = υ₂ – υ_{1 –} жылдамдық модулінің Δt уақыт аралығындағы өзгерісі.

толық үдеу векторының бағыты шеңбер траекториясының жанама және нормаль үдеулерінің шамаларымен әр нүктеде анықталады (1.6.3.-сурет).

1.6.3.-сурет. Дененің шеңбер бойымен бірқалыпсыз

қозғалыс үдеуінің және құраушылары.

 

Дененің шеңбер бойымен қозғалысы х және у екі координатасы (жазық қозғалыс) арқылы сипаттауға болады. Дененің әр моменттегі жылдамдығын екі құраушыға υ_x және υ_y жіктеуге болады (1.6.4.-сурет).

Дененің бірқалыпты қозғалысы кезіндегі x, y, υ_x, υ_y шамалары уақыт өзгерісінде периоды

тең гармониялық заң бойынша өзгереді.

1.6.4.-сурет. жылдамдық векторының координат осьтері бойынша жіктелуі.