6. Үдеу.Үдеудің нормал жəне тангенциал құраушылары. Толық үдеу.

Дененің лездік үдеуі (немесе үдеу) деп жылдамдықтың аз өзгеруінің сол жылдамдық өзгерген уақыттың аз өзгеруіне Δt қатынасының шегін айтамыз.

Қисық сызықты қозғалыс кезінде үдеу векторының бағыты жылдамдық векторының бағытымен сәйкес келмейді. үдеу векторының құраушыларын жанама (тангенциал) және нормаль үдеу деп атайды (сурет 1.1.5).

Сурет 1.1.5. Жанама және нормаль үдеулер.

Жанама үдеу дененің жылдамдығы модуль жағынан қалай өзгеретінін көрсетеді:

векторы траекторияға жанама бойымен бағытталады.

Нормаль үдеу дененің жылдамдығы бағыты жағынан қалай өзгеретінін көрсетеді. Қисық сызықты қозғалысты шеңберлер доғаларының бойымен қозғалыс түрінде көрсетуге болады (сурет 1.1.6).

Сурет 1.1.6 Шеңберлер доғаларының бойымен қозғалыс.

Нормаль үдеу v жылдамдықтың модулінен және дене осы уақытта қозғалған шеңбердің R радиусынан тәуелді.

векторы әрқашан шеңбердің центріне бағытталады.

1.1.5. суретінен толық үдеудің модулі

шамасына тең болатыны көрініп тұр.

Сонымен, кинематикада материалдық нүктенің негізгі физикалық шамаларының қатарына: l жүрген жолы, Δs орын ауыстыруы, жылдамдық және үдеу жатады. l жолы – скаляр шама болып табылады. Δs орын ауыстыруы, жылдамдығы және үдеу – векторлық шамаларға жатады. Векторлық шаманы көрсету үшін, оның модулін және бағытын көрсету қажет. Векторлық шамалар белгілі математикалық ережелерге бағынады. Векторларды координат осьтеріне проекциялауға, оларды қосуға, алуға, т.с.с. болады.

7. Қисық сызықты қозғалыстағы жылдамдық жəне үдеу.

Егер материалдық нүкте қозғалғанда оның траекториясы қисық сызық болып келсе, онда қозғалыс қисық сызықты қозғалыс деп аталады. Енді осы қисық сызықты қозғалыс кезіндегі жылдамдықпен үдеудің өзгерісін қарастырайық.

Қисық сызықты қозғалыс кезінде жылдамдық векторы берілген әрбір уақыт мезетінде дене траекториясына қозғалыстың бағыты бойынша жүргізілген жанама бойымен бағытталады. Дененің MN қисық сызығының бойымен қозғалысын қарастырайық.(4-сурет).

Айталық M және N нүктелеріндегі қозғалыс жылдамдықтары және болсын. Ал M нүктесіндегі үдеу (1.2.9) өрнекке сәйкес мына шамаға тең.

(1.3.1) 4 – суретте көрсетілгендей бойына -ға тең және кесінділерін аламыз. Сонда үдеуді былайша өрнектейміз:

(1.3.2) (1.3.2)- өрнектің екінші құраушысы жанама немесе тангенциал үдеу деп аталады, себебі Δt→0 кезде OD кесіндісі M нүктесінің маңында айналып, траекторияның жанамасымен беттесуге ұмтылады. Оның сан мәні мынаған тең:

(1.3.3) Сонымен үдеу қозғалыс жылдамдығының сан жағынан өзгерісін көрсетеді. Кез келген бірқалыпты қозғалыс үшін болады. Ал (1.3.2)- өрнектің бірінші құраушысы нормаль немесе центрге тартқыш үдеу деп аталады, себебі Δt→0 кезде Δt→0 да, M нүктесіндегі жанамаға перпендикуляр болады. Сөйтіп, нормаль үдеудің сан мәні мына шамаға тең:

Енді ВО кесіндісінің мәні неге тең болатынын қарастырайық. ΔМВО-дан Δα бұрышын шексіз аз шама деп есептесек, ВО=MB Δα=vΔα, өйткені . Сонымен нормаль үдеуді мына түрде жазуға болады: Бұл өрнектің оң жағын Δs–ке көбейтіп және бөлейік, сонда ол түрге келеді. Мұндағы Δs – MN доғасының ұзындығы. Егер геометрия курсынан қисық сызықтың қисықтығы деген ұғымды еске алатын болсақ, онда 4-суретке сәйкес Δs=RΔα . мұндағы R-қисықтық радиусы,Δα - центрлік бұрыш. Олай болса,Δα/ Δs=1/R және M нүктесіндегі жылдамдық Δt уақыт өзгерісіне тәуелді болмайды.

Сөйтіп (1.3.4)

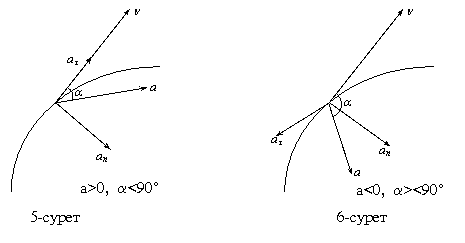
Сонымен, қисық сызықты қозғалыс кезінде нормаль үдеу қозғалыс жылдамдығы бағытының өзгерісін көрсетеді. Кез келген түзу сызықты қозғалыс үшін .(1.3.1) теңдіктен материалдық нүктенің қисық сызықты қозғалысы кезіндегі толық үдеуі оның нормаль және тангенциал үдеулері векторларының қосындысына тең екендігін көреміз: (1.3.5)Толық үдеудің бағытын тангенциал үдеу мен толық үдеу немесе нормаль үдеу мен толық үдеу арасындағы бұрыш арқылы көрсетуге болады (5,6-сурет): (1.3.6)