МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ
ФЕДЕРАЦИИ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ
ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО
ПРОФЕССИОНАЛЬНОГО ОБРАЗОВАНИЯ «ДОНСКОЙ ГОСУДАРСТВЕННЫЙ ТЕХНИЧЕСКИЙ
УНИВЕРСИТЕТ»
(ДГТУ)
Кафедра «Радиоэлектроника»
Руденко Н.В.
ЛЕКЦИЯ № 7
Резонансные явления в электрических цепях.
частотные характеристики
по дисциплине ОСНОВЫ ТЕОРИИ ЦЕПЕЙ
Ростов-на-Дону 2013 г.
ЛЕКЦИЯ № 7
Резонансные явления в электических цепях.
частотные характеристики
Учебные вопросы
1. Резонанс в последовательном колебательном контуре.
2. Частотные характеристики последовательного колебательного контура.
3. Избирательные свойства последовательного колебательного контура.
4. Резонанс в параллельном колебательном контуре.
5. Частотные характеристики параллельного контура.
Литература: [1] с.177-260.
1. Резонанс в последовательном
КОЛЕБАТЕЛЬНОМ КОНТУРЕ
Избирательные цепи или линейные узкополосные частотные фильтры это электрические цепи, которые из всей суммы колебаний различных частот пропускают на выход только колебания с относительно узкой полосой частот. Такое свойство электрической цепи называется избирательностью (селективностью).
В радиотехнике избирательные цепи применяются для выделения полезного сигнала и снижение уровня помех.
Простейшими избирательными цепями является последовательные и параллельные колебательные контуры. Избирательность колебательных контуров основана на явлении резонанса.
Резонансом называется режим электрической цепи, содержащий участки индуктивного и емкостного характера, при котором разность фаз между напряжением и током на входе цепи равна нулю.
Резонансом напряжений называется явление резонанса в участке электрической цепи, содержащей последовательно соединенные индуктивный и емкостной элемент.
1.1Условия возбуждения резонанса напряжений. Характеристики колебательного контура
Возьмем
последовательный
колебательный контур,
состоящий из последовательного соединения
индуктивного, емкостного, резистивного
элементов и источника энергии (рис.7.1,
а). Сопротивление резистивного элемента
R
включает в себя активные сопротивления
и
,
определяемые из последовательных схем
замещения соответственно катушки и
конденсатора.
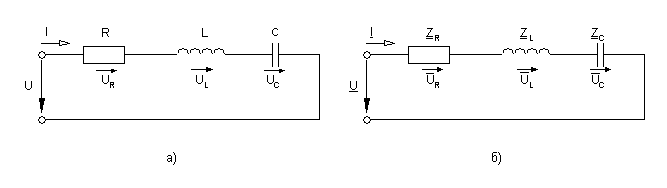
Рис. 7.1 – Схема замещения (а) и комплексная схема замещения
(б) последовательного колебательного контура
Воздействуем на контур гармоническим напряжением и проанализируем режим установившихся вынужденных колебаний. При этом целесообразно воспользоваться методом комплексных амплитуд и перейти к комплексной схеме замещения (рис.7.1, б), заменив индуктивность комплексным сопротивлением:
,
емкость – комплексным сопротивлением
,
а гармонические напряжения и ток – соответствующими комплексными действующими значениями.
Полное комплексное сопротивление колебательного контура Z равно сумме трех сопротивлений:
(7.1)
В то же время в показательной форме
,
где
– разность фаз между напряжением и
током.
Из определения
резонанса следует, что при
мнимая часть комплексного сопротивления
равна нулю:
(7.2)
Из соотношений (7.2) следует, что основным условием возбуждения резонанса напряжений в цепи гармонического тока является равенство индуктивного и емкостного сопротивления цепи:
(7.3)
Индекс «0» далее присваивается всем величинам и параметрам цепи при резонансе.
Резонансная частота цепи. Характерной особенностей резонансного режима является то, что он возникает при определенной частоте тока и напряжения, называемой резонансной частотой.
Резонансная частота есть частота тока и напряжения при резонансе в цепи.
Угловая резонансная
частота
может быть получена из соотношения
(7.2)
,
откуда
(7.4)
Как видно из формулы (4.16), эта частота определяется только параметрами цепи, поэтому она часто называется собственной частотой цепи.
При резонансе модуль реактивного сопротивления индуктивности равен модулю реактивного сопротивления емкости. Эти величины получили название характеристического волнового сопротивления ρ:
(7.5)
Из (7.5) видно, что
значение
не зависит от частоты и определяется
только параметрами реактивных элементов
контура.
Характеристическое сопротивление измеряется в Омах и является важным параметром последовательного колебательного контура.
Другим важным параметром является добротность колебательного контура Q – безразмерная величина, которая является отношением характеристического сопротивления к активному сопротивлению контура:
(7.6)
Величина обычно составляет сотни Омов (100-300 Ом), а R – единицы Омов. Поэтому добротность Q, как правило, составляет величину в несколько десятков и сотен (50-300).
Добротность контура увеличивается с уменьшением резистивного сопротивления контура и с увеличением характеристического сопротивления.
Величина, равная добротности называется затуханием контура
(7.7)
Величины , и Q являются важными характеристиками, определяющими все основные свойства последовательного колебательного контура.