4. Идеализированные пассивные элементы. Схемы замещения реальных элементов электрических цепей

4.1 Резистивный элемент

Резистивный элемент (или идеальный резистор)- это идеализированный пассивный двухполюсный элемент, в котором электрическая энергия необратимо преобразуется в другие виды энергии, например в тепловую, световую или механическую при этом запасания энергии электрического или магнитного полей в резистивном элементе не происходит.

По своим свойствам и резистивному элементу наиболее близки реальные элементы электрической цепи – резисторы, в которых электрическая энергия в основном преобразуется в тепловую. Важнейший параметр резистора, который определяет меру преобразования электрической энергии в тепловую, является его сопротивление R.

Резистивный элемент – это упрощенная модель резистора, в которой абстрагируется только его основной параметр – сопротивление.

Условное графическое изображение резистивного элемента приведено на рис. 1.5

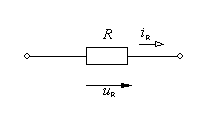
Рис. 1.5

Условные положительные направления напряжения и тока показаны стрелками. Рядом с условным графическим изображение резистивного элемента ставится его условное буквенное обозначение R.

Математическая модель элемента электрической цепи, выражающая зависимость напряжения на выводах элемента от тока в нем (или наоборот) называется уравнением данного элемента или компонентным уравнением.

Математическая модель (компонентное уравнение), описывающая свойства резистивного элемента, определяется законом Ома:

или (1.10)

Коэффициенты пропорциональности R и G в формулах (1.10) называются соответственно сопротивлением и проводимостью резистивного элемента, причем при согласованных направлениях тока и напряжения R и G положительны и связаны обратной зависимостью: R=1/G.

В системе СИ сопротивление R измеряют в Омах (Ом), а проводимость G – в сименсах (См).

Уравнение (1.10), определяещее зависимость напряжения на зажимах резистора от тока u=u(i) или тока от напряжения i=i(u) и называется вольт-амперной характеристикой (ВАХ) резистора.

Если сопротивление резистора R постоянно, по ВАХ является линейной функцией (рис. 1.6, а) и соответствует линейному резистивному элементу, причем тангенс угла наклона прямой к оси абсцисс пропорционален сопротивлению элемента: . Если же R зависит от протекающего через него тока или приложенного к нему напряжения, то ВАХ становится нелинейной функцией (рис. 1.6, б) и соответствует нелинейному резистивному элементу.

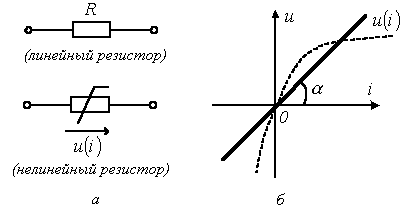
Рис. 1.6

Следует отметить, что характеристики большинства реальных резистивных элементов нелинейны: линейность – это обычно идеализация реальных ВАХ в ограниченном диапазоне токов и напряжений элемента. Так на рисунке 1.6, б качественно показана ВАХ диода, являющаяся существенно нелинейной.

Мгновенная мощность резистивного элемента может быть выражена через сопротивление R или проводимость G:

(1.11)

Мгновенная мощность резистивного элемента всегда больше нуля, так как он только потребляет энергию, преобразуя ее в тепло или другие виды энергии.

Электрическая энергия, поступающая в резистивный элемент и преобразуемая в нем в другие виды энергии, также всегда положительна (кроме случая U_R=0, i_R=0):

. (1.12)

Из (1.12) следует, что функция является неубывающей функцией времени, т.к. она вычисляется как площадь, заключенная под кривой p=p(t)>0.

Вывод

Таким образом, в любой момент времени резистивный элемент может только потреблять энергию от источников и ни в какие моменты времени он не может отдавать электрическую энергию другим элемента цепи.