1.7 Расчет элементов свободной поверхности потока
Интегрирование дифференциального уравнения движения безнапорного потока в призматических руслах с использованием зависимости дает уравнение Бахметева.
|
(1.7.1) |
где
– относительная глубина;
- Функция Бахметева, находится по таблицам в зависимости от и .
– осредненная
по участку величина, определяемая для
средней глубины
(h1
и h2
- глубины
в начальном и конечном сечениях участка,
м).
С помощью уравнения Бахметева (1.7.1) в курсовой работе решают следующие задачи:
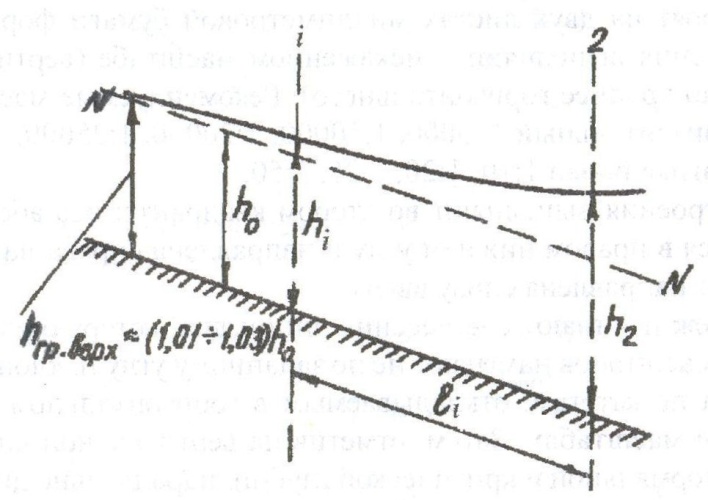
1. Для нижнего канала построить кривую свободной поверхности, и зная расстояние до перепада L, определить глубину в верхнем сечении hв3 (рисунок 1.7.1).
2. Для верхнего канала по заданному перепаду уровней Δh, определить hн1 = hвз + Δh и найти L1 - зону влияния дюкера на положение свободной поверхности.
Для построения кривой свободной поверхности по методу Бахметева уравнение (1.7.1) переписываем в следующем виде
|
(1.7.2) |
|
Рисунок 1.7.1 – Построение кривой свободной поверхности |
На основании уравнения (1.7.2) составляем таблицу по форме 1.7.1 и 1.7.2, где задаемся рядом значений глубин, начиная с известной в нижнем сечении, и вычисляем соответствующее этим глубинам расстояние от нижнего до сечения c заданной глубиной. Интервал задаваемых глубин назначаем 0,2-0,5 м, при приближении к линии нормальных глубин интервал уменьшают до 0,1 м. В верхнем граничном сечении глубина назначается так, чтобы она отличалась от нормальной на 1-3%.
Расчёты для параболического канала:
h1=hкр=0,58м
h2=h0-0,02=1,78м
=
м
Таблица 1.7.1– Расчет элементов свободной поверхности потока
hн |
η1 |
φ(η1) |
φ(η2)- φ(η1) |
1-j |
(1-j)[ φ(η2)- φ(η1)] |
η2- η1 |
Il/h0 |
L |
0,58 |
0,32 |
0,320 |
0,000 |
0,9901 |
0,000 |
0,00 |
0,000 |
0,00 |
0,73 |
0,41 |
0,412 |
-0,092 |
0,9901 |
-0,091 |
-0,09 |
0,001 |
16,36 |
0,88 |
0,49 |
0,496 |
-0,176 |
0,9901 |
-0,174 |
-0,17 |
0,004 |
65,45 |
1,03 |
0,57 |
0,582 |
-0,262 |
0,9901 |
-0,259 |
-0,25 |
0,009 |
147,27 |
1,18 |
0,66 |
0,685 |
-0,365 |
0,9901 |
-0,361 |
-0,34 |
0,021 |
343,64 |
1,33 |
0,74 |
0,789 |
-0,469 |
0,9901 |
-0,464 |
-0,42 |
0,044 |
720,00 |
1,48 |
0,82 |
0,914 |
-0,594 |
0,9901 |
-0,588 |
-0,50 |
0,088 |
1440,00 |
1,63 |
0,91 |
1,093 |
-0,773 |
0,9901 |
-0,765 |
-0,59 |
0,175 |
2863,64 |
1,78 |
0,99 |
1,682 |
-1,362 |
0,9901 |
-1,349 |
-0,67 |
0,679 |
11110,91 |
Расчеты для трапецеидального канала:
hн=1,66+0,2=1,86
h1=1,86м
h2=1,02м
=
м
Таблица 1.7.2– Расчет элементов свободной поверхности потока
hн |
η1 |
φ(η1) |
φ(η2)- φ(η1) |
1-j |
(1-j)[ φ(η2)- φ(η1)] |
η2- η1 |
Il/h0 |
L |
1,86 |
1,86 |
0,044 |
0,000 |
0,94 |
0,000 |
0,00 |
0,000 |
0,00 |
1,75 |
1,75 |
0,053 |
-0,009 |
0,94 |
-0,008 |
0,11 |
0,118 |
380,65 |
1,64 |
1,64 |
0,067 |
-0,023 |
0,94 |
-0,022 |
0,22 |
0,242 |
780,65 |
1,53 |
1,53 |
0,068 |
-0,024 |
0,94 |
-0,023 |
0,33 |
0,353 |
1138,71 |
1,42 |
1,42 |
0,112 |
-0,068 |
0,94 |
-0,064 |
0,44 |
0,504 |
1625,81 |
1,31 |
1,31 |
0,153 |
-0,109 |
0,94 |
-0,102 |
0,55 |
0,652 |
2103,23 |
1,20 |
1,20 |
0,223 |
-0,179 |
0,94 |
-0,168 |
0,66 |
0,828 |
2670,97 |
1,10 |
1,10 |
0,354 |
-0,310 |
0,94 |
-0,291 |
0,76 |
1,051 |
3390,32 |
1,02 |
1,02 |
0,706 |
-0,662 |
0,94 |
-0,622 |
0,84 |
1,462 |
4716,13 |