Б) параболическое сечение

Величина или расчетная формула	Численные значения
h, м	1,00	1,50	2,00	2,50
, м	3,58	4,38	5,06	5,66
, м2	2,39	4,38	6,75	9,43
, м	4,32	5,34	6,65	7,90
, м	0,55	0,82	1,02	1,19
, m0,5/ c	32,33	34,55	35,83	36,76
, м3/c	57,30	137,03	244,26	378,15

По данным таблицы 1.1.1(а, б) строят график зависимостей K=f(h), по которому, зная величину К₀, определяем нормальную глубину h₀ (рисунок 1.1.1, рисунок 1.1.2).

Для трапецеидального сечения:

h0, м	ω0, м2	, м	, м	, м0,5/с	K0, м3/с
1,00	3,30	5,41	0,61	46,05	118,69

Для параболического сечения:

h0, м	B0, м	ω0, м2	, м	, м	, м0,5/с	K0, м3/с
1,80	4,80	5,76	6,13	0,94	35,35	197,41

Для проверки вычисляем модуль расхода, соответствующий найденной нормальной глубине, и рассчитываем погрешность по формуле

(1.1.5)

Расчет считают завершенным, если Δ_K < 5%.

Для трапецеидального сечения:

Принимаем h₀ = 1,00 м.

Для параболического сечения:

Принимаем h₀ = 1,80 м.

1.2 Расчет критической глубины потока

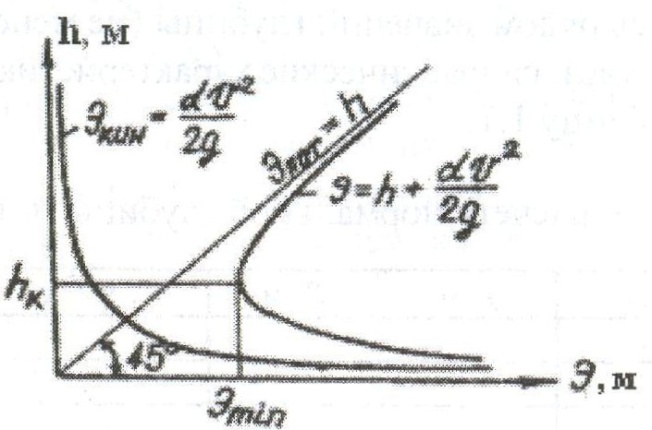
Критическая глубина h_к — это глубина, соответствующая мини­муму удельной энергии сечения (рисунок 1.2.1). Индекс «к» в даль­нейшем будет означать, что характеристика соответствует крити­ческой глубине.

Для определения критической глубины графическим способом сначала вычисляем постоянную величину , затем задаем ряд значений глубины (не менее 4) и находим геометрические характеристики сечения.

Для трапецеидального сечения

Для параболического сечения

Рисунок 1.2.1 – График удельной энергии сечения

Расчет сводим в таблицу 1.2.1 (а, б).

Таблица 1.2.1 - К расчету критической глубины потока

а) для трапецеидального сечения

Величина или расчетная формула	Численные значения
h, м	1,00	0,60	0,50
В=b+2mh, м	4,80	3,60	3,30
ω=(b+mh)h, м2	3,30	1,62	1,28
	7,47	1,18	0,63

б) для параболического сечения

Величина или расчетная формула	Численные значения
h, м	1,00	0,80	0,40
В, м	3,58	3,20	2,27
ω=2/3Bh, м2	2,39	1,71	0,61
	3,81	1,56	0,09

По данным таблицы 1.2.1 строим график зависимости , на нем откладываем найденное ранее значение Δ_к, по которому определяем критическую глубину h_к (рисунок 1.2.2, рисунок 1.2.3).

Для трапецеидального сечения:

hк, м	ωк, м2	, м	B, м		, м0,5/с
0,45	1,11	3,42	3,15	0,32	41,35	0,43

Для параболического сечения:

hк, м	Bк, м	ωк, м2	, м		, м0,5/с
0,58	2,72	1,05	3,05	0,34	29,84	0,43

Принимаем для трапецеидального сечения h_к = 0,45 м.

Принимаем для параболического сечения h_к = 0,58 м.

1.3 Расчет критического уклона канала

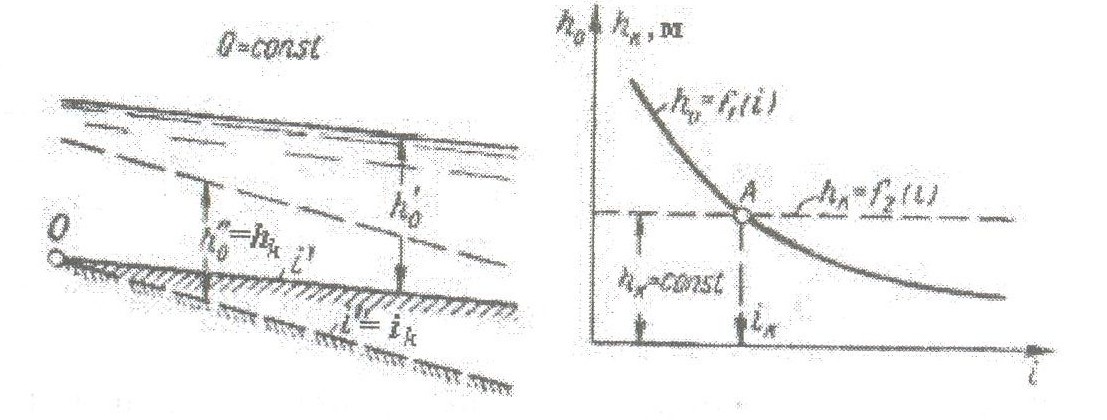
Критический уклон i - воображаемый уклон, который надо придать рассматриваемому призматическому руслу, чтобы при заданном расходе Q и при равномерном движении воды в русле нормальная глубина h₀ оказалась равной критической h_K (рисунок 1.3.1).

Критический уклон рассчитываем по формуле

	(1.3.1)
Для трапецеидального сечения критический уклон равен Для параболического сечения критический уклон равен
Рисунок 1.3.1 – К определению критического уклона

В трапецеидальном сечении h₀ > h_к, i < i_к, значит поток при равномерном движении будет находиться в спокойном состоянии.

В параболическом сечении h₀ > h_к, i < i_к, значит поток при равномерном движении будет находиться в спокойном состоянии.