4.4 Расчет прочности ригеля по сечениям, наклонным к продольной оси

Э пюра поперечных сил:

Рис. 16. Эпюра поперечных сил

Для левого ригеля V_{sd max}=218,908 кН.

Согласно п.6.2.3. ТКП EN 1992-1-1-2009 для элементов с вертикальной поперечной арматурой сопротивление срезу принимается как меньшее из значений:

где A_sw — площадь сечения поперечной арматуры;

s — расстояние между хомутами;

f_ywd — расчетное значение предела текучести поперечной арматуры;

₁ — коэффициент понижения прочности бетона, учитывающий влияние наклонных трещин;

_cw — коэффициент, учитывающий уровень напряжения в сжатом поясе (принимаем равным единице);

z=0,9d – плечо внутренней пары сил;

=40⁰ – угол между трещиной и продольной осью плиты;

- коэффициент для учета неравномерности распределения напряжений в арматуре по высоте сечения (принимается равным 0,8);

=0,528 (f_ck в МПа)

Принимаем поперечную арматуру 3 16 класса S240 ( ).

Определим шаг арматуры s:

=

Окончательно принимаем шаг поперечной арматуры на приопорных участках левого ригеля:

S₁=200мм

Уточним значение :

Таким образом, при данной арматуре:

< и > , где = 282, 226кН.

Значит, подобранная арматура удовлетворяет условиям прочности.

Принимаем на приопорных участках поперечную арматуру 3 16 S240 c шагом s₁=200мм. В середине пролёта шаг принимается s₂=400мм при арматуре того же класса и диаметра, т.к. согл. п. 9.2.2(6) ТКП EN, наибольшее продольное расстояние между следующими друг за другом элементами поперечной арматуры не должно превышать значения s_l,max, где:

Определим коэффициент поперечного армирования для приопорного участка(форм.9.4 ТКП EN):

,

где _w — коэффициент поперечного армирования; _w должен быть не менее _w,min;

A_sw — площадь сечения поперечной арматуры на длине s ( );

S — расстояние между поперечной арматурой, измеренное вдоль продольной оси элемента (шаг поперечной арматуры); для приопорного участка ;

b_w — ширина ребра элемента ( );

 — угол между поперечной арматурой и продольной осью элемента;

равен 90⁰

Тогда:

То же для середины пролета (s₂=400мм):

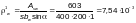
Определим минимальный коэффициент армирования (форм. 9.5N ТКП EN):

Расчётный процент поперечного армирования превышает минимально требуемый.

Для правого ригеля V_{sd max}=241,708 кН.

Принимаем поперечную арматуру 3 14 класса S240 ( ).

Определим шаг арматуры s:

=

Окончательно принимаем шаг поперечной арматуры на приопорных участках левого ригеля:

S₁=200мм

Уточним значение :

Таким образом, при данной арматуре :

< и > , где = 241, 708кН.

Значит, подобранная арматура удовлетворяет условиям прочности.

Окончательно принимаем на приопорных участках поперечную арматуру 3 14 S240 c шагом s₁=200мм. В середине пролёта шаг принимается s₂=400мм при арматуре того же класса и диаметра, т.к. согл. п. 9.2.2(6) ТКП EN, наибольшее продольное расстояние между следующими друг за другом элементами поперечной арматуры не должно превышать значения s_l,max, где:

Определим коэффициент поперечного армирования для приопорного участка(форм.9.4 ТКП EN):

,

где _w — коэффициент поперечного армирования; _w должен быть не менее _w,min;

A_sw — площадь сечения поперечной арматуры на длине s ( );

S — расстояние между поперечной арматурой, измеренное вдоль продольной оси элемента (шаг поперечной арматуры); для приопорного участка ;

b_w — ширина ребра элемента ( );

 — угол между поперечной арматурой и продольной осью элемента;

равен 90⁰

Тогда:

То же для середины пролета (s₂=400мм):

Определим минимальный коэффициент армирования (форм. 9.5N ТКП EN):

Расчётный процент поперечного армирования превышает минимально требуемый.