4.2 Вычисление изгибающих моментов в расчетных сечениях ригеля
Опорные и пролетные моменты вычисляют в программном комплексе “RADUGA-BETA”
Различные схемы загружения постоянной и временной нагрузкой приведены в табл.3.
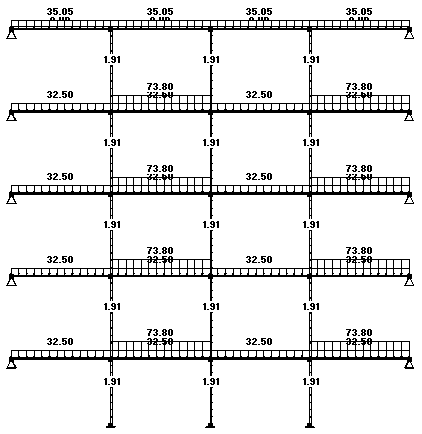
Рисунок 2 Схема нумерации стержней и узлов:
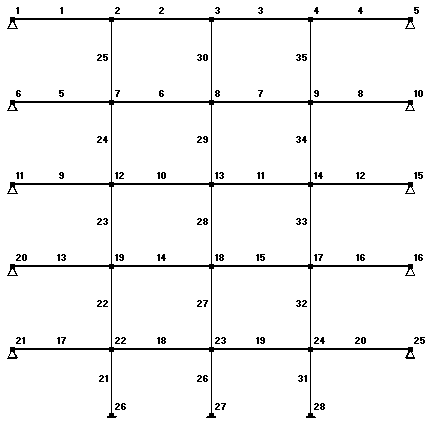
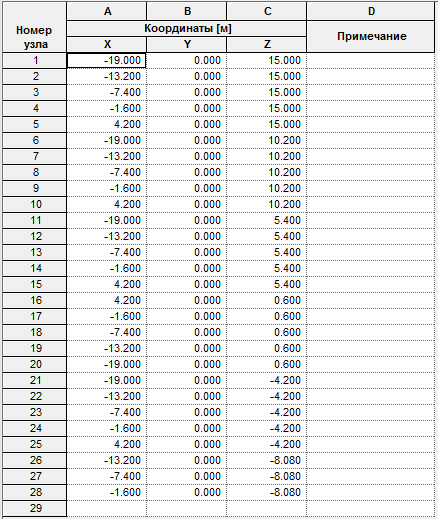
Таблица 2 Координаты узлов рамы
Схемы загружения ригелей.
Схема 1 ( ВН1-постоянная нагрузка) Схема 2 ( ВН2-снеговая нагрузка)
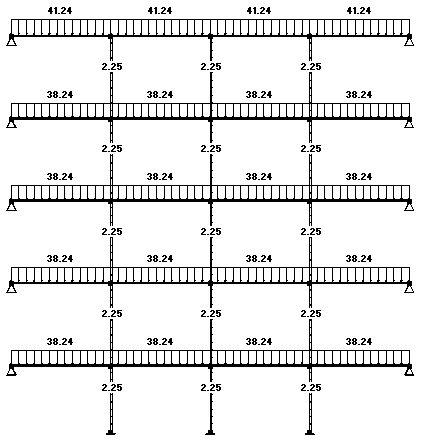
Схема 3 ( ВН3-временная 1) Схема 4 (ВН4-временная 2)
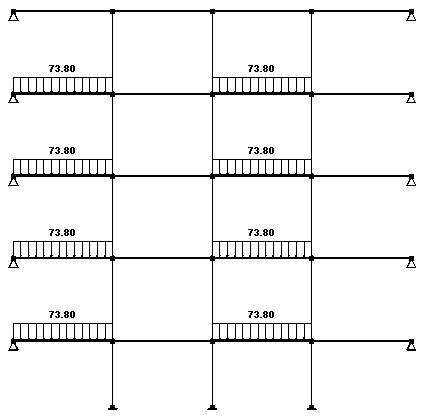
Схема 5 ( ВН5-временная 3)
Комбинация 1(Постоянная +Временная 1)
Комбинация 2 (Постоянная +Временная 2)
Комбинация 3 (Постоянная +Временная 3)
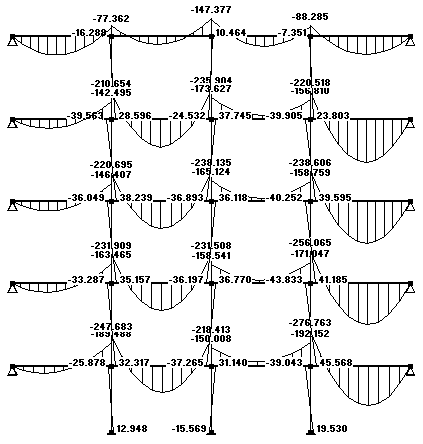
4.3 Перераспределение моментов под влиянием образования пластических шарниров в ригеле.
Рассмотрим участки ригеля, которые подвержены наибольшим изгибающим усилиям.
Схема нагружения: постоянная + снеговая + временная 1
Схема нагружения: постоянная + снеговая + временная 2
Схема нагружения: постоянная + снеговая + временная 3
Здесь ВН – вариант нагружения, КН – комбинация нагружений, общий эффект которых в одной комбинации вычисляется по формуле:
,
Где
- эффект воздействия;
- расчётное
значение постоянной нагрузки;
-
расчётное значение снеговой нагрузки;
-
расчётное значение временной нагрузки
(является преобладающей);
- коэффициент сочетания для снеговой нагрузки (для РБ принимается 0,7);
- понижающий коэффициент.
Для данной расчетной схемы приняты следующие варианты нагружений:
ВН1 – постоянная нагрузка от собственного веса элементов конструкций;
ВН2 – снеговая нагрузка;
ВН3 – временная нагрузка первых двух пролетов и далее через один;
ВН4 – временя нагрузка через один междуэтажный пролёт, начиная с крайнего левого;
ВН5 – временная нагрузка через один междуэтажный пролёт, начиная со второго.
В соответствии с принятыми вариантами нагружений, образуем следующие комбинации нагружений:
1) КН1=0,85ВН1+0,7ВН2+ВН3;
2) КН2=0,85ВН1+0,7ВН2+ВН4;
3) КН3=0,85ВН1+0,7ВН2+ВН5;
4) КН4=0,85ВН1+0,7ВН2+ВН6;
Для двух крайних ригелей второго этажа строим огибающие эпюры изгибающих моментов, а также эпюры изгибающих моментов после перераспределения внутренних усилий вследствие образования пластических шарниров в опорных сечениях с наибольшим по абсолютному значению опорным моментом:
