4.2.2. Материальный, тепловой балансы и кинетические закономерности абсорбции

Материальный баланс процесса выражается общим уравнением

,

отсюда общий расход абсорбента

,

а его удельный расход

. (4.34)

Это уравнение можно переписать следующим образом:

. (4.35)

Уравнение (4.35) показывает, что изменение концентрации в абсорбционном аппарате происходит прямолинейно и, следовательно, в координатах рабочая линия процесса абсорбции представляет собой прямую линию с углом наклона, тангенс которого равен .

Между удельным расходом абсорбента и размерами аппарата существует определенная связь. Через точку с координатами и (рис. 4.9) проведем в соответствие с уравнением (4.35) рабочие линии ВА, ВА₁, ВА₂, ВА₃, отвечающие разным удельным расходам абсорбента. При этом точки А, А₁, А₂, А₃ будут лежать на одной горизонтальной прямой, соответствующей заданной начальной концентрации газа в смеси .

Рабочая линия ВА, совпадающая с вертикалью, соответствует максимальной движущей силе процесса, однако удельный расход абсорбента в этом случая будет бесконечно большим ( ). Если же рабочая линия ВА₃ касается линии равновесия, то удельный расход абсорбента - минимален ( . Движущая сила в точке касания рабочей равновесной линий равна нулю, в ней рабочая концентрация становится равной равновесной. При бесконечно большом расходе адсорбента размеры аппарата будут наименьшими, при минимальном расходе – бесконечно большими. Следует отметить, что оба случая являются предельными и практически неосуществимыми.

Рис.4.9. К определению удельного расхода абсорбента.

В реальном абсорбере равновесие между фазами не достигается и всегда , где - концентрация поглощаемого газа в жидкости, находящейся в равновесии с поступающим газом. Отсюда следует, что величина всегда быть больше минимального значения , отвечающего предельному положению рабочей линии (ВА₃). Значения удельного минимального расхода абсорбента можно определить по формуле:

(4.36)

Значение является отправной величиной для установления действительного расхода абсорбента при расчете и проектировании абсорберов. Действительный расход абсорбента должен быть больше минимального и равен оптимальному его значению, которое можно установить в результате технико-экономического расчета. В предварительных расчетах можно принимать

.

При растворении газа в жидкости температура жидкости обычно повышается вследствие выделения тепла. Если абсорбция ведется без отвода тепла, то можно допустить, что все выделяющееся тепло идет на нагревание жидкости.

Количество тепла, выделяющегося при абсорбции для определенного сечения аппарата, может быть найдено по уравнению

.

Температура абсорбента при подводе тепла повышается на величину

,

где q – дифференциальная теплота растворения газа; с – теплоемкость раствора.

Тогда изменение температуры абсорбента по длине (высоте) абсорбера может быть вычислено по зависимости:

.

Задаваясь рядом произвольных значений в интервале между известными концентрациями и , по вышеприведенной зависимости вычисляют температуру абсорбента. По опытным данным определяются соответствующие значения равновесных концентраций и строят линию равновесия (по точкам О₁ , О₂ и т.д , рис. 4.10.).

Кинетические закономерности абсорбции соответствуют общему уравнению массопередачи для двухфазных систем:

; .

В этих уравнениях движущую силу часто заменяют разностью парциальных давлений распределяемого компонента , а на . Тогда

; .

При таком способе выражения концентрации уравнение для равновесной зависимости имеет вид

.

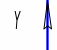
Рис.4.10. Кривая равновесия при неизотермической абсорбции.

Соответственно коэффициенты массопередачи выражаются в виде:

; (4.37)

. (4.38)

Чем выше растворимость газа, тем больше значение величины . Для плохо растворимых газов имеет наименьшее значение. Величина влияет на структуру уравнений, описывающих коэффициент массопередачи. Если велико, то в уравнении (4.37) величина . Тогда можно считать , т.е. в данном случае диффузионное сопротивление сосредоточено в газовой фазе. Если мало, то в уравнении (4.38) , и можно полагать , т.е. в этом случае сопротивление сосредоточено в жидкой фазе.

Коэффициенты массопередачи по жидкой и газовой фазам рассчитываются по критериальным уравнениям, полученным на основании теории подобия. Такие уравнения обычно представляются в виде:

.

Постоянные коэффициенты устанавливаются при обработке экспериментальных данных.

При расчете абсорбции для случая, когда жидкость стекает по стенке тонкой пленкой, а газ соприкасается с абсорбентом по поверхности этой пленки, коэффициент массоотдачи для газовой фазы может быть рассчитан по формуле:

,

где ; ; .

Зависимость справедлива для 100-10000 и 0,5 – 2,0.

Для жидкой пленки в насадочных колоннах критериальная зависимость имеет вид

.