5.Проверка на устойчивость исходной сау по критерию Гурвица

Из пункта 3 получили характеристический полином:

Для того, что бы составить определитель Гурвица надо по диагонали от левого верхнего до правого нижнего элемента матрицы выписать все коэффициенты. Пустые строки заполняем так, чтобы чередовались строки с нечетными и четными индексами и, если коэффициент отсутствует, то на его месте пишем 0. Строим определитель Гурвица:

По определению САУ устойчива, если определитель Гурвица и все его диагональные миноры положительны:

Отсюда следует, что замкнутая САУ является неустойчивой.

По Найквисту:

Годограф АФЧХ охватывает точку с координатами (-1;0) и движется по часовой стрелке, поэтому по критерию Найквиста САУ неустойчива.

6.Моделирование переходных характеристик исходной сау

С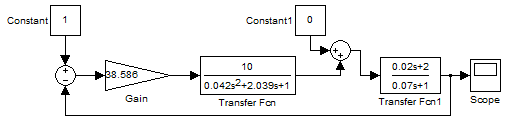 труктурная схема для моделирования в MatLab представлена на рис.14.

Рис.14. Схема исходной САУ в MatLab

Здесь g не изменяется и равно своему минимальному значению 1, возмущающее воздействие z тоже равно своему минимальному значению 0.

Результат моделирования представлен на рис.15.

Рис.15. Результат моделирования при

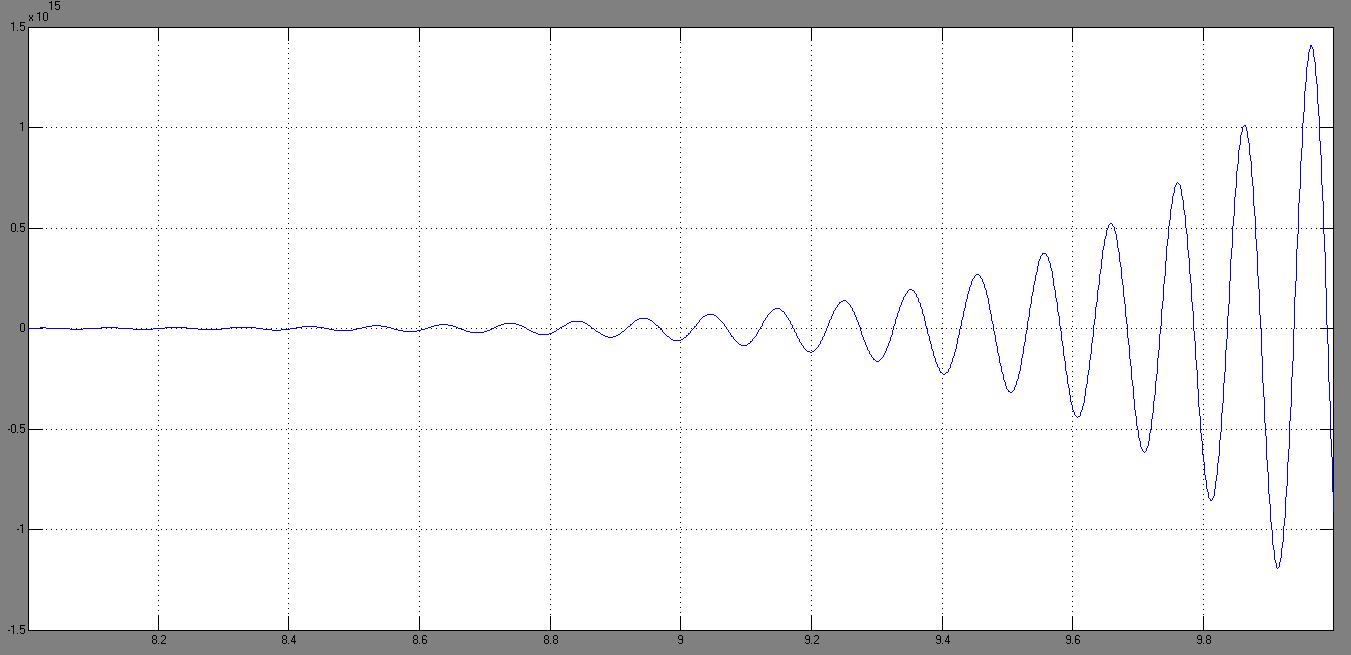
Рис.16. Результат моделирования при

Рис.15.1. Увеличенный результат моделирования при

САУ неустойчива, колебания происходят с нарастающей амплитудой.

Период колебаний:

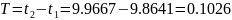
Частота колебаний:

Коэффициент расхождения:

Декремент расхождения:

Как видим, частота рад/c, коэффициент расхождения , логарифмический декремент расхождения 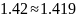приблизительно равны с рассчитанными в п.3, этим мы доказываем правильность выполненных расчётов.

7.Синтез корректирующего устройства, обеспечивающего настройку исходной системы на симметричный оптимум.

Рис.17. Структурная схема скорректированной САУ

Желаемая передаточная функция разомкнутой системы, настроенной на симметричный оптимум, имеет вид:

где 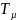-наименьшая постоянная времени нескорректированной системы

Передаточная функция разомкнутой САУ имеет вид:

Определим коэффициент демпфирования:

;

За принимаем минимальное из постоянных времени интегрирования нескорректированной системы, т.е. . Значит, желаемая передаточная функция будет выглядеть следующим образом:

Обозначив как передаточную функцию корректирующего устройства (регулятора) и определив передаточную функцию разомкнутой системы , можно отыскать следующим образом:

Регулятор включает в себя:

• Два пропорционально-интегрирующего звена:

• Инерционное дифференцирующее звено со статизмом:

7.1. Синтез регулятора упрощённой сау, обеспечивающей настройку исходной системы на симметричный оптимум.

Для упрощения передаточной функции САУ и понижения ее порядка пренебрегаем малыми постоянными времени, не оказывающими существенного влияния на частотные характеристики САУ:

так как постоянные времени форсирующего звена первого порядка (0,01p+1)и инерционного звена первого порядка малы, товлиянием этих звеньев можно пренебречь:

За принимаем минимальное из постоянных времени интегрирования нескорректированной системы, т.е. .Значит желаемая передаточная функция будет выглядеть следующим образом:

Передаточная функция упрощенного корректирующего устройства:

Упрощенный регулятор включает в себя два пропорционально- интегрирующих звена: