6.7. Непрерывность функции

Понятие непрерывности функции, так же как и понятие пре­дела, является одним из основных понятий математического ана­лиза.

Определение 1. Функция Дх) называется непрерывной в точке

(6.22)

х₀, если она удовлетворяет следующим трем условиям: 1) определе­на в точке л:₀ (т.е. существует Дх₀)); 2) имеет конечный предел функции при х->х₀ ; 3) этот предел равен значению функции в точ­ке х^, т.е.

lim /(*) =

л- ->х_п

₂

г)

О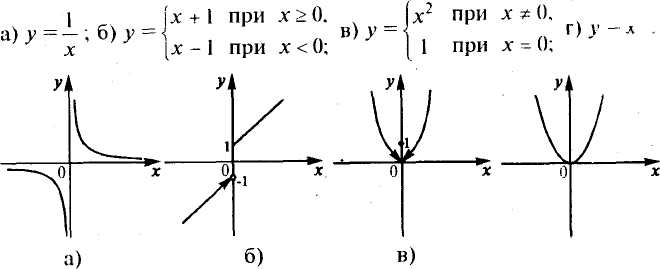 Пример 6.6. Исследовать непрерывность в точке х=0 задан­ных функций:

Рис. 6Л

Решение, а) В точке х = 0 функция у =/(х) (см. рис. 6.7а) не является непрерывной, так как нарушено первое условие не­прерывности — существование /(0).

160

6 Высшая математика для экономистов

161

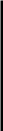б) В точке х = 0 функция у - Дх) (см. рис. 6.76) не является непрерывной — первое условие непрерывности выполнено, ДО) существует (ДО) = 1), но нарушено второе условие — отсутствует lim/(x) (точнее говоря, здесь существуют односторонние преде-

лы функции слева lim /(*)=-1 и справа lim /(х)=1, но обще-

го предела при х-»0 не существует).

в) В точке х = 0 функция у = Дх) (см. рис. 6.7в) не является непрерывной — первые два условия непрерывности выполнены — существуют/(0) (ДО) =1) и конечный предел lim/(x)=0, но

дг->0

нарушено третье основное условие: lim f(x) *Д0).

г) В точке х = 0 функция у = Дх) (см. рис. 6.7г) непрерывна, так как выполнены все три условия непрерывности — lim /(x) =

х-->0

=Д0)=0>

Определение непрерывности функции (6.22) в точке х₀ может

быть записано и так:

lim /(*) = /(lim х), (6.23)

Уо+АУ

т.е. для непрерывной функции возможна перестановка символов предела и функции.

Рис. 6.8

Очевидно, что непрерывность функции в данной точке выра­жается непрерывностью ее графика при прохождении данной точки (без отрыва карандаша от листа бумаги).

Сформулируем еще одно, второе определение непрерывности.

Дадим аргументу х₀ приращение Дх. Тогда функция у=Дх) по­лучит приращение Ду, определяемое как разность наращенного и исходного значения функции: Ду=Дх₀ + Дх)-Дх₀) (см.рис.6.8).

Определение 2. Функция у = Дх) называется непрерывной в точке х₀, если она определена в этой точке и бесконечно малому

приращению аргумента соответствует бесконечно малое прираще­ние функции:

(6.24)

lim Ду= 0.

Дх->0

□ Убедимся в равносильности двух приведенных определений непрерывности. Из первого определения согласно (6.22) при х=х_о+Дх следует lim /(х₀ + Лх) =/(х₀), так как стремление

Лх->0

х-> х₀ равносильно условию Дх-»0.

На основании теоремы о связи бесконечно малых величин с пределами функций можно записать /(хд + Дх) = /(хо) + а(Лх), где а(Дх) =/(хо + Дх)-/(хо)=Ду есть бесконечно малая при Дх-»0, т.е. lim Ay = 0 .■

Точка х₀ называется точкой разрыва функции Дх), если эта

функция в данной точке не является непрерывной. Различают точки разрыва: первого рода (когда существуют конечные одно­сторонние пределы функции слева и справа при х-»х₀, не рав­ные друг другу) и второго рода (когда хотя бы один из односто­ронних пределов слева или справа равен бесконечности или не существует). Так, точка х_о= 0 на рис. 6.76 — точка разрыва пер­вого рода, а на рис.6.7а — точка разрыва второго рода. К точкам разрыва первого рода относятся также точки устранимого разры­ва, когда предел функции при х-»х₀ существует, но не равен

значению функции в этой точке. Так, точка х_о= 0 на рис. 6.7в

является точкой устранимого разрыва. Свойства функций, непрерывных в точке:

1. Если функции fix) и ф(х) непрерывны в точке х₀, то их сумма

/(*) _Ф(х)

{при условии

Дх)+ф(х), произведение Дх)ср(х) и частное

ф(х₀ )*0) являются функциями, непрерывными в точке х₀.

162

163

Рис. 6.10

Доказательство теоремы следует из определения непрерывно­сти и аналогичных свойств пределов функций.

2. Если функция у = Дх) непрерывна в точке х₀ и Дх_о)>(), то

существует такая окрестность точки х₀, в которойДх)>0.

Доказательство этого свойства основывается на том, что при малых приращениях аргумента Дх->0 в соответствии со вторым определением непрерывности функции (6.24) можно получить как угодно малое приращение функции Ду, так что знак функции у=Дх) в окрестности (х₀—Дх, х_о+Дх) не изменится.

3. Если функция y—f(u) непрерывна в точке щ,, а функция и=ц>(х) непрерывна в точке uq =^р(х₀), то сложная функция у⁼/[ц>(х)] не­ прерывна в точке х₀.

Доказательство состоит в том, что малому приращению аргу­мента Ах->0 в силу второго определения непрерывности (6.24) функции и=ц>(х) соответствует как угодно малое приращение Ди-Я), приводящее в свою очередь в силу того же определения непрерывности функции y—f{u) к как угодно малому прираще­нию Ау->0.

Свойство 3 может быть записано в виде

lim /[<р(х)] = / Hm <р(х) ,

т.е. под знаком непрерывной функции можно переходить к пределу.

Функция у = Дх) называется непрерывной на промежутке X, если она непрерывна в каждой точке этого промежутка. Можно доказать, что все элементарные функции непрерывны в области их определения.

[>Пример 6.7. Доказать непрерывность функции y=cas x. Решение. Найдем lim Ay = lim (cos(x + Ax) - cos x) =

Л*->0 Дд:~>0

2x + Ax . Ax

= 2 lim cos

Лх->0

(6.251

2x + дх

cos-

sin — =0, так как

.. .Ax 1 .. fsm(Ax/2) _A \ 1 .. sin(Ax/2) .. _A hm sin — = - lim — . ■ Ax = - hm —^-r— hm Ax =

2 2 \ /2 ) 2 А2

Ах/2

= — •1-0 = 0, т.е. lim Ay=0, и по второму определению непре-

2 ДЛГ-+О

рывности (6.24) функция .y=cos x является непрерывной на всей числовой ^

Замечание. Еще раз подчеркнем, что непрерывность функции в любой точке области определения гарантируется лишь для элементарных функций. Рассмотрим в качестве примера функцию Дх) = [х] (читается "у равно антье х"), где [х] — целая часть числа х, т.е. наибольшее целое число, не превосходящее х

(например, [2,6] = 2, [-2,6] =-3). В точке х =- функция Дх)=

=[х] непрерывна, ибо lim/(х) = / — =1, а в точке х = 1 эта

функция определена — Д1) = 1, но терпит разрыв, ибо lim/(x)

не существует (точнее существуют неравные между собой конеч­ные пределы функции слева lim /(x) =0 и справа lim /(x)=l)

х\0 10

(см.рис.6.9). У,

\-0

У=[х)

3" 2-!■

Это связано с тем, что Дх)= =[х] не является элементарной функцией, и, хотя и определена на всей числовой прямой, раз­рывна во всех целых точках.

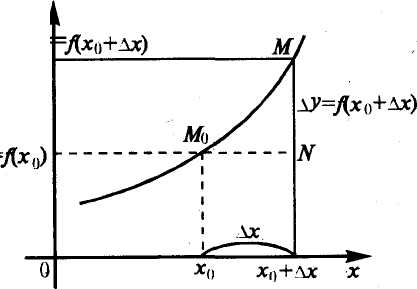
Свойства функций, непрерыв­ных на отрезке:

1. Если функция у = Дх) не-

-1°

~ТН 1 I !-"► прерывна на отрезке [я, Ь], то

~2 ^ ^она ограничена на этом отрезке

Рис. 6.9 (см. рис. 6.10).

Рис. 6.11

2. Если функция у = Дх) не­прерывна на отрезке [а, Ь], то она достигает на этом отрезке наименьшего значения т и наибольшего значения М (теорема Вей-ерштрасса) (см.рис. 6.11).

164

165