8.2. Правило Лопиталя

Теорема. Предел отношения двух бесконечно малых или беско­нечно больших функций равен пределу отношения их производных {конечному или бесконечному), если последний существует в указан­ном смысле.

Итак, если имеется неопределенность вида | — |или | — |, то

^ГТ- (8-3)

g(x)

П Рассмотрим доказательство теоремы для неопределенности

го"|

вида - прих->х₀.

Для простоты будем предполагать, что функции Дх) и g(x), a

также их производные непрерывны в точке х₀, причем lim f(x) =

х->х₀

)=0 и lim £(x) = £(x_o)=O.

В этом случае lim

_^4 ^Ш _{^1^ч •}

g(x) x->x₀ g(x) - g(X₀)

Применяя теорему Лагранжа для функций fix) и g(x) на отрез­ке [х, х₀], получим

g(x) где х < %\ < xq , х < ^2 < ^хо •

При х-»х₀ в силу непрерывности производных f'(x) и g'(x) имеем /'(Si )->/'(х₀) и #'( 12 )-►£'(•*<))• Используя теорему о пределе частного двух функций, получаем равенство (8.3).и

Замечание. Обращаем внимание, что в правой части формулы (8.3) берется отношение производных, а не производная отношения.

[> Пример 8.1. Найти:

... х _.. ,. х* , ,. log_ax а) шп —; б) lim —; в) lim °° .

Р е ш е н и е. а) Имеем неопределенность вида — . Приме-

L°°J няя правило Лопиталя, получим:

х'

lim— =

= lim

оо | *->«. (_е^ху

б) Имеем также неопределенность вида — . Применим пра-

[_ooj

вило Лопиталя [к]+1 раз, где [к] — целая часть числа t

loo]

= - =hm

*->» _a^x _ш² д

Шп*1 = |-1=Ит

i^x In a I oo к{к-\)..\к-\к\)х

— 1X111

При каждом применении правила Лопиталя степень числите­ля будет уменьшаться на единицу и через [к]+1 раз станет отри­цательной, т.е. числитель обратится в бесконечно малую величи­ну (если к — не целое число; если к — целое, то в постоянную величину). Знаменатель же будет оставаться бесконечно большой

х^к

величиной. Таким образом, lim —т- =0.

*->■*> а

_ч ,. log₀x Гоо] (log.x)' ,.

в) шп ^Ьа, = — =hm ^{v Ьа}, ' = шп л;-»» х |_оо J х-^со (х )' х-+«

fcx^K

——шп—_г=0> kina х-><*> х

( )

х" .. а^х

= «, lim — = oo.

log_fl х *->» х

Правило Лопиталя дает возможность сравнения бесконечно больших величин: степенная функция х"~ бесконечно большая более высокого порядка, чем логарифмическая log_a x , а показа­тельная а^х — бесконечно большая более высокого порядка, чем

степенная х"; это означает, что lim [> Пример 8.2. Найти:

_е^х + _е^х _ 2 a) lim 5 ; б) lim x In x.

Р е ш е н и е. а)

<,*+<,-*_ 2 ГО] .. (<?^X+<T lim = ⁼ х ⁼ и¹¹¹ i

О

2x

•2)' .. -^- = lim

Неопределенность вида I — I по-прежнему сохраняется. При-

меним правило Лопиталя еще раз:

О' „,

■=1.

,. е^х-е^х .. (е^х lim —i = шп

2х х4Ь (2х)' х^Ь 2 б) Имеем неопределенность вида [Ооо]. Переписывая данное выражение в виде

lim (x In x) =[0-oo]= lim —— , получим неопределенность ви-

lim ^ = [-1= lim -^- = lim(-x)=0.^

x->0+ 1 [_ooj x->0+ 1 x->0

x "x²"

Правило Лопиталя является эффективным методом раскрытия неопределенностей. Однако применение его не всегда приводит к цели. О Пример 8.3. Найти:

_ч .. VxTT _сч ,. x + sinx a) lim , ; б) lim —.

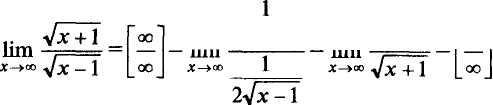
_ ..•_ 2Vx + l _ „„ Vx-1 _

Р е ш е н и е. а) Если применить правило Лопиталя, то полу­чим

т.е. числитель и знаменатель просто меняются местами; неопре­деленность же сохраняется. Если применить правило Лопиталя вторично, то функция под знаком предела примет первоначаль­ный вид. Таким образом, применение этого правила в данном случае не позволяет раскрыть неопределенность. В то же время легко установить, что

lim

■= lim

x-¥«> ijx — 1 x->°°

/x + 1

б) Если применить правило Лопиталя, т.е.

COSX

. . x + sinx Гоо] (x + sinx)' .. 1 + шп = — =шп^ ^-=шп —

COSX

x->ooX-SinX L°°J *-*°° \^х "■^{sm Х}У x-xol-

то можно сделать ошибочный вывод о том, что предел данной функции не существует, так как не существует lim cos x.

smx

x + sin x

= 1,

smx

1 На самом деле lim = lim

I: x-»°o x - sin x

1-

да| — |. Применяя правило Лопиталя, получим

00

sinx

так как lim

X->°o X

=0 (см. пример 6.8в)>-