
- •3. Матрицалар және оларға амалдар қолдану. Мысал.Матрица және олардың түрлері
- •5. Аналитикалық геометрияның қарапайым есептері (екі нүктенің арақашықтығы; берілген кесіндіні белгілі қатынаста бөлу). Екі нуктенін ара қашықтығы
- •6. Векторлар және оларға қолданылатын сызықтық амалдар. Екі вектордың скалярлық көбейтіндісі. Вектор және оған амалдар қолдану
- •2Вектордың скаляр көбейтіндісі
- •9.Туынды ұғымы, геометриялық және физикалық мағынасы. Функция туындысы
- •10.Кері және күрделі функциясының туындысы. Мысалдар. Күрделі функция туындысы
- •13. Функцияның экстремумы. Экстремумның қажетті және жеткілікті шарттары.Функция экстремумы
- •Егер х аргумент х0 нүкте арқылы өткенде таңбасын оңнан теріске өзгертсе, онда х0 нүкте функцияның максимум нүктесі болады;
- •Егер х аргумент х0 нүкте арқылы өткенде таңбасын терістен оңға өзгертсе, онда х0 нүкте функцияның минимум нүктесі болады;
- •Егер х аргумент х0 нүкте арқылы өткенде таңбасын өзгертпесе, онда х0 нүкте функцияның экстремум нүктесі емес.
- •Егер болса, онда х0 нүкте f(X) функциясының максимум нүктесі болады;
- •Егер болса, онда х0 нүкте f(X) функциясының минимум нүктесі болады.
- •14. Функция графигінің дөңес және ойыстығы, иілу нүктелері. Асимптоталар.Қисықтың дөңестігі, ойыстығы, иілуі
- •18. Анықталған интеграл және оның қасиеттері. Ньютон-Лейбниц формуласы.Анықталған интеграл
- •20. Екі айнымалы функциялар, негізгі ұғымдар. Дербес туындылар және толық дифференциал. Дербес туындының толық диференциялы
- •21. Бірінші ретті дифференциалдық теңдеулердің негізгі түрлері және оларды шығару тәсілдері. Мысал. 1-ші ретті сызықты біртекті диф.
- •22.Анықталған интеграл көмегімен жазық фигураның ауданын, доғаның ұзындығын, айналу денесінің көлемін есептеу Жазық фигураның ауданын табу.
- •3. Қисық доғасының ұзындығы
- •Дифференциалды есептеу формулаларын келтірейік:
- •24.Түзулердің параллельдік және перпендикулярлық шарттары
- •25.. Шегін есепте.
9.Туынды ұғымы, геометриялық және физикалық мағынасы. Функция туындысы
Көп жағдайда функция мәнін білумен қатар аргументтің өзгерісіне байланысты функцияның өзгеру жылдамдығын білу де маңызды болады.
y=f(x)
функциясын
қарастырайық (1-сурет).
Осы функция
![]() кесіндісінде анықталған және үзіліссіз
болсын. Кез келген
кесіндісінде анықталған және үзіліссіз
болсын. Кез келген
![]() үшін
үшін
![]() айырма х
аргументтің
нүктесіндегі өсімшесі
деп
аталады да,
айырма х
аргументтің
нүктесіндегі өсімшесі
деп
аталады да,
![]() деп белгіленеді. Сонымен,
=
деп белгіленеді. Сонымен,
=![]() x
=
+
.Ал
x
=
+
.Ал
![]() айырма f(x)
функциясының
нүктесіндегі өсімшесі
деп
аталады да,
айырма f(x)
функциясының
нүктесіндегі өсімшесі
деп
аталады да,
![]() деп белгіленеді. Сонымен,
деп белгіленеді. Сонымен,
![]() =
=
=
=![]() .
.
2-суретте
көрсетілген y=f1(x)
және
y=f2(x)
функцияларды
қарастырайық. Аргумент мәні
![]() шамаға өзгергенде бұл функциялардың
мәндері де белгілі бір шамаға өзгереді.
Суретте f2(x)
функцияның
мәні f1(x)
функцияға қарағанда көп өзгереді
(өседі).
шамаға өзгергенде бұл функциялардың
мәндері де белгілі бір шамаға өзгереді.
Суретте f2(x)
функцияның
мәні f1(x)
функцияға қарағанда көп өзгереді
(өседі).
Аргумент мәні бірдей шамаға өзгерген кездегі функциялардың өзгерістерін салыстыру үшін функцияның өзгеріс жылдамдығы ұғымын енгізеді. Оны орташа жылдамдық дейді де, функция өзгерісінің аргумент өзгерісіне қатынасымен анықтайды:
Орташа жылдамдық |
= |
Функция өзгерісі |
|
|
Аргумент өзгерісі |
= |
|
Орташа
жылдамдық х0
нүктесіне ғана қатысты қарастырылмай,
аргумент өзгерісінен де байланысты
болады. Функция жылдамдығын аргумент
өзгерісінен байланыссыз қарастыру үшін
функцияның нүктедегі жылдамдығын
қарастырады. Функцияның нүктедегі
жылдамдығын анықтау үшін х-ті
х0
аргументке
шексіз жақындатады, немесе
![]() .
Осы кезде үзіліссіз функция өзгерісі
нолге жақындайды, яғни
.
Осы кезде үзіліссіз функция өзгерісі
нолге жақындайды, яғни
![]() .
Нолге шексіз жақындайтын функция
өзгерісінің нолге шексіз жақындайтын
аргумент өзгерісіне қатынасы функцияның
х0нүктедегі
өзгеріс жылдамдығын береді. Функцияның
х0нүктедегі
осы өзгеріс жылдамдығын f(x)
функциясының
х0нүктедегі
туындысы деп атайды:
.
Нолге шексіз жақындайтын функция
өзгерісінің нолге шексіз жақындайтын
аргумент өзгерісіне қатынасы функцияның
х0нүктедегі
өзгеріс жылдамдығын береді. Функцияның
х0нүктедегі
осы өзгеріс жылдамдығын f(x)
функциясының
х0нүктедегі
туындысы деп атайды:![]() .
.
Анықтама.Функция
өсімшесінің аргумент өсімшесіне
қатынасының аргумент өсімшесі нолге
ұмтылған кездегі шегі функция
туындысы
деп аталады. Әдетте оны
![]() немесе
немесе
![]() деп белгілейді:
деп белгілейді:
![]()
.Туындының
геометриялық мағынасы:
![]() туындысы
туындысы
![]() функциясының графигіне
функциясының графигіне
![]() нүктесінде жүргізілген жанаманың
бұрыштық коэффициенті болады. Осы
жанаманың теңдеуін былай жазады:
нүктесінде жүргізілген жанаманың
бұрыштық коэффициенті болады. Осы
жанаманың теңдеуін былай жазады:
![]() .Туындының
механикалық мағынасы. Егер
.Туындының
механикалық мағынасы. Егер
![]() айнымалысын
уақыт деп есептеп,
айнымалысын
уақыт деп есептеп,
![]()
функциясы дененің жүрген жолын сипаттаса,
онда
функциясы дененің жүрген жолын сипаттаса,
онда
![]() дененің
уақытындағы
жылдамдығын білдіреді.
дененің
уақытындағы
жылдамдығын білдіреді.
10.Кері және күрделі функциясының туындысы. Мысалдар. Күрделі функция туындысы
f(u(x))
күрделі
функция туындысы:
![]() .
.
u=g(x) дифференциалданатын функция болсын. Сонда
-
№№
y=f(x)
y=f(u(x))
1
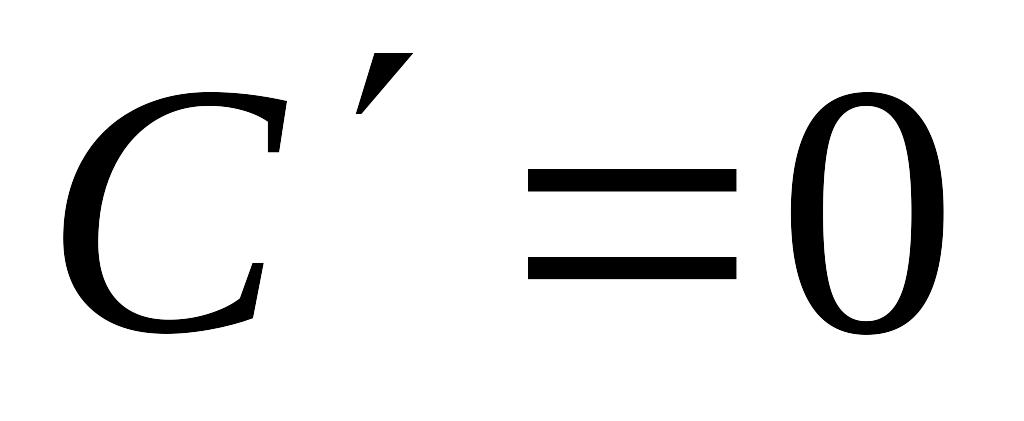
2
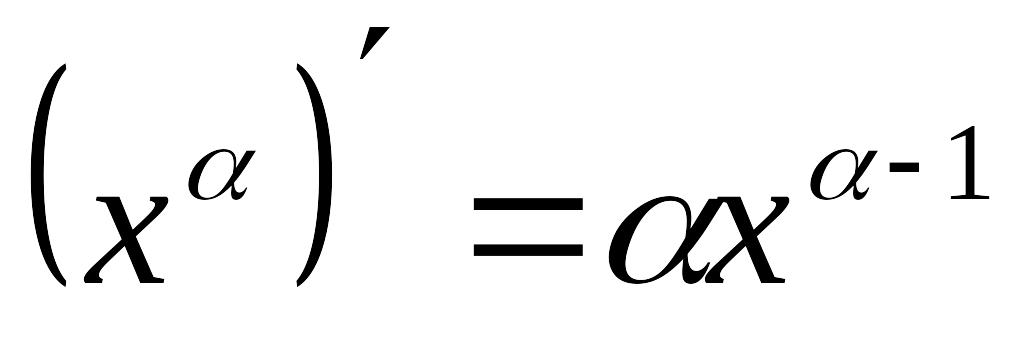
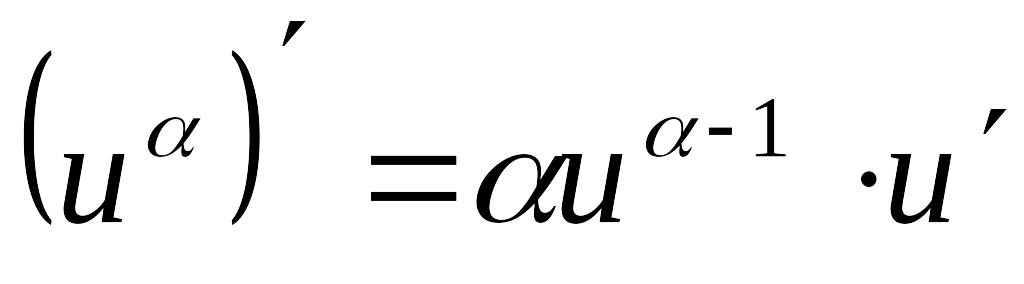
3
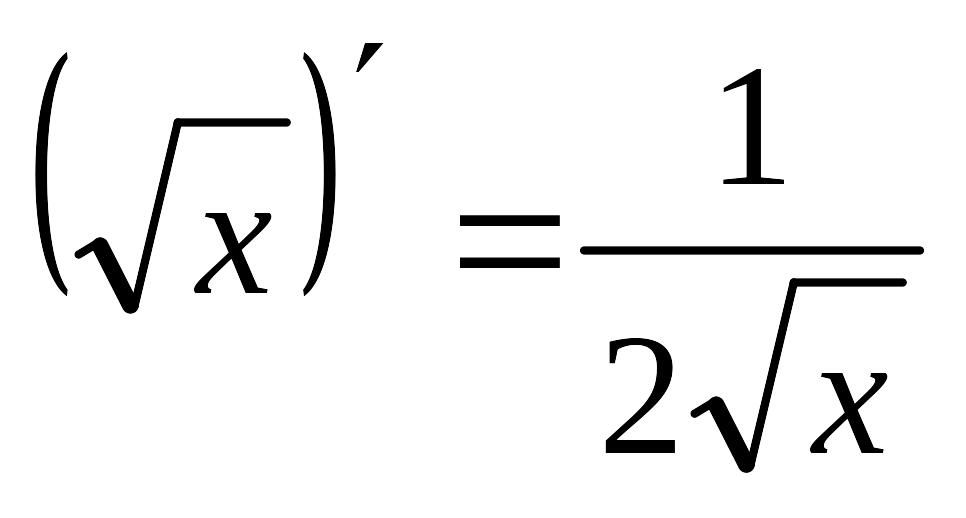


4
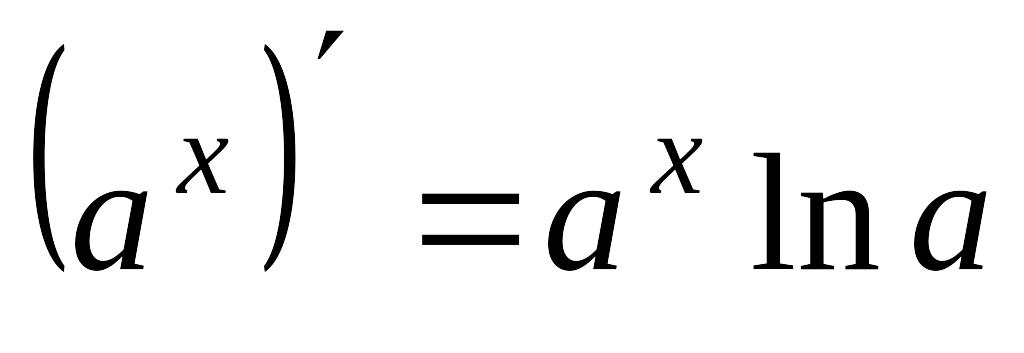 ,
0<a
,
0<a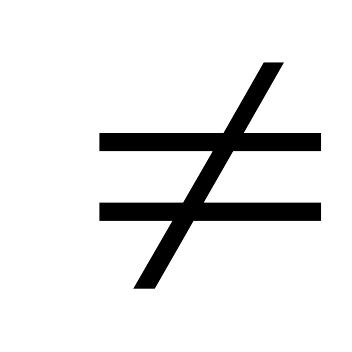 1
1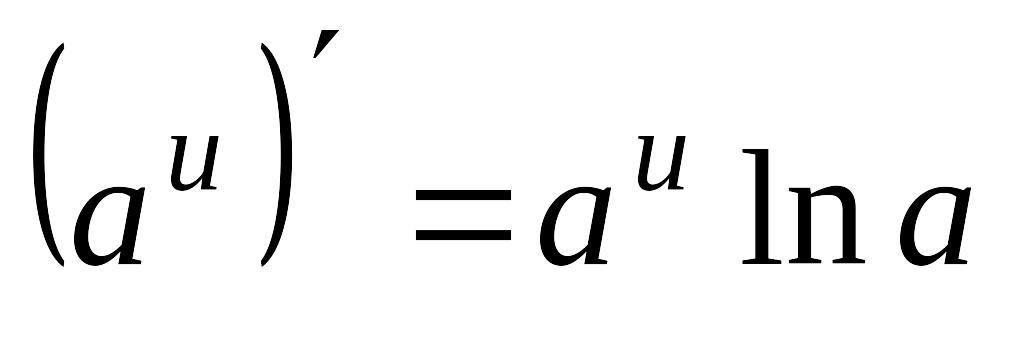
5
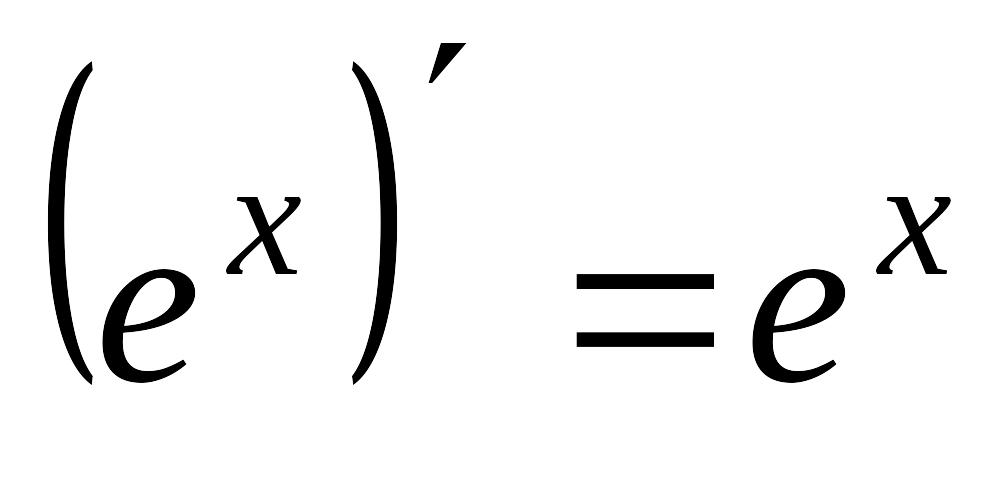
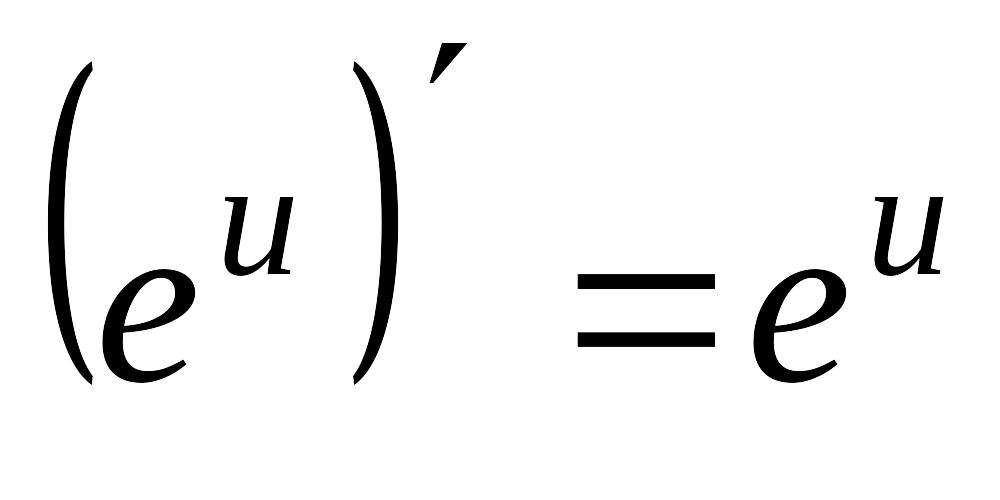
6
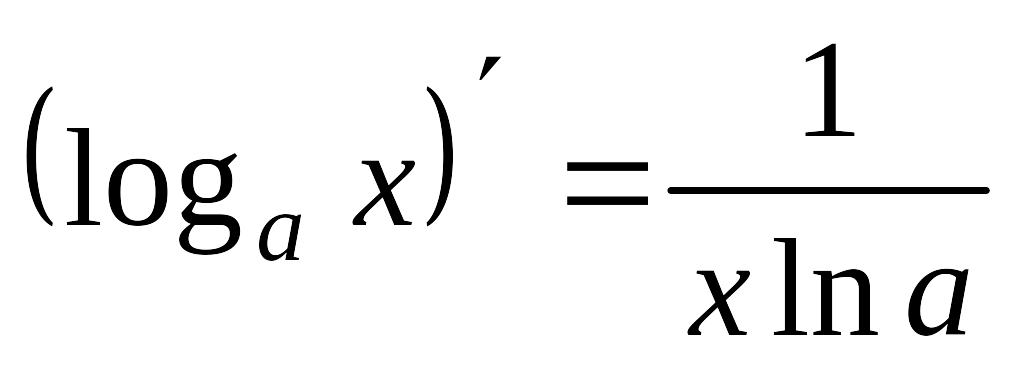 ,
0<a
1
,
0<a
1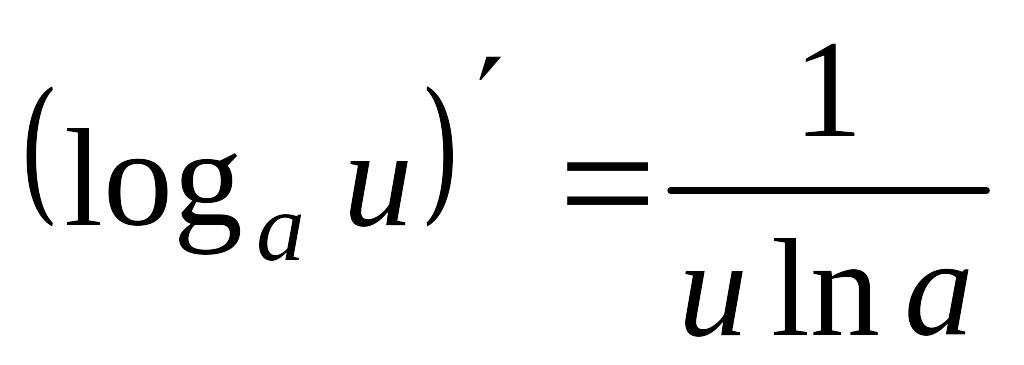
7
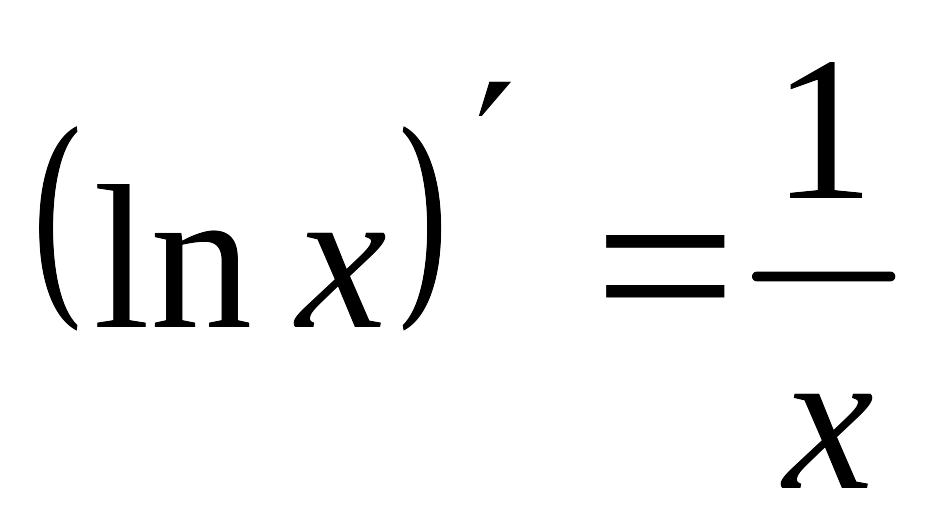
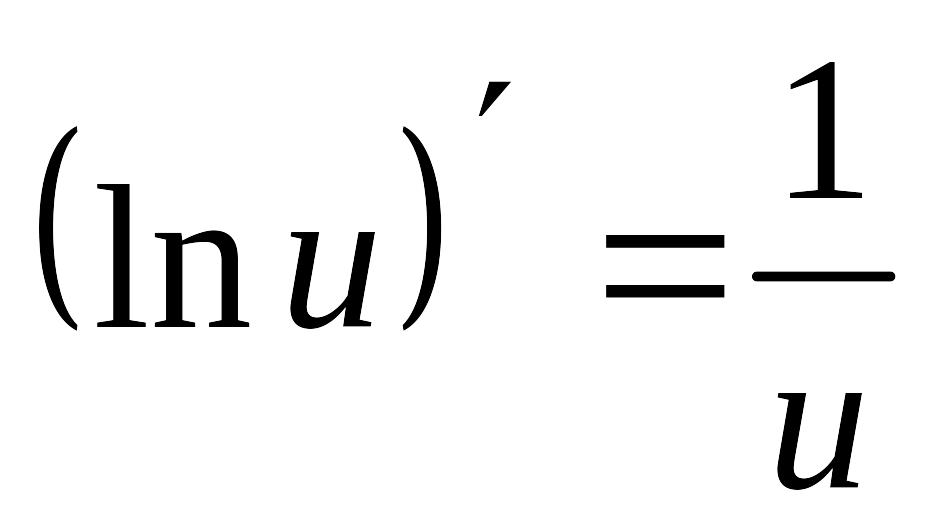
8
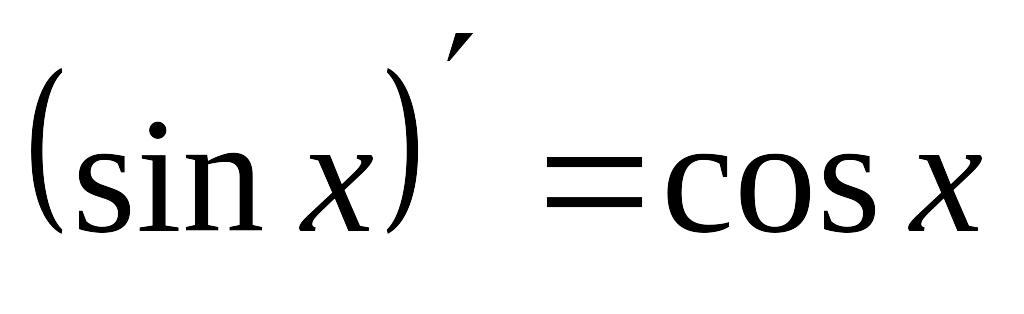
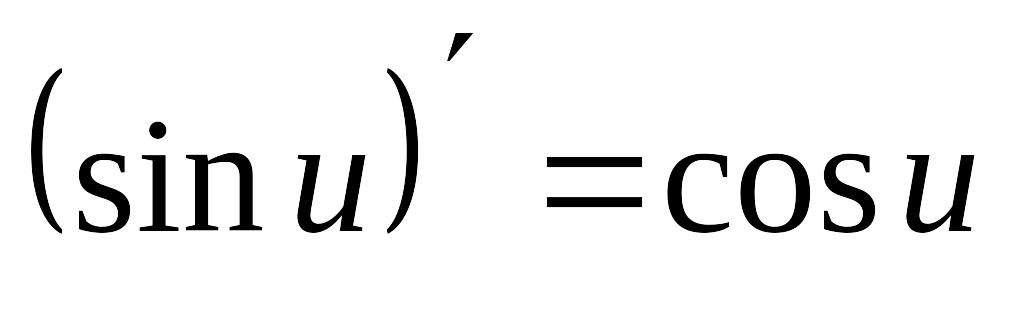
9


10
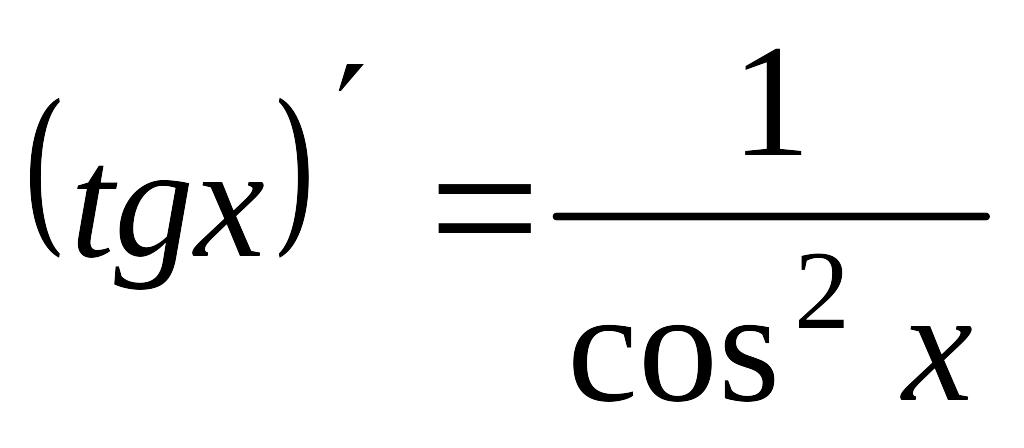
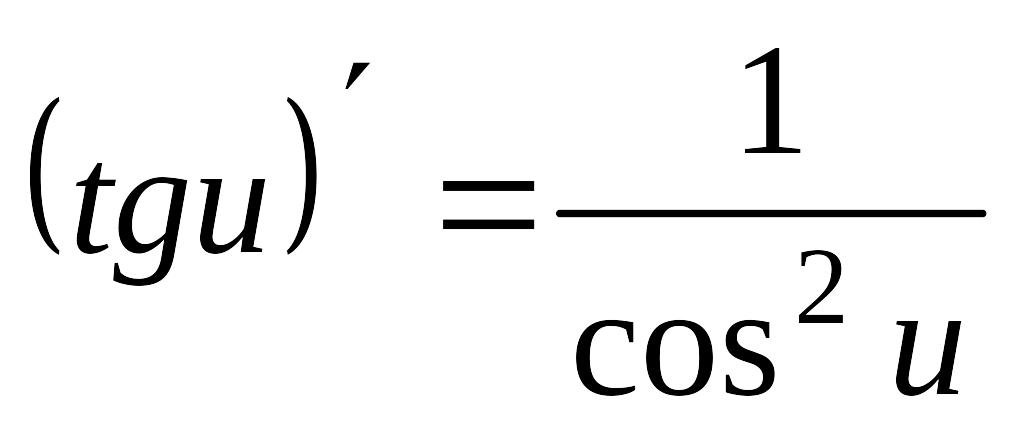
11
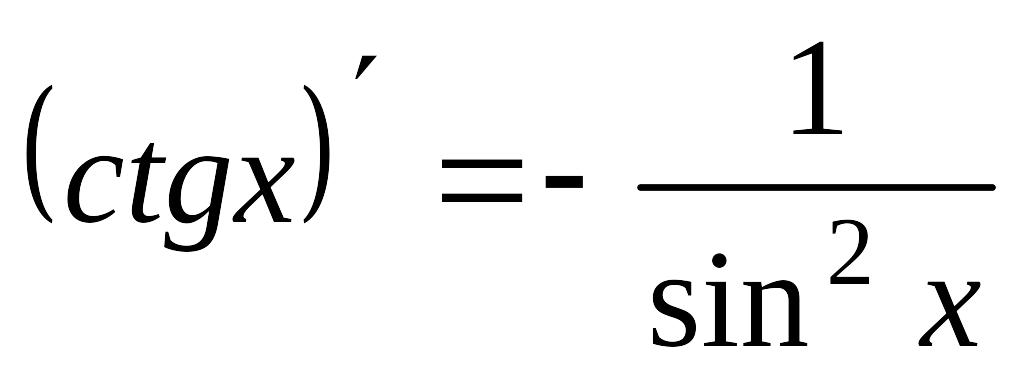
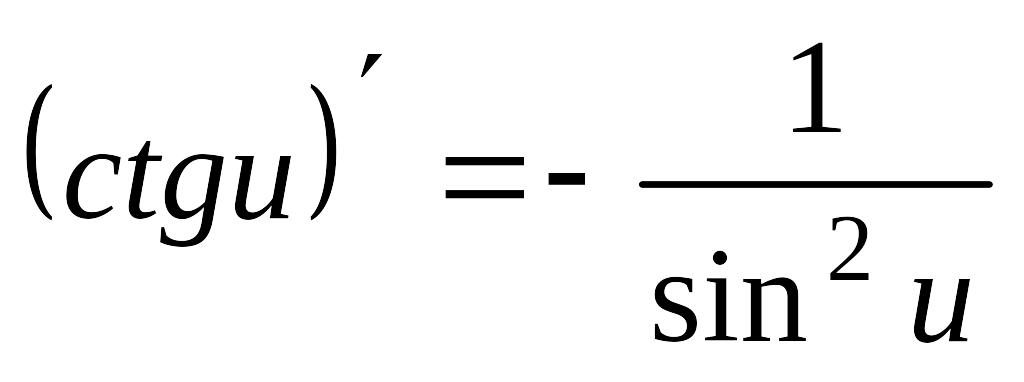
12
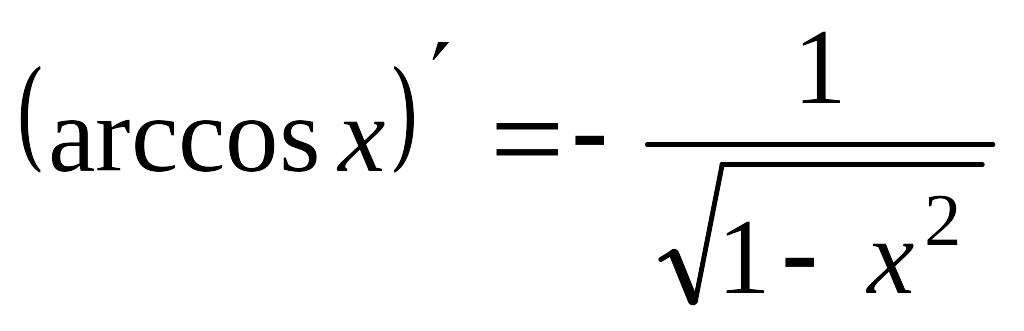
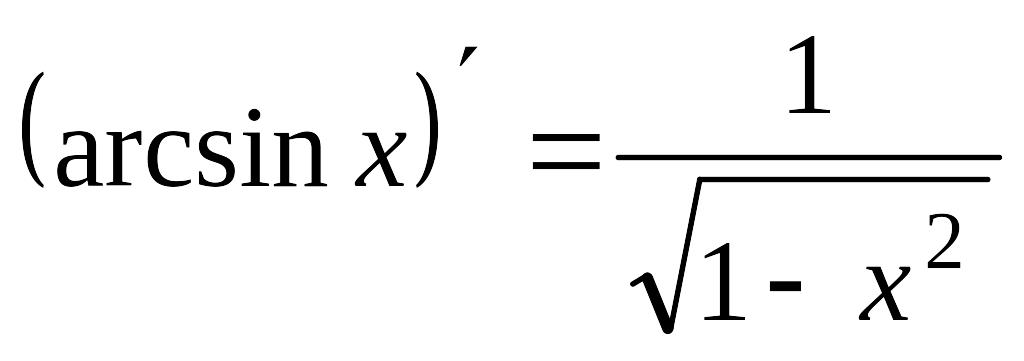

13
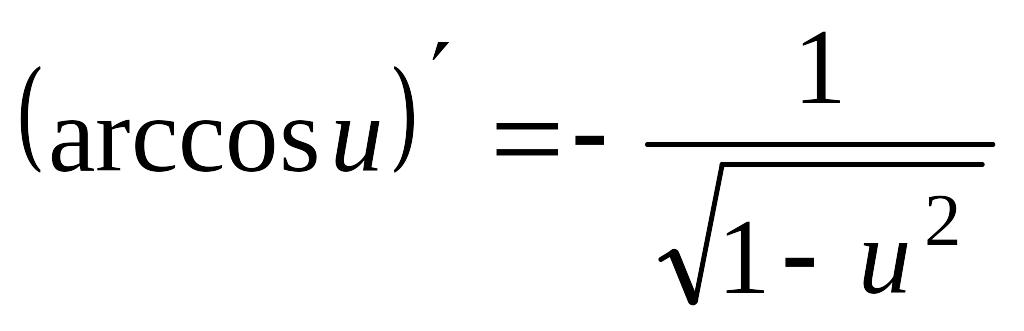
14

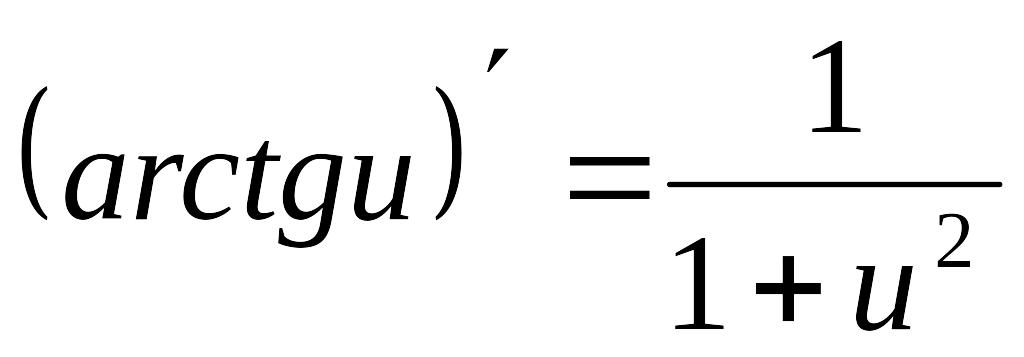
15
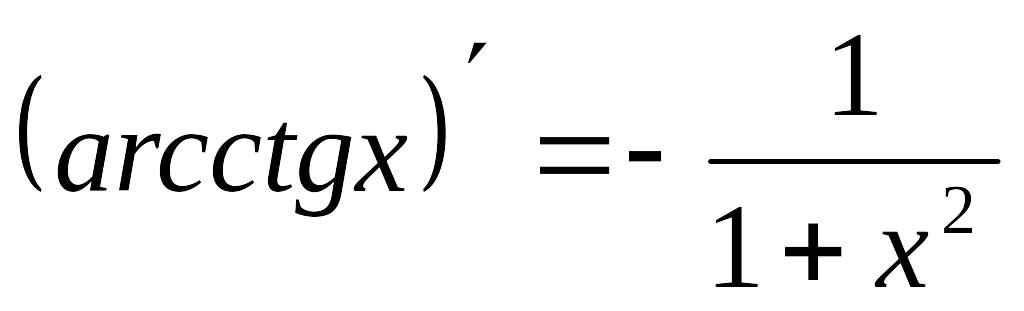
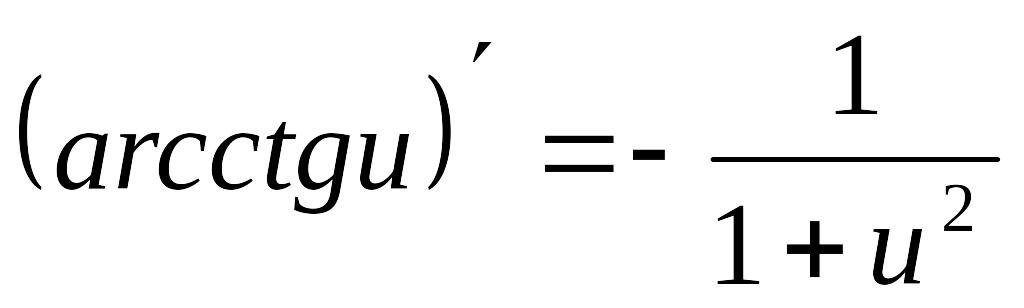
Мысалы,
формуласын
дәлелдейік.y=lnx
функциясының өсімшесі
![]() шаманы
шаманы
![]() -ке
бөліп туынды анықтамасын қолданайық:
-ке
бөліп туынды анықтамасын қолданайық:
![]() ,
,
мұнда екінші тамаша шектің салдарын қолдандық. Формуланы анықтама бойынша дәлелдедік.
Кері функцияның туындысы
y=f(x)
функциясына
кері функция (x=f
-
1(y))
туындысы:
![]() .
.
11.
Функцияның дифференциалы және жуықтап
есептеуге қолдану. Мысалдар. Функцияның
дифференциалы.
функциясының
шектелген туындысы бар болсын, онда:
![]() ,
демек
,
демек
![]()
![]() шексіз
аз шама.
шексіз
аз шама.
Онда
функцияның өсімшесі былай жазылады:
![]() .
Осы теңдікте екінші қосылғыш
.
Осы теңдікте екінші қосылғыш
![]() ,
,
![]() ке
қарағанда жоғарғы ретті шексіз аз шама
болғандықтан, бірінші қосылғыш
ке
қарағанда жоғарғы ретті шексіз аз шама
болғандықтан, бірінші қосылғыш
![]() ке
эквивалентті шама болады.
ке
эквивалентті шама болады.
Анықтама.Функцияның
туындысының аргументтің өсімшесіне
көбейтіндісін дифференциал деп атайды
және мына түрде жазады:
![]() .
Дербес жағдайда, егер
.
Дербес жағдайда, егер
![]() болса, онда
болса, онда
![]() ,
осыдан
,
осыдан
![]() және осыны пайдаланып дифференциалдың
формуласын былай жазуға болады:
және осыны пайдаланып дифференциалдың
формуласын былай жазуға болады:
![]() .
Осыдан
.
Осыдан
![]() ,
яғни туынды функцияның дифференциалының
аргумент дифференциалына бөлінген
мәніне тең.
,
яғни туынды функцияның дифференциалының
аргумент дифференциалына бөлінген
мәніне тең.
Дифференциалды
есептеу ережесі. Айталық
![]() және
және
![]() дифференциалданатын функциялар болсын,
дифференциалданатын функциялар болсын,
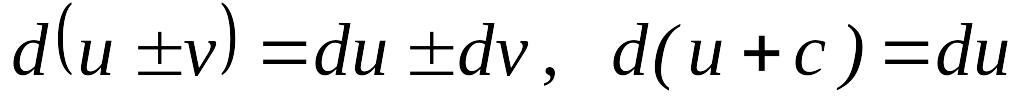 ,
мұндағыс
–сан.
,
мұндағыс
–сан.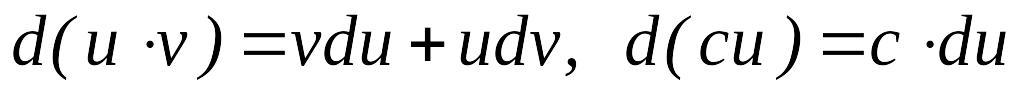 ,
,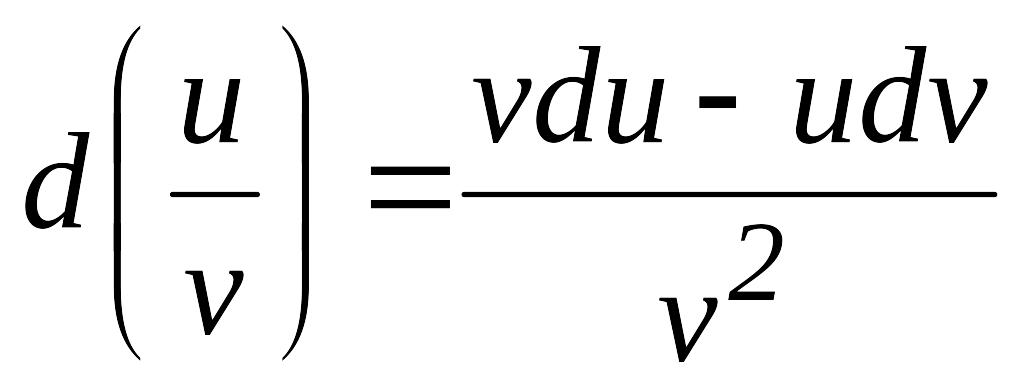 ,
егер
,
егер .
.Егер
 функциясы
функциясы нүктесінде дифференциалданатын,
ал
нүктесінде дифференциалданатын,
ал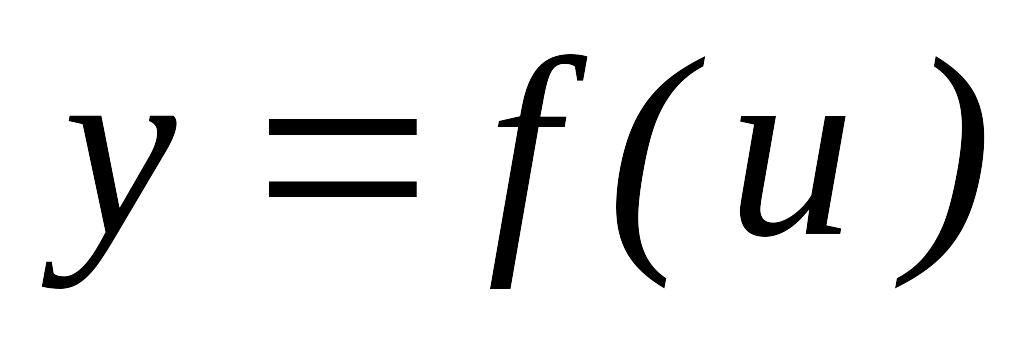
 нүктесінде дифференциалданатын болса,
онда
нүктесінде дифференциалданатын болса,
онда күрделі
функция үшін,
күрделі
функция үшін,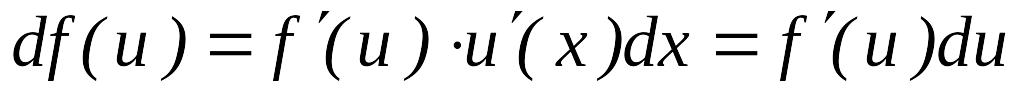 .
Бұл ережені бірінші
дифференциал формасының инварианттығы
деп атайды. Дифференциалды жуықтап
есептеуге қолдануға болады. Айталық,
функциясы
дифференциалданатын болсын, онда оның
өсімшесі:
.
Бұл ережені бірінші
дифференциал формасының инварианттығы
деп атайды. Дифференциалды жуықтап
есептеуге қолдануға болады. Айталық,
функциясы
дифференциалданатын болсын, онда оның
өсімшесі:
![]() ,
осыдан
,
осыдан
![]() .
.
Егер
![]() нүктесінде функцияның мәні берілсе,
онда:
нүктесінде функцияның мәні берілсе,
онда:
![]() .
.
мысал.![]() -ты
жуықтап есепте.
-ты
жуықтап есепте.
![]()
![]() .
.
12.
Лопиталь ережесі арқылы анықталмағандықты
ашу.Теорема
(Лопиталь ережесі).
f(x) және g(x) функциялары
![]() (
)
жағдайда нолге немесе шексіздікке
ұмтылсын. Егер олардың туындыларының
қатынасының шегі (ақырлы не ақырсыз)
бар болса, функциялар қатынасының да
шегі бар болады және мына қатынас
орындалады:
(
)
жағдайда нолге немесе шексіздікке
ұмтылсын. Егер олардың туындыларының
қатынасының шегі (ақырлы не ақырсыз)
бар болса, функциялар қатынасының да
шегі бар болады және мына қатынас
орындалады:![]() .
Лопиталь
ережесін қолданып ектерді есмептейік.
.
Лопиталь
ережесін қолданып ектерді есмептейік.
1.
![]() .
.
2.
3.
 .
.
Үшінші
мысалда Лопиталь ережесін бірден
қолдануға келмейді. Сондықтан, алгебралық
түрлендіру көмегімен
![]() түріндегі анықталмағандықты
түріндегі анықталмағандықты
![]() немесе
немесе
![]() түріндегі анықталмағандықтарға
келтіреміз. Осы мақсатпен х2
бөлімнің бөліміне түсірілді.
түріндегі анықталмағандықтарға
келтіреміз. Осы мақсатпен х2
бөлімнің бөліміне түсірілді.
4.
![]() .
Айталық
.
Айталық
![]() деп
белгілеп, теңдеудің екі жағын логарифмдейік.
Теңдеудіңоңжағынесептейік:
деп
белгілеп, теңдеудің екі жағын логарифмдейік.
Теңдеудіңоңжағынесептейік:
