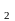Ограничимся доказательством теоремы для простейшего случая эргодического источника без памяти. Оно непосредственно вытекает из закона больших чисел, в соответствии с которым в длинной последовательности из N элементов алфавита l ( ), имеющих вероятности появления , содержится Np элементов , Np элементов и т. д.

Тогда вероятность ρ реализации любой типичной последовательности близка к величине

Логарифмируя правую и левую части выражения (4.6), получаем

откуда (при очень больших Ν)

Для общего случая теорема доказывается с привлечением цепей Маркова.

Покажем теперь, что за исключением случая равновероятного и независимого выбора букв источником, когда нетипичные последовательности отсутствуют, типичные последовательности при достаточно большом N составляют незначительную долю от общего числа возможных последовательностей.

При объеме алфавита источника l и количестве знаков в последовательности N число всех возможных последовательностей

Принимая во внимание соотношение (4.5), число типичных последовательностей n можно записать в виде

Тогда

Так как

то

и неравенство усиливается с увеличением N.

К. Шеннон показал, что рассмотренные свойства длинных последовательностей могут служить основанием для осуществления эффективного кодирования информации (см. § 5.4).

Пример 4.2. Оценить, какую долю общего числа возможных последовательностей следует учитывать в практических расчетах, если эргодический источник характеризуется параметрами l = 16, Η(Ζ) = 3,5 дв.ед , а N = 50.

В соответствии с (4.7) и (4.8) имеем

откуда

Следовательно, к типичным последовательностям относится только одна тридцатимиллионная доля всех возможных реализаций!

Избыточность. Следствием ограничений на выбор источником знаков является также недоиспользование их как переносчиков информации. Известная априорная информация о вероятностях выбора отдельных знаков и их сочетаний приводит к уменьшению средней неопределенности выбора источником знака, а следовательно, и переносимого им количества информации. При равновероятном и некоррелированном выборе ту же информационную нагрузку на знак можно обеспечить, используя алфавит меньшего объема. В связи с этим говорят об избыточности алфавита l источника сообщений или просто об избыточности источника.

Мерой избыточности служит величина D, показывающая, насколько хорошо используются знаки данного источника:

где (Z) — максимально возможная энтропия, равная log l; H(Ζ) — энтропия источника.

Если избыточность источника равна нулю, то формируемые им сообщения оптимальны в смысле наибольшего количества переносимой информации. Для передачи определенного количества информации I при отсутствии помех в этом случае необходимо k =I/[ (Z)] знаков.

Поскольку энтропия сообщений, формируемых реальным источником, обладающим избыточностью, меньше максимальной, то для передачи того же количества информации I знаков требуется больше, а именно: = I/H(Z) > k . Поэтому говорят также об избыточности знаков в сообщении или просто об избыточности сообщения, характеризуя ее тем же параметром D:

Избыточность нельзя рассматривать как признак несовершенства источника сообщений. Обычно она является следствием его физических свойств. Ограничения, существующие в любом естественном языке, связаны, например, с особенностями артикуляции, не позволяющими формировать слова, состоящие из произвольных сочетаний букв.

Последствия от наличия избыточности сообщений неоднозначны. С одной стороны, избыточные сообщения требуют дополнительных затрат на передачу, например, увеличения длительности передач или расширения практической ширины спектра канала связи, что нежелательно. С другой стороны, при использовании сообщений, подчиняющихся априорно известным ограничениям, появляется возможность обнаружения и исправления ошибок, которые приводят к нарушению этих ограничений. Следовательно, наличие избыточности способствует повышению помехоустойчивости сообщений. Высокая избыточность большинства естественных языков обеспечивает, например, надежное общение людей даже при наличии у них акцентов и дефектов речи.

Однако при обмене информацией в автоматических системах естественная избыточность подлежит устранению. Это объясняется тем, что алгоритмы обнаружения и исправления ошибок, базирующихся на статистических закономерностях функционирования источника, оказываются слишком сложными для реализации их техническими средствами. В случае необходимости для повышения помехоустойчивости затем вводится «рациональная» избыточность, позволяющая обеспечить обнаружение и исправление наиболее вероятных и опасных по последствиям ошибок простыми техническими средствами. При низком уровне помех в канале связи устранение избыточности приводит к увеличению скорости передачи информации и может дать значительный экономический эффект.

Пример 4.3. Определить возможный эффект от устранения избыточности при передаче текста на русском языке.

Максимальная энтропия текста на русском языке (с учетом пренебрежения при передаче различиями в буквах е и ё, ъ и ь) установлена ранее (см. пример 3.3) и равна 5 дв. ед. Там же определена энтропия с учетом неравномерного распределения вероятностей появления отдельных букв (4,42 дв. ед.). Имея сведения о переходных вероятностях и исходя из предположения, что текст представляет собой простую цепь Маркова, можно установить, что энтропия уменьшается до 3,52 дв. ед. Учет всех ограничений в языке, включая связи между словами, позволяет оценить минимальную величину энтропии значением 1,5 дв. ед. Таким образом, избыточность русского языка составляет

Это означает, что каналы связи, построенные без учета ограничений, существующих в языке, и способные передавать равновероятные буквы, следующие друг за другом в любых сочетаниях, при передаче информации без помех текстом на русском языке используется всего на 30 %. Полное устранение избыточности позволило бы повысить эффективность их использования более чем в 3 раза!

Производительность источника дискретных сообщений. Под производительностью источника сообщений подразумевают количество информации, вырабатываемое источником в единицу времени Эту характеристику источника называют также скоростью создания сообщений или потоком входной информации. Поскольку возможное воздействие помех на источник сообщений принято учитывать эквивалентным изменением характеристик модели канала связи, то производительность источника сообщений равна энтропии источника, приходящейся на единицу времени.

Длительность выдачи знаков источником в каждом из состояний в общем случае может быть различной. Обозначим длительность выдачи знака , формируемого источником в состоянии S , через τ . Тогда средняя длительность выдачи источником одного знака

Производительность источника Ī(z) теперь можно выразить формулой

Как следует из (4.10), повышение производительности источника возможно не только за счет увеличения энтропии, но и за счет снижения средней длительности формирования знака. Длительность знаков желательно выбирать обратно пропорциональными вероятностям их появления.

Если длительность выдачи знака не зависит от состояния источника, для всех знаков одинакова и равна τ, то τ = τ. Выражение для Ī(Z) принимает вид

Наибольшая производительность источника в этом случае достигается при максимальной энтропии.

Контрольные вопросы:

1. Модели источника дискретных сообщений

2. Свойства эргодических последовательностей знаков

3. Производительность источника дискретных сообщений

Тема 9. (Информационные характеристики источника непрерывных сообщений и непрерывных каналов связи.)

Цель лекции:

1. Изучить информационные характеристики источника непрерывных сообщений.

2. Информационные характеристики непрерывных каналов связи

Вопросы:

1. Понятие эпсилон.

2. Каковы информационные характеристики источника непрерывных сообщений?

3. Какие бывают информационные характеристики непрерывных каналов связи?

1. Информационные характеристики источника непрерывных сообщений

Эпсилон - производительность непрерывного источника сообщений. Под конкретным непрерывным сообщением 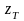(t) подразумевают некоторую реализацию случайного процесса длительностью Т. Источник непрерывных сообщений характеризуется ансамблем его реализаций. Наиболее плодотворной оказалась модель непрерывного сообщения в виде эргодического случайного процесса.

Для определения производительности источника непрерывных сообщений воспользуемся подходом и результатами § 3.7, где определена ε-энтропия случайной величины.

Под ε-производительностью источника непрерывных сообщений Ηε(z) понимают минимальное количество информации, которое необходимо создать источнику в единицу времени, чтобы любую реализацию (t) можно было воспроизвести с заданной вероятностью ε.

Допустим, что (t) воспроизводится реализацией uT(t). Наблюдаемые реализации следует рассматривать, как сигналы, обладающие ограниченным, хотя возможно и достаточно широким спектром F [28, 8].

При достаточно большой длительности Т как (t), так и uT(t) могут быть представлены N-мерными (N = 2FT) векторами ( ) и ( ), координатами которых являются отсчеты. Ансамбли сообщений { (t)} и воспроизводящих сигналов {uT(t)} характеризуют при этом N-мерными случайными векторами Ζ и U, составляющими которых являются соответственно случайные величины Ζ1, Z2, .., ZN и U1, U2, .., UN. Статистическое описание каждого из ансамблей задается N-мерными плотностями распределения вероятностей ρ(Ζ) = ρ( ) и p(U) = p( ). Связь между ансамблями отражают условные плотности распределений pu(Z)= = ρ( / ) и pz(U) = p( / ), а также совместная плотность распределения вероятностей p(Z,U) = p( ; ).

Распространяя формулу (4.20) на N-мерные случайные векторы Ζ и U для количества информации одного из них относительно второго, получим

где интегралы являются N-мерными.

Используем, как и ранее, среднеквадратический критерий верности (Z,U), который в рассматриваемом случае имеет вид

где p(Z,U)ZU представляет собой квадрат расстояния l(Z,U) в N-мерном евклидовом пространстве.

Количество информации, приходящееся в среднем на один отсчет дискретизованных сигналов ZT(t) и UT(t), определяется выражением

Тогда в соответствии с определением для ε-пропорциональности источника непрерывных сообщений Нε(Z) запишем

при выполнении условия

Величина ν характеризует скорость формирования источником отсчетов (ν = =2F).

Пример 4.5. Определить ε-производительность источника, формирующего со скоростью ν1 некоррелированные отсчеты стационарного нормального случайного сигнала с дисперсией σ2.

Воспользовавшись полученным в (3.65) значением ε-энтропии для нормально распределенной случайной величины, найдем

Возможности воспроизведения любого сообщения zT(t) с заданной верностью можно дать геометрическое толкование. Поскольку все реализации эргодического процесса достаточно большой длительности являются типичными и обладают практически одной и той же средней мощностью, концы соответствующих им векторов в N-мерном пространстве сообщений составляют непрерывное множество точек, равноудаленных от начала координат (гиперсферу).

Конечное подмножество воспроизводящих сигналов UT(t) размещается в центрах непересекающихся правильных сферических N-угольников (ε-областей), на которое гиперсфера разбивается без промежутков. Размеры ε-областей определены заданной верностью воспроизведения сообщений. Если источником реализуется сообщение z*T(t), конец вектора которого должен попасть в ε-область сигнала u*T(t), то воспроизводится сигнал u*T(t).

Следует отметить, что заданная верность воспроизведения будет достигнута с вероятностью, близкой к единице, только при достаточно большой длительности сообщений, когда погрешностью от замены непрерывных реализаций последовательностями отсчетов можно будет пренебречь. Для уменьшения указанной погрешности при ограниченной длительности сообщений Т необходимо увеличивать число отсчетов N. В пределе при N→∞ получим непрерывные реализации.

В вычислении ε - производительности источника и геометрическом толковании возможности воспроизведения сообщений с заданной верностью принципиально ничего не изменяется. Следует лишь учесть, что N-мерное евклидово пространство сообщений становится гильбертовым и мерой близости двух сигналов должно быть расстояние в этом пространстве.