2. Транспортная несбалансированная задача с дефицитом

Пусть на складе П3 хранится не 2500 штук продукции (как в предыдущем примере), а 2100 штук. Остальные условия предыдущей задачи оставляем без изменения. Таким образом, предложение (6100 штук) меньше спроса (6500 штук)  имеем дефицит предложения. Поэтому такая задача называется задачей с дефицитом. Ограничения для таких задач для пунктов отправления записываются в виде равенств, а для пунктов назначения  в виде неравенств. Ограничения для складов компании имеют вид

Х₁₁ + Х₁₂ + Х₁₃ + Х₁₄ = 1000

Х₂₁ + Х₂₂ + Х₂₃ + Х₂₄ = 3000

Х₃₁ + Х₃₂ + Х₃₃ + Х₃₄ = 2100

Записываем ограничения для складов покупателей

Х₁₁ + Х₂₁ + Х₃₁ ≤ 1300

Х₁₂ + Х₂₂ + Х₃₂ ≤ 800

Х₁₃ + Х₂₃ + Х₃₃ ≤ 2700

Х₁₄ + Х₂₄ + Х₃₄ ≤ 1700

Табличная модель для этой математической модели полностью повторяет табличную модель для сбалансированной задачи (рис. 1) за исключением того, что в ячейке G14 вместо 2500 введено 2100, а в ячейках В16 : Е16 вместо знака «=» стоит знак «≤». Изменения коснутся только установок диалогового окна Поиск решения, где ограничения $B$15 : $Е$15 = $B$16 : $E$16 (рис. 3) заменяются ограничениями $B$15 : $Е$15 ≤ $B$16 : $E$16. Найденное решение показано на рис. 4.

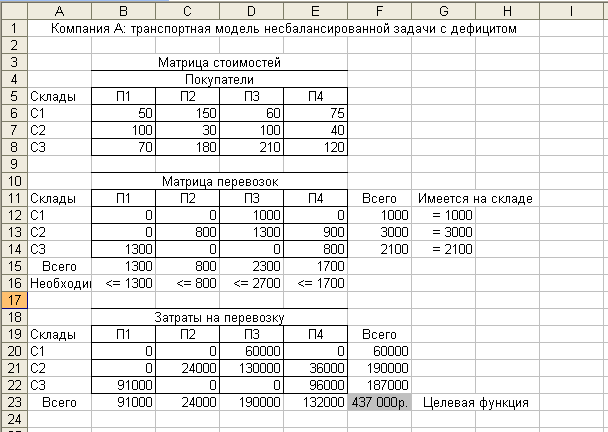
Рис. 4

Полученное решение почти в точности повторяет решение сбалансированной задачи за исключением того, что теперь покупатель П3 недополучит 400 штук продукции. Общая стоимость всех перевозок составит 437 тыс. руб. (значение целевой функции в ячейке F23).

3. Транспортная несбалансированная задача с избытком

Пусть на складе П3 хранится не 2500 штук продукции (как в примере сбалансированной задачи), а 2900 штук. Остальные условия сбалансированной задачи оставляем без изменения. Таким образом, предложение (6900 штук) больше спроса (6500 штук)  имеем избыток предложения. Поэтому такая задача называется задачей с избытком. Ограничения для таких задач для пунктов отправления записываются в виде неравенств, а для пунктов назначения  в виде равенств. Ограничения для складов компании имеют вид

Х₁₁ + Х₁₂ + Х₁₃ + Х₁₄ ≤ 1000

Х₂₁ + Х₂₂ + Х₂₃ + Х₂₄ ≤ 3000

Х₃₁ + Х₃₂ + Х₃₃ + Х₃₄ ≤ 2900

Записываем ограничения для складов покупателей:

Х₁₁ + Х₂₁ + Х₃₁ = 1300

Х₁₂ + Х₂₂ + Х₃₂ = 800

Х₁₃ + Х₂₃ + Х₃₃ = 2700

Х₁₄ + Х₂₄ + Х₃₄ = 1700

Табличная модель для этой математической модели полностью повторяет табличную модель для сбалансированной задачи (рис. 1) за исключением того, что в ячейке G14 вместо 2500 введено 2900, а в ячейках G12 : G14 вместо знака «=» стоит знак «≤». Изменения коснутся установок диалогового окна Поиск решения, где ограничения $F$12 : $F$14 = $G$12 : $G$14 (рис. 3) заменяются ограничениями $F$12 : $F$14 ≤ $G$12 : $G$14. Найденное решение показано на рис. 5.

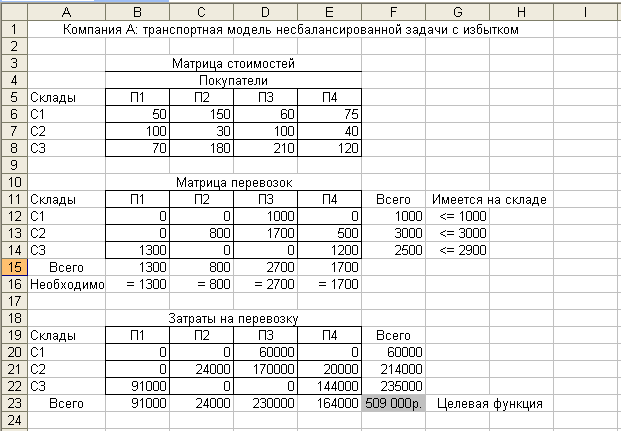
Рис. 5

Полученное решение почти в точности повторяет решение сбалансированной задачи за исключением того, что теперь со склада С3 вывозится не вся продукция  400 шт. остается. Общая стоимость всех перевозок составит 509 тыс. руб. (значение целевой функции в ячейке F23), как и в сбалансированной задаче.

4. Задача о назначениях математической модели линейного программирования

Задача о назначениях является частным случаем транспортной задачи, имеет такую же структуру, но обладает и своими особенностями. В простейшем случае задача о назначениях формулируется следующим образом. Имеется n различных работ и столько же работников, претендующих на выполнение этих работ. На выполнение каждого вида работ назначается только один работник, при этом каждый работник может выполнить любую работу, но за свою плату и в свое время. Необходимо так распределить работы между работниками, чтобы минимизировать суммарные денежные затраты или суммарное время выполнения всех работ.

Если количества работников и работ равны, то такая задача о назначениях называется сбалансированной, в противном случае задача будет несбалансированной.

Сбалансированной будет также задача, если на некоторые процессы требуется несколько работников, но при этом общие количества требуемых и имеющихся работников совпадает. Такая задача называется задачей о назначениях для коллективной работы.

Линейная целевая функция n переменных имеет вид

Z = c₁₁ x₁₁ + c₁₂ x₁₂ +……+c_nn x_nn

Эту целевую функцию следует минимизировать, если коэффициенты c_ij выражают стоимости назначения работника i на выполнение работы j. Эта стоимость может выражаться в денежном эквиваленте, длительности времени выполнения работы или может быть каким - либо другим показателем эффективности назначения именно этого работника на данный процесс. Переменные x_ij  это переменные будущего решения задачи. Они определяются так: x_ij = 1, если работник i назначается на выполнение работы j, и x_ij = 0, если работник i не назначается на выполнение работы j. Эти переменные являются двоичными переменными. Они могут принимать только одно из двух значений  0 или 1.

Рассмотрим ограничения для сбалансированной задачи (без условия коллективной работы). Имеем n ограничений в виде равенств для каждого работника (суммы по строкам):

x₁₁ + x₁₂ +……+ x_1n = 1

x₂₁ + x₂₂ +……+ x_2n = 1

…… …… ……

x_n1 + x_n2 +……+ x_nn = 1

Аналогично имеем n ограничений в виде равенств для каждой работы (суммы по столбцам).

x₁₁ + x₂₁ +……+ x_n1 = 1

x₁₂ + x₂₂ +……+ x_n2 = 1

…… …… ……

x_1n + x_2n +……+ x_nn = 1