1. Транспортная сбалансированная задача

Для иллюстрации решения задачи 6 рассмотрим следующий пример: Компания А хранит свою готовую продукцию на трех складах: С1, С2 и С3, расположенных в разных частях города. На этих складах хранится продукция в количестве 1000, 3000 и 2500 штук соответственно. Продукцию необходимо доставить четырем оптовым покупателям: П1, П2, П3 и П4, заявки которых составляют 1300, 800, 2700 и 1700 штук соответственно.

Переменные решения Х₁₁, Х₁₂, …….. Х₃₄ обозначают количество продукции, перевозимой со складов компании на соответствующие склады покупателей. Например, переменная Х₂₁ обозначает количество продукции, перевозимой со склада С2 на склад покупателя П1. Стоимости (в рублях) доставки одной штуки продукции со складов компании на склады покупателей показаны в табл. 7.

Таблица 2

Склады компании	Оптовые покупатели
	П1	П2	П3	П4
С1	50	150	60	75
С2	100	30	100	40
С3	70	180	210	120

В соответствии с введенными переменными целевая функция запишется так:

Z = 50 Х₁₁ + 150 Х₁₂ + 60 Х₁₃ + 75 Х₁₄ + 100 Х₂₁ + 30 Х₂₂ + 100 Х₂₃ + 40 Х₂₄ + 70 Х₃₁ + 180 Х₃₂ + 210 Х₃₃ + 120 Х₃₄

Данную целевую функцию следует минимизировать, т.е. определить самую минимальную стоимость транспортировки продукции.

Ограничения для складов компании имеют вид

Х₁₁ + Х₁₂ + Х₁₃ + Х₁₄ = 1000

Х₂₁ + Х₂₂ + Х₂₃ + Х₂₄ = 3000

Х₃₁ + Х₃₂ + Х₃₃ + Х₃₄ = 2500

Ограничения для складов покупателей имеют вид

Х₁₁ + Х₂₁ + Х₃₁ = 1300

Х₁₂ + Х₂₂ + Х₃₂ = 800

Х₁₃ + Х₂₃ + Х₃₃ = 2700

Х₁₄ + Х₂₄ + Х₃₄ = 1700

Теперь перенесем математическую модель в табличную модель MS Excel, показанную на рис.1.

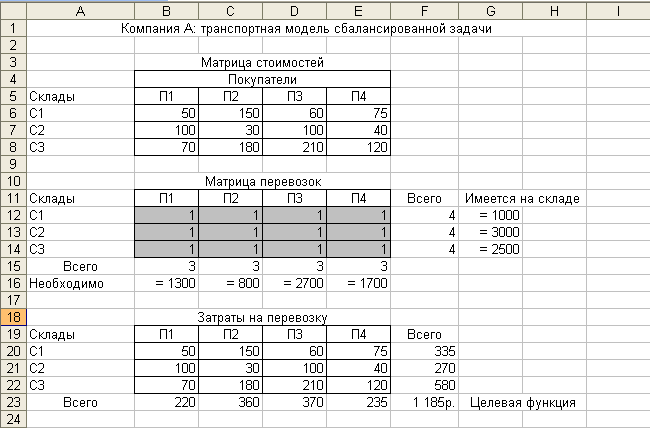
Рис. 1

Пояснения к рис. 1

В табличной модели отображены две матрицы  стоимостей и перевозок (решений). Матрица стоимостей располагается в диапазоне В6:Е8, а матрица перевозок  в диапазоне В12:Е14. Матрица перевозок содержит переменные решения, они выделены серым цветом. На рис. 1 все переменные пока равны 1.

Матрицу перевозок обрамляют столбец и строка с заголовками Всего, где подсчитываются суммы переменных соответственно по строкам и столбцам матрицы перевозок. Это значения левых частей ограничений. Правые части ограничений содержатся в столбце Имеется на складе (ограничения для складов компании) и в строке Необходимо (ограничения для складов покупателей).

Теперь можно приступать к поиску оптимального решения. Запускаем средство Поиск решения с помощью команды меню Сервис  Поиск решения. Если в пункте меню Сервис команды Поиск решения нет, то ее следует включить в этот пункт меню с помощью команды Сервис  Надстройки. В диалоговом окне Поиск решения задаем адрес целевой ячейки F23, устанавливаем переключатель минимальному значению, указываем адрес диапазона изменяемых ячеек В12:Е14. После этого диалоговое окно должно выглядеть так, как показано на рис. 2.

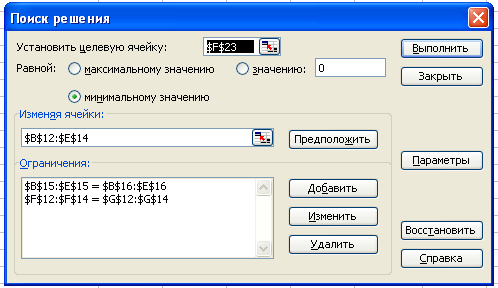
Рис. 2

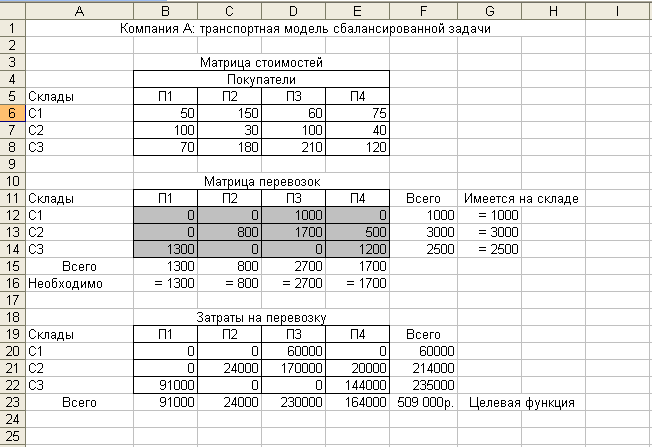
Рис. 3

В диалоговом окне Параметры поиска решения следует установить флажки Линейная модель, Неотрицательные значения и Автоматическое масштабирование. В диалоговом окне Поиск решения щелкаем по кнопке Выполнить и получаем решение, показанное на рис. 3.

В соответствии с полученным решением со склада С1 компании надо перевезти весь имеющийся там груз (в объеме 1000 штук) на склад покупателя (ячейка D12). При этом затраты на транспортировку составят 60 тыс. руб. (ячейка D20). Со склада С2 следует 800 1700 и 500 штук продукции отправить на склады покупателей П2, П3 и П4 соответственно (ячейки С13 : Е13), а затраты на перевозку составят 24, 170 и 20 тыс. руб. (ячейки С21 : Е21). Со склада С3 1300 штук продукции отправятся на склад покупателя П1 (ячейка В14) при затратах 91 тыс. руб. (ячейка В22) и 1200 штук отправятся на склад покупателя П4 (ячейка Е14) при затратах 144 тыс. руб. (ячейка Е22). Общая стоимость всех перевозок составит 509 тыс. руб. (значение целевой функции в ячейке F23).