1.9.2. Непрерывная случайная величина
Определение. Случайная величина Х называется непрерывной, если она может принимать любые значения из некоторого конечного интервала.
Например, суточный расход воды городом, скорость движущего тела, напряжение электрической сети и т. д.
Так как непрерывная случайная величина всегда принимает бесчисленное множество значений, то ее нельзя задать так же, как задается дискретная случайная величина.
Непрерывная случайная величина может быть задана непрерывной функцией распределения (интегральной функцией распределения вероятностей), а также плотностью вероятности (дифференциальной функцией распределения вероятностей).
Дискретная случайная величина может быть задана так же интегральной функцией распределения.
Определение. Интегральной функцией распределения F(x) случайной величины Х называется функция, которая для каждого значения х определяет вероятность того, что случайная величина Х примет значение меньшее х, то есть
F(х)=Р(Х<х).
Если случайная величина Х дискретная, то функция F(х) разрывная.
Вероятность того, что случайная величина примет значение, принадлежащее отрезку [a; b], равна приращению интегральной функции распределения, то есть
.
Определение. Плотностью вероятности f(х) или дифференциальной функцией распределения вероятностей называется первая производная от функции распределения:
f(х)=F'(х).
Функция распределения является первообразной для плотности вероятности.
Вероятность попадания случайной величины x в заданный интервал значений [а, b] вычисляется как определенный интеграл от плотности вероятностей:
.
Определение. Математическим ожиданием М(Х) непрерывной случайной величины X, все возможные значения которой принадлежат отрезку [а, b], называется определенный интеграл от произведения хf(х), взятый в пределах от а до b, то есть
.
Если непрерывная случайная величина Х принимает значения, принадлежащие всей числовой оси, то ее математическое ожидание равно:
.
Определение. Дисперсия непрерывной случайной величины Х, все значения которой принадлежат отрезку [а, b] вычисляется по формуле:
.
Если же случайная величина Х принимает значения, принадлежащие всей числовой оси, то
.
Определение.
Среднее
квадратическое отклонение
непрерывной случайной величины Х
равно
.
1.10. Законы распределения случайных величин
1.10.1. Биномиальный закон распределения
Рассмотрим n повторных независимых испытаний. В результате каждого испытания может наступить некоторое событие А, причем вероятность наступления события А в каждом отдельном испытании не зависит от результатов предшествующих и последующих испытаний и равна р.
Для нахождения вероятности того, что в серии из n испытаний событие А появится ровно k раз, воспользуемся формулой Бернулли (1.20.1):
.
Рассмотрим случайную величину Х, представляющую собой число появления событий и соответствующие вероятности:
Х |
0 |
1 |
2 |
… |
k |
… |
n |
р |
qn |
|
|
… |
|
… |
pn |
Как видно, вероятность того, что в n независимых испытаниях случайная величина Х примет значения k, определяется по формуле Бернулли (1.20) или (1.20.1). В этом случае говорят, что случайная величина Х распределена по биномиальному закону распределения. Такое название она получила за то, что правая часть формулы в точности представляет собой члены суммы разложения бинома (p+q)n.
.
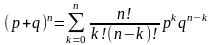Числа p и q в биномиальном законе распределения определяются условиями эксперимента, а число испытаний n устанавливается заранее. Вероятность появления данного события k раз в серии из n испытаний является функцией числа k. То есть число появления события k, является случайной величиной.
Математическое ожидание биномиального закона распределения равно M(X)= np.
Дисперсия
и среднеквадратическое отклонение
биномиального закона распределения
равны:
.
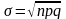Пример 1.10. Составить закон распределения выпадения герба при двух подбрасываниях монеты.
Решение.
При n=2 подбрасываниях монеты герб может выпасть k=0;1;2 раза. Подбрасывание монеты два раза – это повторные независимые испытания. Вероятность выпадения герба при одном подбрасывании монеты величина постоянная и равная р=½.
Определим вероятность появления герба k раз по формуле Бернулли (1.20).
Вероятность того, что из двух подбрасывания монеты герб ни разу не выпадет:
.
Вероятность того, что из двух подбрасывания монеты герб выпадет один раз:
.
Вероятность того, что из двух подбрасывания монеты герб выпадет два раза:
.
Сумма вероятностей: Р2(0) + Р2(1) + Р2(2) = 1.
Биноминальный закон распределения имеет вид:
Х |
0 |
1 |
2 |
р |
0,25 |
0,5 |
0,25 |