11. Застосування теорії ігор у виборі рішень.

11.1. Суть теорії ігор і її завдання.

Досить часто рішення приходиться приймати в умовах невизначеності, тобто в таких умовах, коли процес виконання операції невизначений, чи нам свідомо протидіє супротивник, чи немає ясних і чітких цілей (завдань) операції. Наслідком невизначеності є те, що успіх операції залежить не тільки від наших рішень, але й від чиїхось рішень чи дій.

В цілій низці завдань приходиться аналізувати ситуації, в яких зіштовхуються якісь протиборствуючі сторони (дві або більше), кожна з яких переслідує свою мету, причому результат будь-якого міроприємства кожної з сторін залежить від того, яких заходів вживе супротивник. Такі ситуації називають конфліктними, вивченням яких і займається теорія ігор.

Теорію ігор можна визначити як теорію математичних моделей прийняття рішень в умовах конфлікту.

Серед завдань, що вимагають застосування теорії ігор, можна назвати наступні:

• аналіз конфліктних ситуацій у військових і економічних галузях (простим економічним прикладом конфліктної ситуації, для опису якої використовується теорія ігор, є конкурентна боротьба торгових фірм чи промислових підприємств);

• обмінні і торгові операції;

• взаємовідносини між постачальником і споживачем;

• взаємовідносини між покупцем і продавцем;

• взаємовідносини між банком і клієнтом;

• аналіз і проектування ієрархічних структур управління і економічних механізмів (наприклад, аналіз різних моде лей стимулювання);

• аналіз доцільності права першого ходу, взаємної інформованості, можливості блефувати;

• аналіз коаліційної поведінки;

• ряд інших завдань.

В наведених прикладах в їх основі лежить конфліктна ситуація, яка породжується відмінністю інтересів супротивників чи партнерів і прагненням кожного з них досягти переваг, досягаючи оптимального рішення. Кожному учаснику такого суперництва приходиться рахуватися не тільки з власними цілями, але й з інтересами партнера.

Мета гри — виграш одного з партнерів з врахуванням відповідних дій партнера (суперника чи супротивника).

Теорія ігор розрахована для рішень в іграх, в які грають тільки один раз. Якщо гра повторюється, то треба використати статистичні методи. В одиничній, неповторній грі теорія ігор або дозволяє вибирати одне визначене рішення «найкраще» з багатьох можливих рішень, або одержати характеристики того випадкового механізму, з допомогою якого один раз вибирається якесь одне з можливих рішень.

На змістовному рівні під грою можна розуміти взаємодію декількох осіб (гравців), що має кінцевий стан (виграш), якого прагне кожен гравець, але не кожен може досягти. Прикладом гри може бути боротьба декількох фірм за державне замовлення [33]. Система умов, що регламентує можливі варіанти дій сторін, об'єм інформації кожної сторони про поведінку іншої, а також результат, до якого приводить дана сукупність дій, складають правила гри.

Кожен гравець має багато можливих ходів. Вибрати один з них — зробити хід. Послідовність ходів, що приводять гру до кінцевого стану, називається партією.

Сукупність правил, що визначають вибір варіанта дій під час кожного ходу в залежності від обстановки, що склалася, називається стратегією.

Результатом гри є виграш чи програш одної з сторін, як правило виражений в кількісній формі. Наприклад, математичне очікування доходу чи прибутку.

Оптимальною стратегією буде така, яка при багаторазовому повторенні гри забезпечує даній стороні максимально можливий середній виграш.

Ігри, в яких одна сторона програє стільки, скільки виграє інша, називаються іграми з нульовою сумою. Тут будуть розглядатися тільки парні ігри з нульовою сумою.

В загальному вигляді постановка завдання теорії ігор подається наступним чином. Нехай маємо деяку операцію (цілеспрямована дія), в якій приймають участь дві сторони А і В з протилежними інтересами:

• наявні правила гри, що регламентують результати, до яких приводять можливі варіанти дій сторін;

• результата дій сторін (виграші) виражені в кількісній формі і зазначені а (математичне очікування виграшу сторони А, що зробила свій і-й хід при j-му ході сторони В).

Умови гри звичайно записуються в формі платіжної матриці чи матриці гри (табл. 11.1).

Таблиця 11.1

Матриця гри

В1 А1	В1	В2		Вn
А1	а11	а12		а1n
А2	а21	а22		а2n
				
Аm	аm1	аm2		аmn

В даній грі сторона А (ми) має т стратегій, а сторона В (супротивник) — п стратегій (гра тхп).

Необхідно знайти найкращі (оптимальні) стратегії сторін, а також очікуваний середній виграш (результат).

При вирішенні гри зустрічаються наступні поняття:

= max і = max min іj — максимін чи нижня ціна гри;

= тіп і = min max ij — мінімакс чи верхня ціна гри.

Одержання максиміну і мінімаксу ясно з розгляду матриці гри (див. табл. 10.1).

В тих випадках, коли  =  гра має сідлову точку — елемент матриці, що є одночасно мінімальним в своєму рядку і максимальним в своєму стовпці.

Загальне значення нижньої і верхньої ціни гри  =  =  називається чистою ціною гри.

Сідловій точці відповідає пара стратегій сторін (стратегії А, і В), які є оптимальними. Сукупність цих стратегій називається вирішенням гри в чистих стратегіях.

У тих випадках, коли , рішення знаходиться в змішаних стратегіях. Змішаними стратегіями називаються такі, які одержують шляхом випадкового чергування чистих стратегій.

Змішана стратегія сторони А позначається

,

де - ймовірності, з якими застосовуються стратегії А₁, А₂,...А» причому .

Аналогічно для сторони В:

,

дe .

Вирішенням гри в змішаних стратегіях буде пара оптимальних змішаних стратегій, позначених S*_A і S*_B. Виграш, що відповідає цьому рішенню, називається ціною гри .

Стосовно до ігор 2x2 змішані стратегії набувають дещо іншого вигляду:

;

;

;

;

(11.1)

Стратегії, що входять в оптимальну стратегію з ймовірностями, відмінними від нуля, називаються активними.

. (11.2)

Гра 2x2 має наступне геометричне вирішення (рис. 11.1):

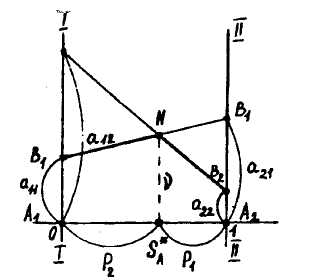
Рис. 11.1. Геометричне вирішення гри 2x2

• на відрізку осі абсцис, довжина якого дорівнює одиниці, лівий кінець (х = 0) означає стратегію А₁, а правий (х = 1) — стратегію А₂; проміжні точки участку відображають змішані стратегії сторони А;

• через точки А₁, і А₂ проводяться перпендикуляри до осі абсцис: осі 1-1 і II—II. На осі 1-1 відкладаються виграші при стратегії А₁, а на осі ІІ-ІІ — виграші при стра тегії А₂;

• стратегія супротивника B₁, дає на осях 1-1 і ІІ-ІІ точки з координатами а₁₁ і а₁₂ відповідно, а стратегія В₂ — точ ки з координатами а₁₂ і а₂₂ відповідно;

• ордината точки N перетину стратегій В₁, і В₂ дає величину виграшу н — ціну гри. Абсциса точки N дає ймовірності обох стратегій p₁ і р₂, які дорівнюють відстанням від точки S* до правого і лівого кінця відрізка А₁,А₂ відповідно.

Нижня (гарантована) межа виграшу виділена на рис. 11.1. жирною лінією.

На рис. 11.2 показана аналогічна побудова для гри 2x3.

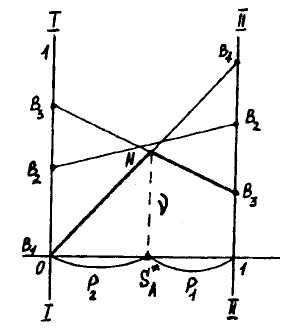
Рис. 11.2. Геометричне вирішення гри 2x3