
- •Содержание
- •1. Постановка задачи линейного программирования.
- •2. Существующие математические программные системы.
- •3. Решение задачи линейного программирования графическим методом.
- •4. Геометрическая интерпретация двойственных задач.
- •5. Симплексный метод.
- •6. Транспортная задача.
- •7. Задачи теории игр и линейное программирование.
- •8. Сведение задач теории игр к задачам линейного программирования.
- •Литература
8. Сведение задач теории игр к задачам линейного программирования.
Чтобы найти решение данной игры, определяемой матрицей А, нужно составить следующую пару двойственных задач и найти их решение [6].
Прямая задача: найти максимальное
значение функции
![]() при условиях
при условиях
![]()
![]() ,
,
![]() ,
,
![]() .
.
Двойственная задача: найти минимальное
значение функции
![]() при условиях
при условиях
![]() ,
,
,
,
![]() ,.
.
,.
.
Используя решение пары двойственных задач, получаем формулы для определения оптимальных стратегий и цены игры:
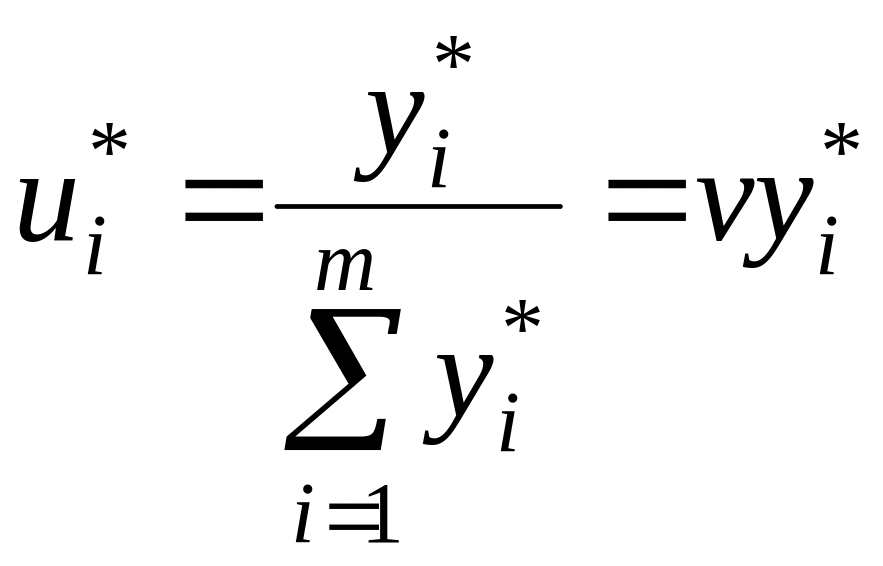 ,
,
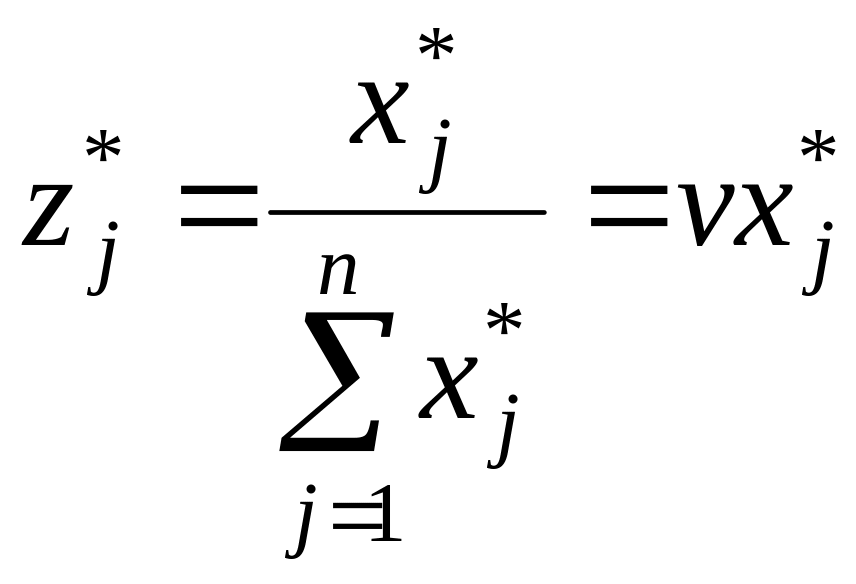 ,
,
 ,
,
.
,
,
.
Итак, процесс нахождения решения игры с использованием методов линейного программирования включает в себя следующие этапы:
Составляют пару двойственных задач линейного программирования, эквивалентных данной матричной игре.
Определяют оптимальные планы пары двойственных задач.
используя соотношения между планами пары двойственных задач и оптимальными стратегиями и ценой игры, находят решение игры.
Пример 7. Найти решение игры, заданной матрицей:
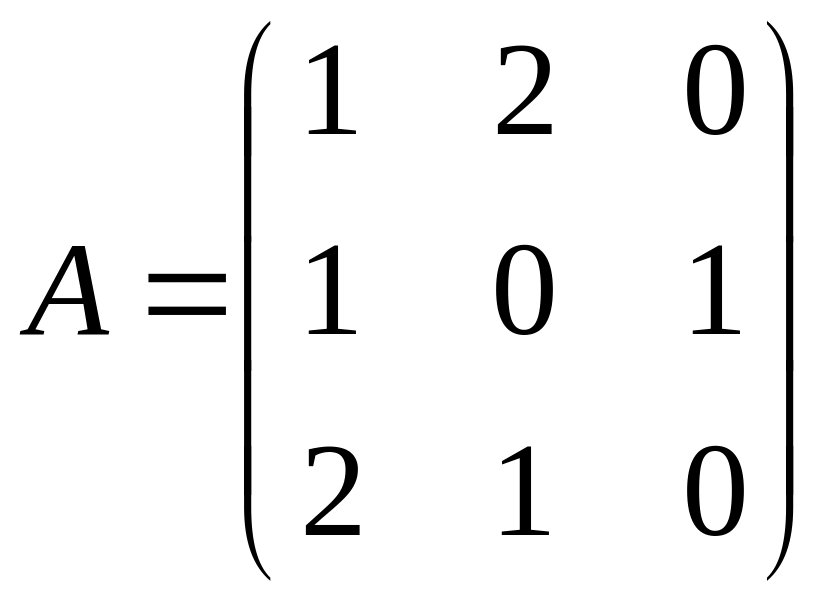 .
.
Решение. Составим двойственную пару
задач линейного программирования.
Прямая задача: найти максимум функции
![]() при ограничениях
при ограничениях
![]()
![]() .
.
Двойственная задача: найти минимум
функции
![]() при ограничениях
при ограничениях
![]()
![]() .
.
Находим оптимальные планы прямой и двойственной задач:
|
базис |
Сб |
Р0 |
1 |
1 |
1 |
0 |
0 |
0 |
Р1 |
Р2 |
Р3 |
Р4 |
Р5 |
Р6 |
||||
1 |
Р4 |
0 |
1 |
1 |
2 |
0 |
1 |
0 |
0 |
2 |
Р5 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
3 |
Р6 |
0 |
1 |
2 |
1 |
0 |
0 |
0 |
1 |
|
|
|
0 |
-1 |
-1 |
-1 |
0 |
0 |
0 |
1 |
Р4 |
0 |
1 |
1 |
2 |
0 |
1 |
0 |
0 |
2 |
Р3 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
3 |
Р6 |
0 |
1 |
2 |
1 |
0 |
0 |
0 |
1 |
|
|
|
1 |
0 |
-1 |
0 |
0 |
1 |
0 |
1 |
Р2 |
1 |
|
|
1 |
0 |
|
0 |
0 |
2 |
Р3 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
0 |
3 |
Р6 |
0 |
|
|
0 |
0 |
|
0 |
1 |
|
|
|
|
|
0 |
0 |
|
1 |
0 |
Из таблицы видно, что исходная задача
имеет оптимальный план
![]() ,
а двойственная задача- оптимальный план
,
а двойственная задача- оптимальный план
![]() .
Следовательно, цена игры
.
Следовательно, цена игры
 ,
а оптимальные стратегии игроков
,
а оптимальные стратегии игроков
![]() ,
,
![]() .
.
Задания.
Порядок выбора вариантов.
Всего в работе 4 задачи. Номера вариантов по каждому заданию выбираются по буквам фамилии студента в соответствии с таблицей:
№ варианта |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
буквы |
А |
Б |
В |
Г |
Д |
Е |
Ё |
Ж |
З |
И |
К |
Л |
М |
Н |
О |
П |
Р |
С |
Т |
У |
|
Ф |
Х |
Ц |
Ч |
Ш |
Щ |
Ъ |
Ы |
Ь |
Э |
|
Ю |
Я |
|
|
|
|
|
|
|
|
Если фамилия студента состоит меньше, чем из четырех букв, недостающие буквы берутся с начала фамилии. Например, для студента с фамилией Петров должны быть выбраны следующие варианты заданий:
Из первой задачи условие № 6 (буква П);
Из второй задачи условие № 6 (буква Е);
Из третьей задачи условие № 9 (буква Т);
Из четвертой задачи условие № 7 (буква Р).
Работа должна быть выполнена в тетради с приведением всех необходимых вычислений.
Задача 1. Решить задачи симплекс-методом, дать решению геометрическую интерпретацию. Во всех заданиях иметь в виду, что переменные неотрицательны.
1.
![]() 2.
2.
![]()
3.
![]() 4.
4.
![]()
5.
![]() 6.
6.
![]()
7.
![]() 8.
8.
![]()
9.
![]() 10.
10.
![]()
Задача 2. На трех складах А, В,
С находится горючее, соответственно
50, 90, 110 тонн, которое надо доставить в
три пункта: в пункт 1 – 70 т, в пункт 2 –
100 т, в пункт 3 – Х т. Стоимость доставки
одной тонны горючего со склада А в
указанные пункты соответственно равны
![]() ,
,
![]() ,
,
![]() грн., со склада В -
грн., со склада В -
![]() ,
,
![]() ,
,
![]() грн., со склада С -
грн., со склада С -
![]() ,
,
![]() ,
,
![]() грн.
грн.
Используя условия баланса транспортной задачи, найти потребности в горючем пункта 3, определить оптимальный план перевозки горючего в три пункта, минимизирующий стоимость перевозок.
1.
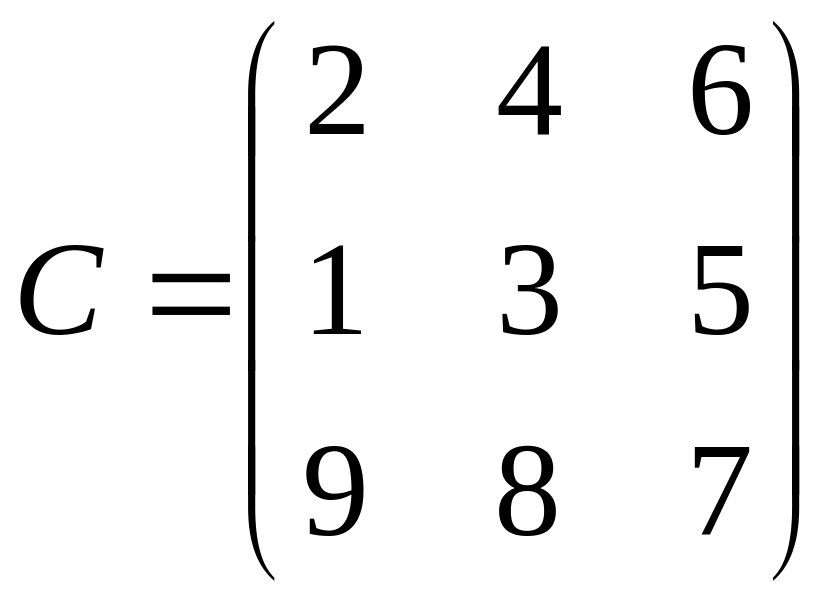 .
2.
.
2.
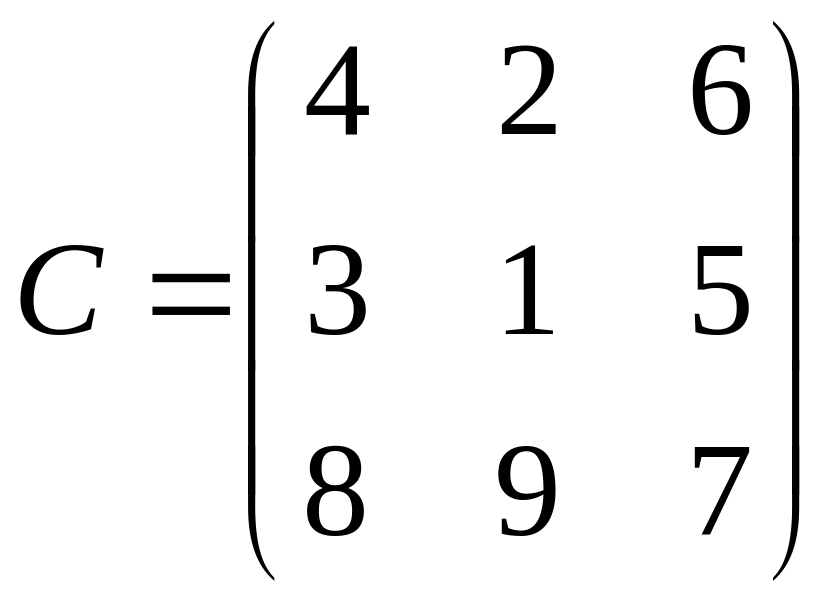 .
3.
.
3.
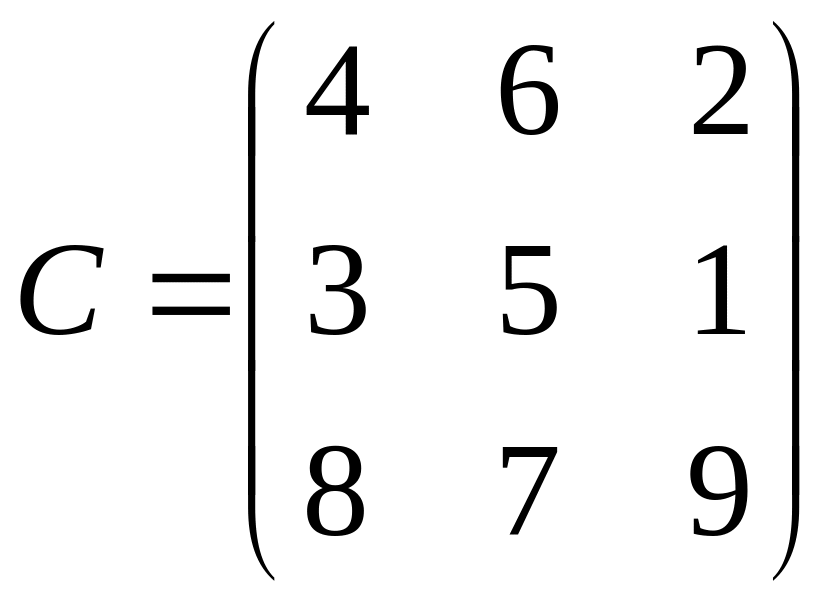 .
4.
.
4.
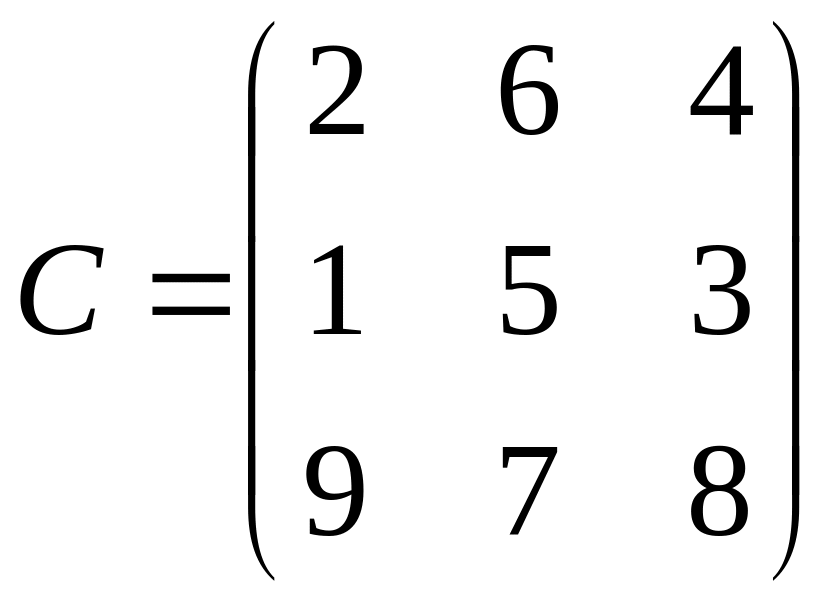
5.
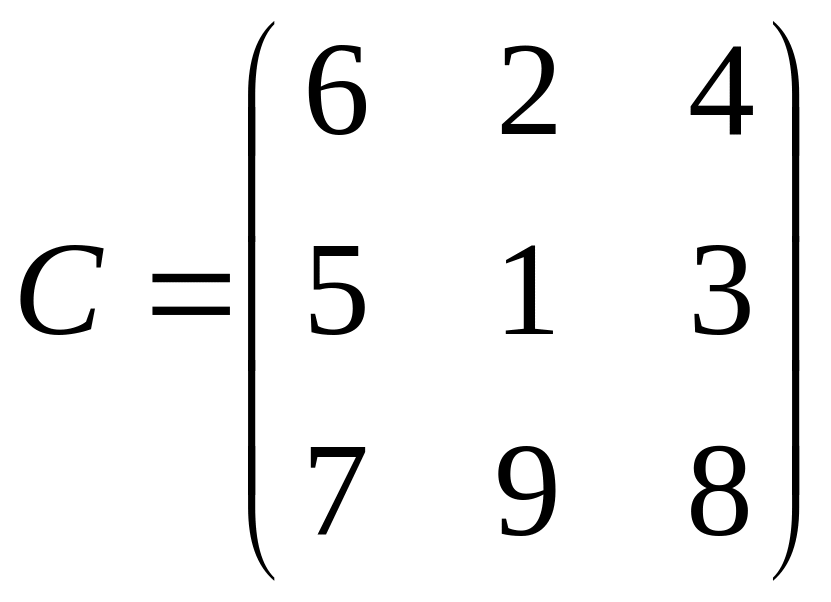 .
6.
.
6.
 .
7.
.
7.
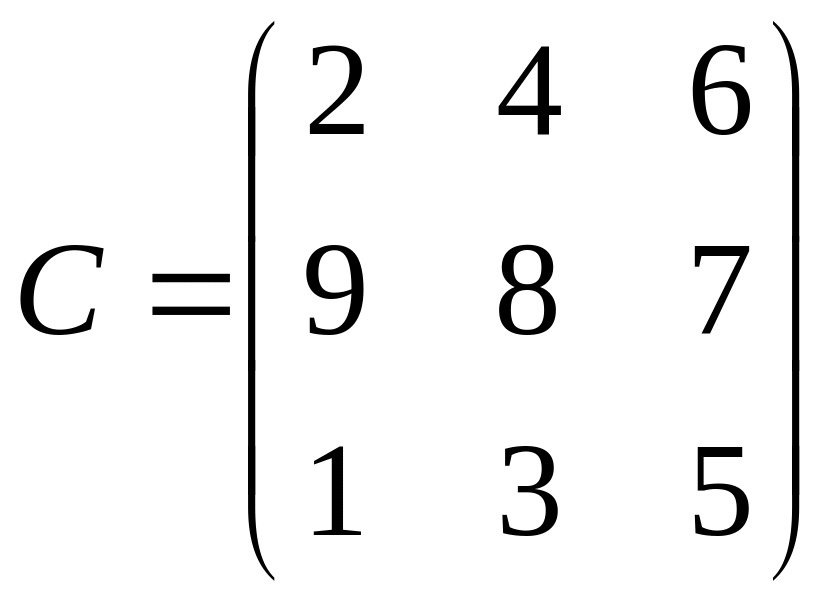 .
8.
.
8.
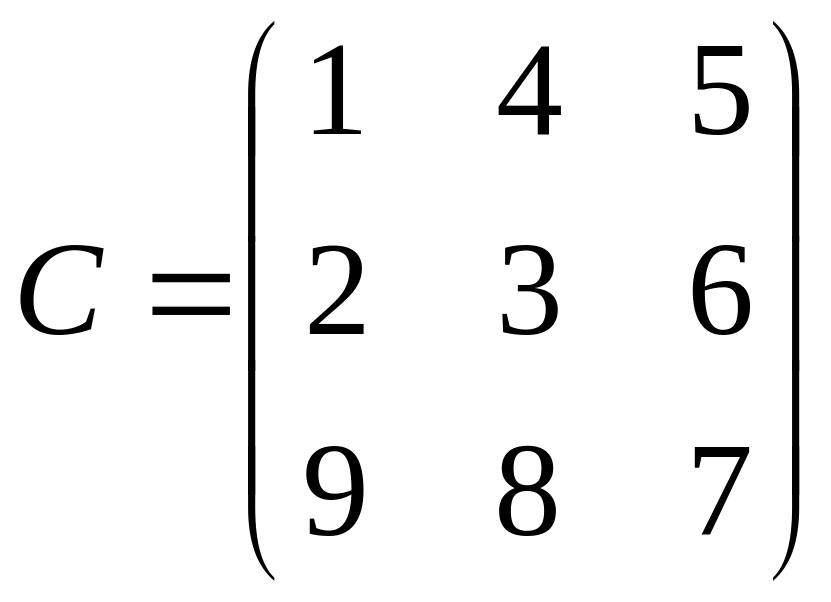 .
.
9.
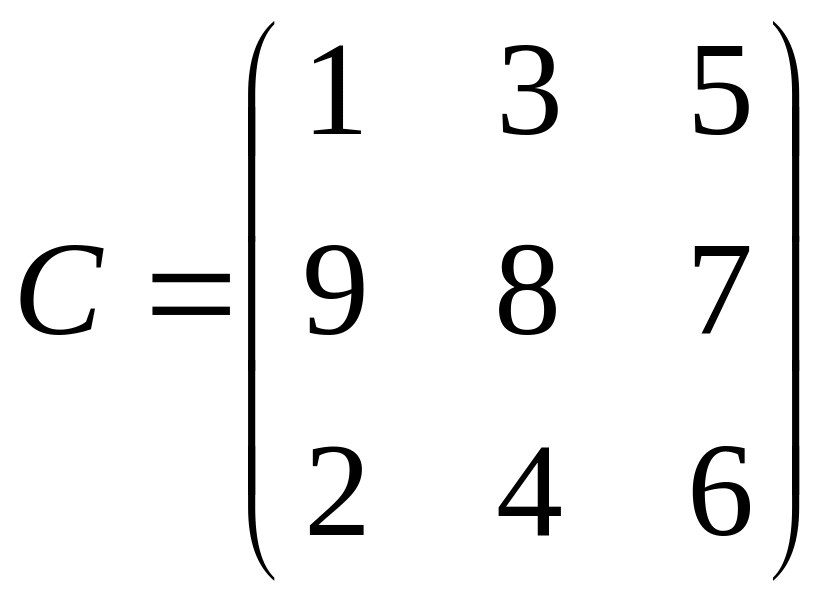 .
10.
.
10.
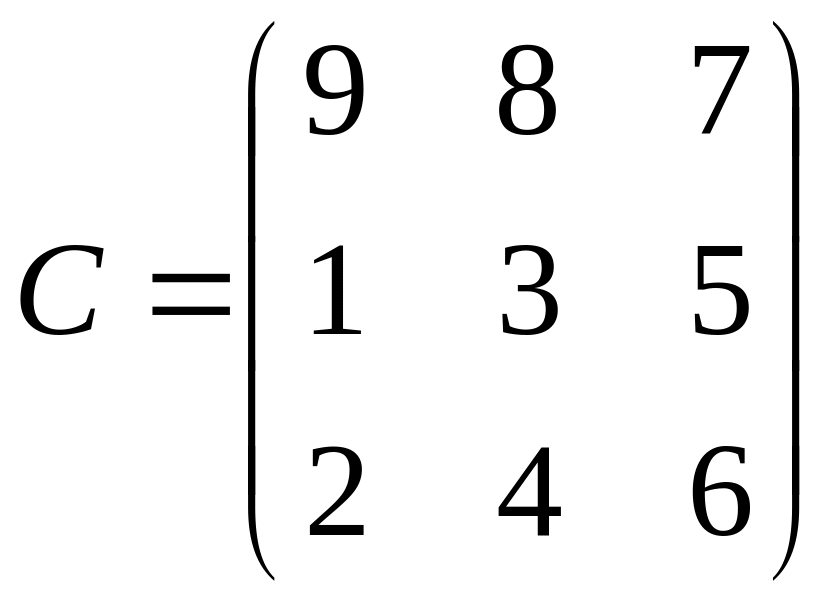 .
.
Задача 3. Проанализировать игру, используя принцип минимакса. Найти решение в смешанных стратегиях методами линейного программирования.
1.
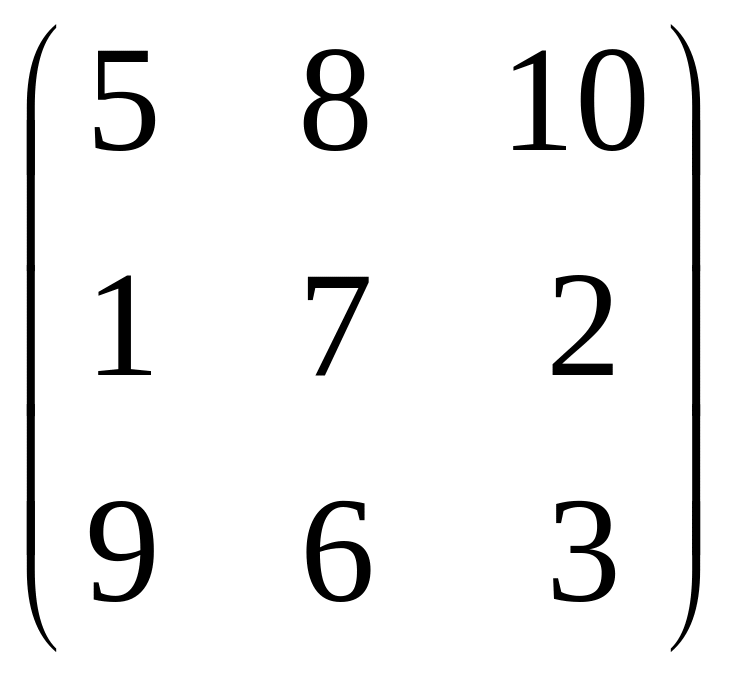 .
2.
.
2.
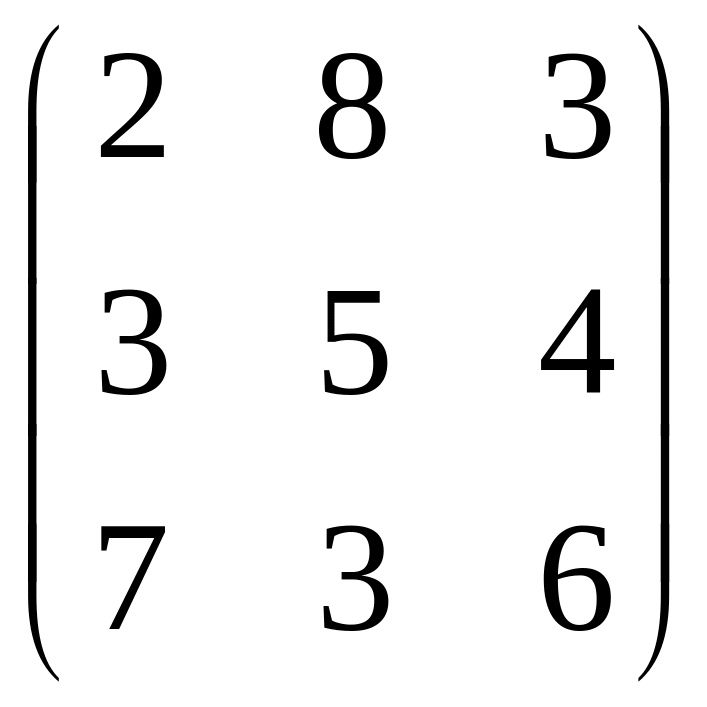 .
3.
.
3.
 .
4.
.
4.
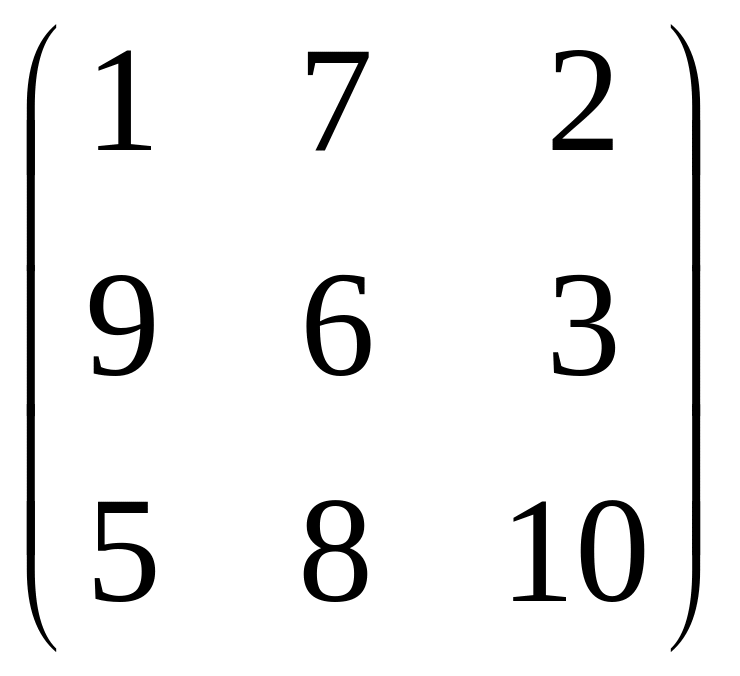 .
5.
.
5.
 .
.
6.
 .
7.
.
7.
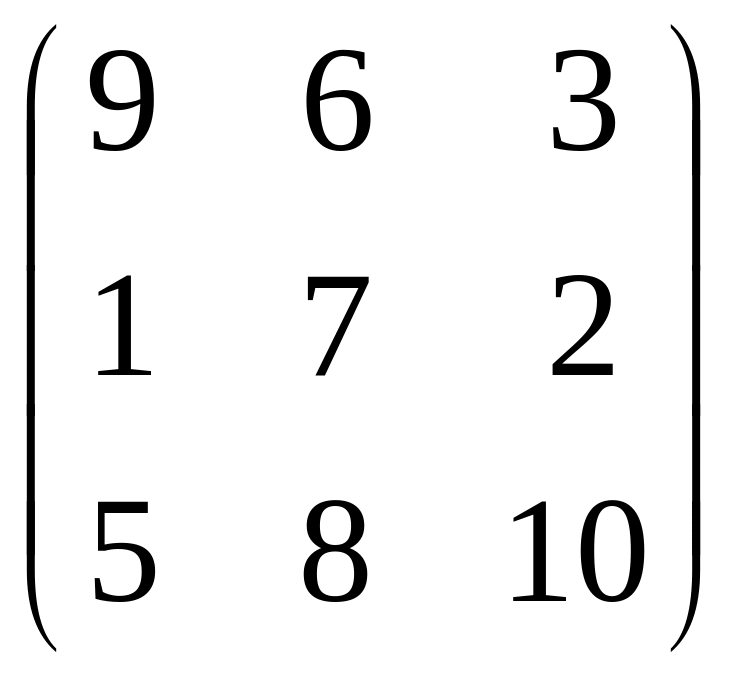 .
8.
.
8.
 .
9.
.
9.
 .10.
.10.
 .
.
Задача 4. Найти решение игр, определяемых следующими матрицами:
1.
![]() .
2.
.
2.
![]() .
3
.
3
![]() .
.
4.
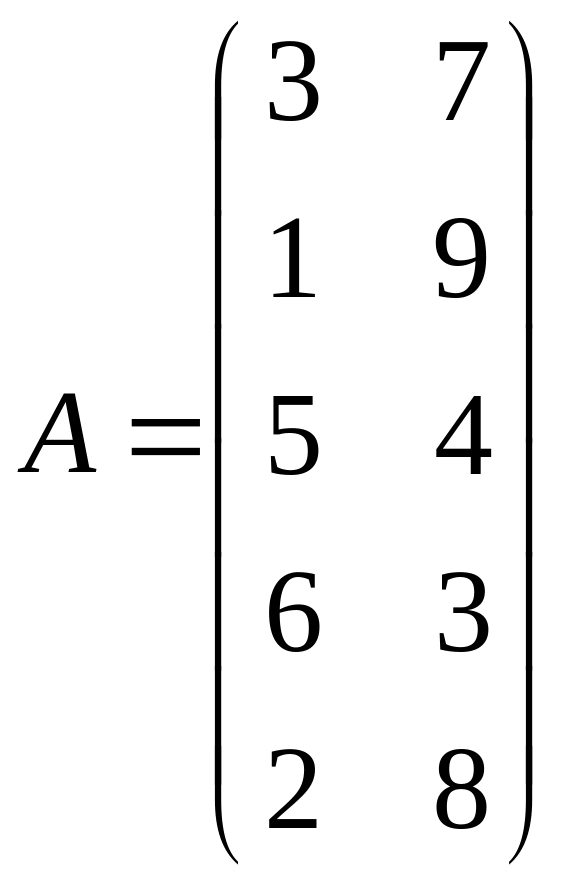 .
5.
.
5.
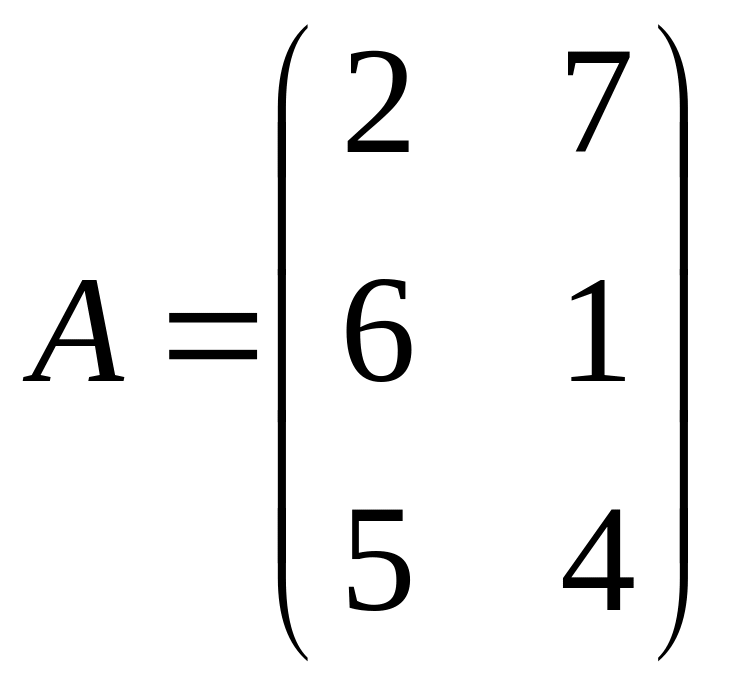 .
6.
.
6.
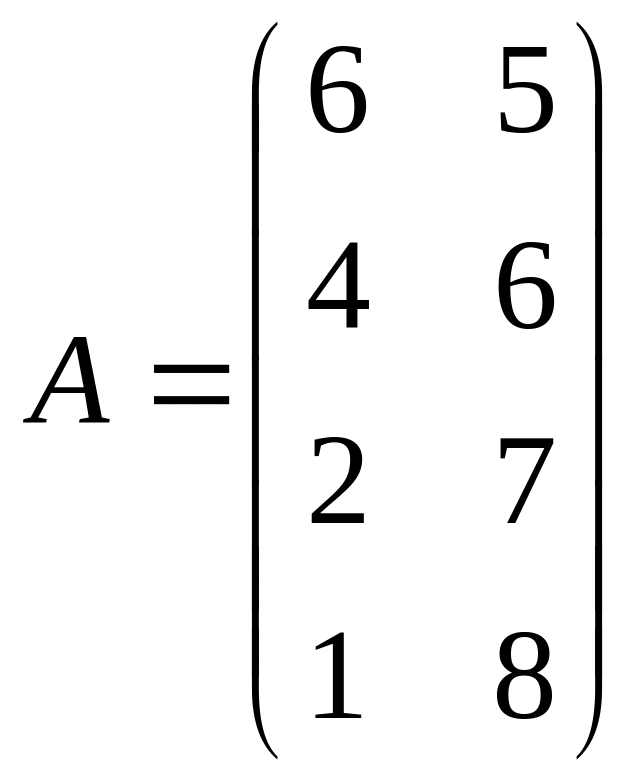 .
7.
.
7.
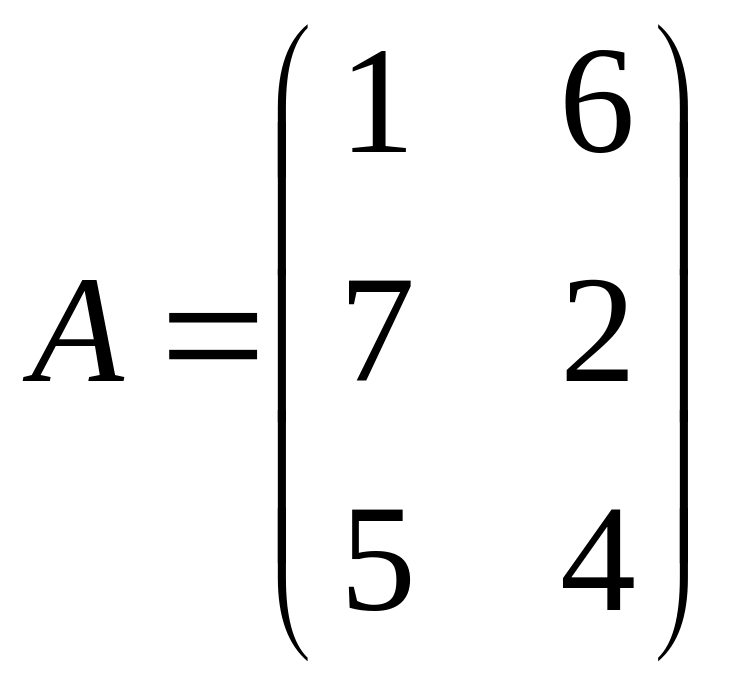 .
8.
.
8.
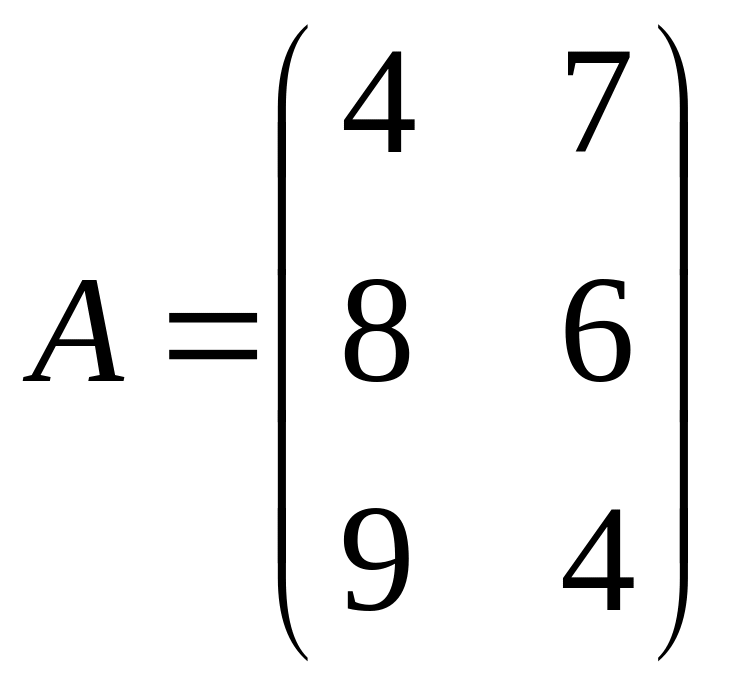 .
.
9.
![]() .
10.
.
10.
![]() .
.
