7. Задачи теории игр и линейное программирование.

Если имеется несколько сторон (лиц), каждая из которых принимает некоторое решение, определяемое заданным набором правил, и каждому из лиц известно возможное конечное состояние конфликтной ситуации с заранее определенными для каждой из сторон платежами, то говорят, что имеет место игра.

Пусть имеется два игрока, один из которых может выбрать тую стратегию из m своих возможных, а второй - тую стратегию из n своих возможных. В результате первый игрок выигрывает величину а второй ее проигрывает. Из чисел составим матрицу:

.

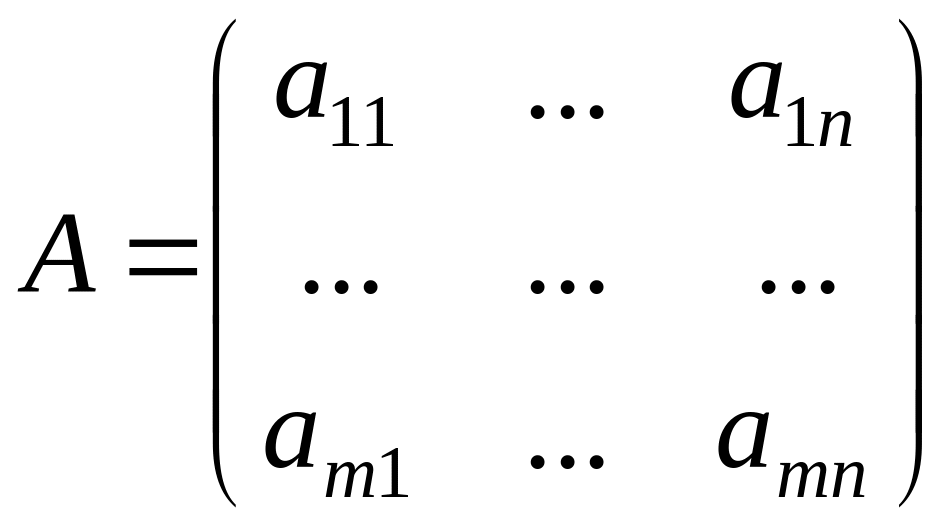Строки матрицы соответствуют стратегиям первого игрока, а столбцы – стратегиям второго. Эти стратегии называются чистыми.

Определение 1. Матрица А называется платежной матрицей игры.

Определение 2. Число называется нижней ценой игры, а число называется верхней ценой игры.

Определение 3. Если , то число v называется ценой игры.

Игра, для которой , называется игрой с седловой точкой.

Если игра, заданная матрицей, не имеет седловой точки, то для нахождения ее решения используются смешанные стратегии.

Определение 4. Вектор, каждая из компонент которого показывает относительную частоту использования игроком соответствующей чистой стратегии, называется смешанной стратегией данного игрока.

Из определения 4 следует, что сумма компонент указанного вектора равно единице, а сами компоненты не отрицательны. Обычно смешанную стратегию первого игрока обозначают как вектор , а смешанную стратегию второго – как вектор ., где , , , .

Если - оптимальная стратегия первого игрока, а - оптимальная стратегия второго игрока, то число

называется ценой игры.

Определение оптимальных стратегий и цены игры и составляет процесс нахождения решения игры.

Приведем примеры решения игр , и .

Пример 4. Найти решение игры, заданной матрицей и дать геометрическую интерпретацию этого решения.

Решение. Прежде всего проверим наличие седловой точки у данной матрицы. Для этого найдем минимальные элементы в каждой из строк (2 и 4) и максимальные элементы в каждом из столбцов (6 и 5).Значит, нижняя цена игры , а нижняя цена игры . Так как , то решением игры являются смешанные оптимальные стратегии, а цена игры заключена в пределах .

Предположим, что для игрока А стратегия задается вектором . Тогда при применении игроком В чистой стратегии или игрок А получит средний выигрыш, равный цене игры, т.е.

Помимо этих двух уравнений, добавляем уравнение связи . Решая полученную систему трех уравнений с тремя неизвестными, найдем , , .

Найдем теперь оптимальную стратегию для игрока В. Пусть для него стратегия задается вектором . Тогда

(1)

Решая полученную систему, найдем , .

Следовательно, решением игры являются смешанные стратегии , , а цена игры .

Дадим геометрическую интерпретацию данной игры. Для этого на плоскости введем систему координат и на оси отложим отрезок единичной длины , каждой точке которого поставим в соответствие некоторую смешанную стратегию (РИС.3).

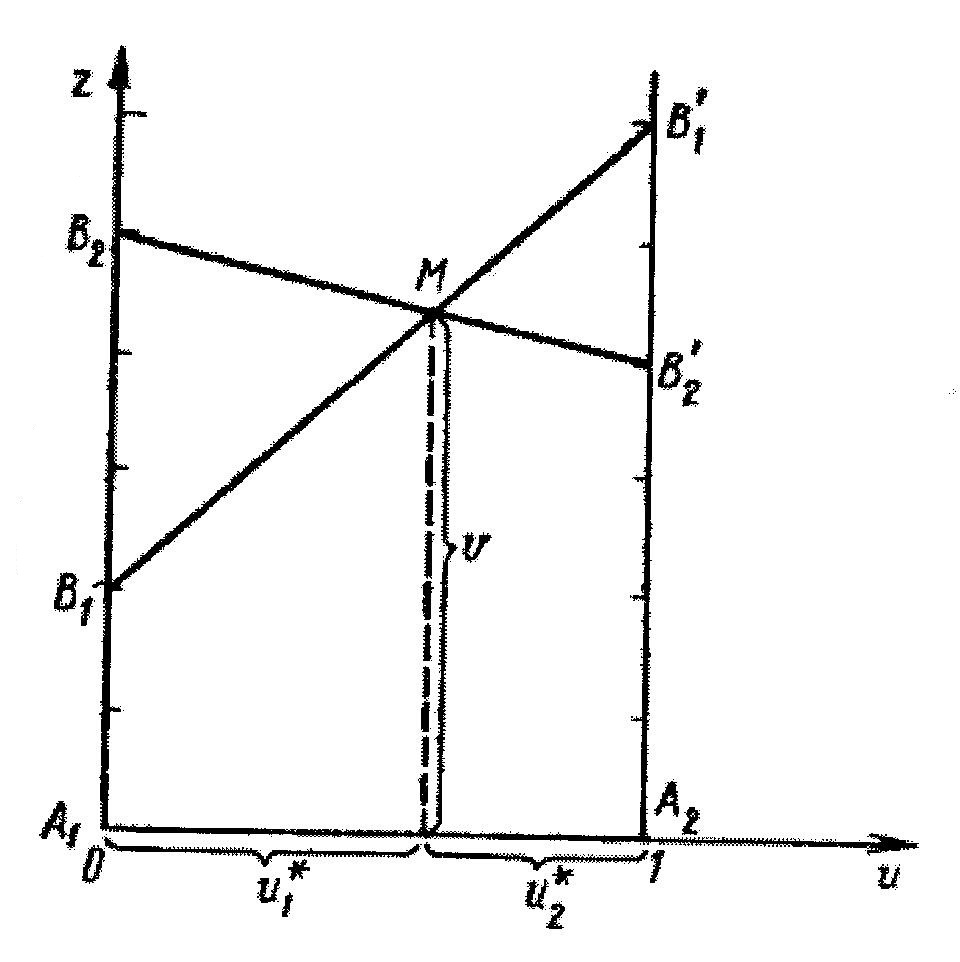
РИС 3.

В точках и восстановим перпендикуляры и на полученных прямых будем откладывать выигрыш игроков. На первом перпендикуляре (он совпадает с осью 0z) отложим выигрыш игрока А при стратегии А₁, а на втором – при стратегии А₂. Если игрок А применяет стратегию А₁, то его выигрыш равен 2 при условии, что игрок В применяет стратегию В₁, и равен 5 при условии, что игрок В применяет стратегию В₂. Числам 2 и 5 на оси 0z соответствуют точки В₁ и В₂. Если же игрок А применяет стратегию А₂, то его выигрыш равен 6 при условии, что игрок В применяет стратегию В₁, и равен 4 при условии, что игрок В применяет стратегию В₂. Эти два числа определяют точки и на перпендикуляре, восстановленном в точке А₂. Соединяя между собой точки В₁, В₂, и , получим две прямые, расстояние до которых от оси 0u определяет средний выигрыш при любом сочетании соответствующих стратегий. Таким образом, ординаты точек, принадлежащих ломаной определяют минимальный выигрыш игрока А при применении им любых смешанных стратегий. Эта минимальная величина является максимальной в точке M; следовательно, этой точке соответствует оптимальная стратегия , а ее ордината равна цене игры. Координаты точки М находим как координаты точек пересечения прямых и . Соответствующие три уравнения имеют вид:

Решая полученную систему, найдем , , .

Аналогично находится оптимальная стратегия для игрока В. Для ее определения мы имеем систему (1). Следовательно, решением игры являются смешанные стратегии , , а цена игры .

Обобщая изложенные выше результаты решения игры , можно указать основные этапы решения игры и .

1. Строят прямые, соответствующие стратегиям второго (первого) игрока.

2. Определяют нижнюю (верхнюю) границу выигрыша.

3. Находят две стратегии второго (первого) игрока, которым соответствуют две прямые, пересекающиеся в точке с максимальной (минимальной) ординатой.

4. Находят цену игры и оптимальные стратегии

Пример 5. Найти решение игры, заданной матрицей

.

Решение.

Н а рисунке прямые , и соответствуют стратегиям, а ломаная - нижней границе выигрыша игрока В. Игра имеет решение , , .

Пример 6. Найти решение игры, заданной матрицей

.

Решение.

Матрица имеет размерность . Строим прямые, соответствующие стратегиям игрока А:

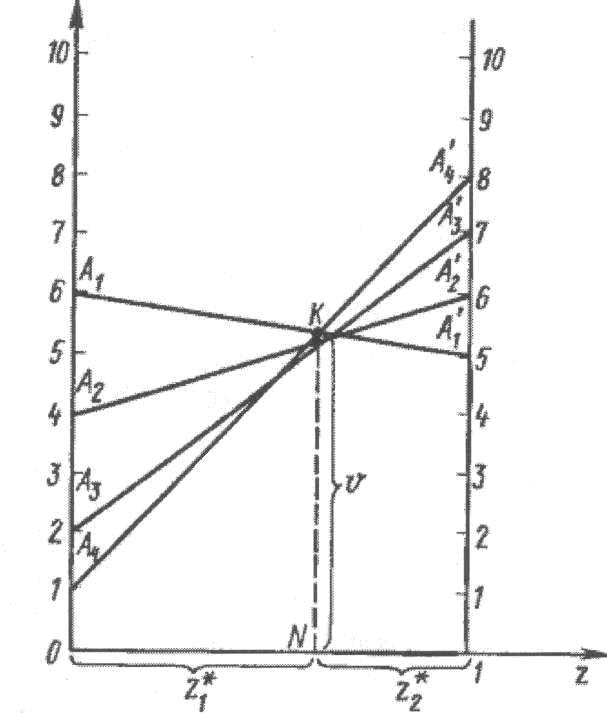
Ломаная соответствует верхней границе выигрыша игрока А, а отрезок NK – цене игры. Решение таково: , , .