ПРОИЗВОДНАЯ И ЕЁ ПРИМЕНЕНИЕ.

1. Приращение аргумента и приращение функции.

Рассмотрим график некоторой функции f.

Пусть x-произвольная точка, лежащая в некоторой окрестности фиксированной точки x₀. Разность х-х₀ называется приращением независимой переменной (или приращением аргумента) в точке х₀ и обозначается Δх: Δх=х-х₀.

Разность f(x)-f(x₀)=f(x0+Δx)-f(x₀) называется приращением функции в точке x₀, соответствующим приращению Δх аргумента, и обозначается Δf: Δf= f(x₀+ Δx)-f(x₀).

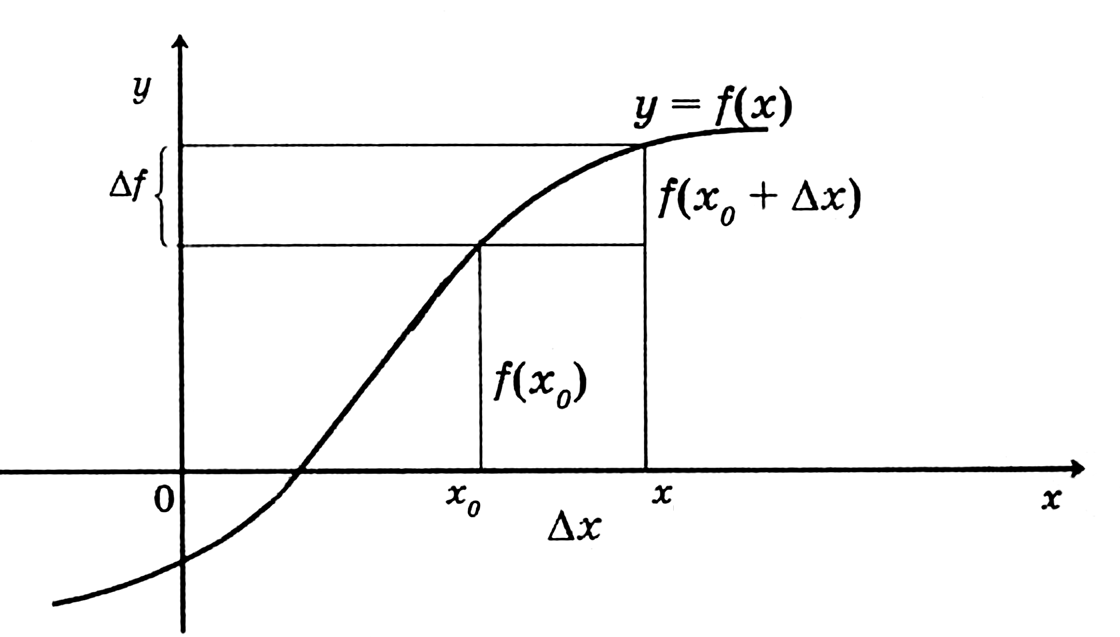
Рис.1

Пример: Дано: y=2x+5, x₀=3, Δx=0,2.

Найти Δf(x)

Решение: т.к. Δf(x)=f(x₀+Δx)-f(x₀)

1. f(x₀)=f(3)=2*3+5=11 f(x₀)=11

2. x₀+Δx=3+0,2=3,2

3. f(x₀+Δx)=f(3,2)=2*3,2+5=6,4+5=11,4 f(x₀+Δx)=11,4

4. Δf(x)=11,4-11=0,4 Ответ: 0,4

Из курса физики известно, что - средняя скорость за промежуток времени Δt, если Δt→0, то - мгновенная скорость. По аналогии в математике - скорость изменения функции, если Δx→0, то - скорость изменения функции в данной точке. Скорость изменения функции в данной точке назвали производной и обозначили f '(x₀) – (эф штрих от икс нулевого).

Определение: Производной функции f в точке x₀ называется предел отношения приращения функции к приращению аргумента, если Δx→0.

Нахождение производной в точке х₀ называют дифференцированием.(calculis differentialis-новое исчисление или разностное исчисление)

Определение: Функция, имеющая производную в некоторой точке, называется дифференцируемой в этой точке.

Производная - новая функция.

Пример1: f(x)=x². Найти f '(x).

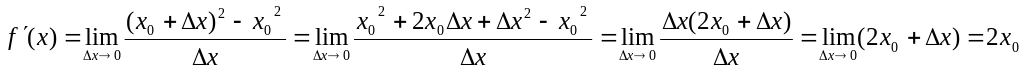
т.е.

Аналогично можно найти производные любых функций.

Для нахождения производных простейших функций существует таблица производных или формулы дифференцирования:

1. =0; с - постоянная. 2. 3. 4. 5. 6. 7.

8. 9. 10. 11. 12. = 13.

14. 15. 16. 17. 18.

Правила дифференцирования

Правило 1. Если функции v и u дифференцируемы в точке х, то их сумма дифференцируема в этой точке, причем производная суммы равна сумме производных:

Правило 2. Производная произведения двух функций u и v вычисляется по формуле:

Правило 3. Функция Сu, где С – постоянная, дифференцируема в точке x

´⁼ C u´

Правило 4. Частное функций u и v дифференцируемое в точке х, если v(x)≠0, и

Правило 5. Производная от сложной функции h(x)=q(f(x)) находиться по формуле:

т. е. производная сложной функции равна произведению производных ее составляющих.

Примеры.

1.y = x⁵, х⁴

2. y = 2x⁴+cosx-5, 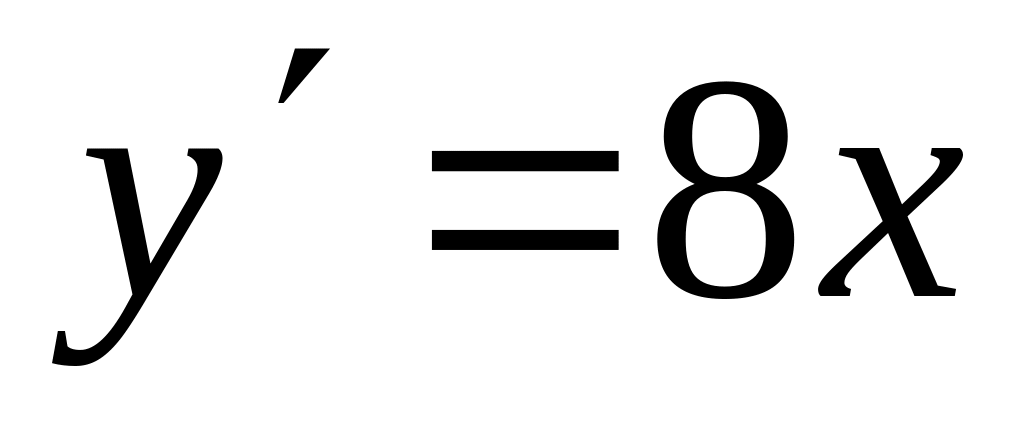³ – sinx.

ПРИМЕНЕНИЕ ПРОИЗВОДНОЙ

Пусть некоторый процесс описывается зависимостью y=f(x). Тогда производная функции f в точке х выражает скорость протекания указанного процесса. В этом состоит физический (механический) смысл производной.

,

Задача. Материальная точка движется прямолинейно по закону х(t)=t³-4t².Найти скорость движения и ускорение в момент времени t = 5c.

Решение.v(x)= ²-8t; v(5)=3*5²-8*5=35(м)

a(t) = a(5) = 6*5-8=30 – 8 = 22(м\с²)

Ответ: v = 35м\с; а = 22м\с².

.