
- •33. Електричний струм в газах і вакуумі несамостійний і самостійний розряди в газах. Поняття про плазму. Термоелектронна емісія вакуумні прилади.
- •35. Електронно-дірковий перехід. Напівпровідниковий діод. Транзистор. Напівпровідникові прилади та їх застосування.
- •37. Дія магнітного поля на провідник зі струмом. Сила Ампера. Робота при переміщенні провідників у магнітному полі потік магнітної індукції.
- •Третє рівняння Максвелла[ред. • ред. Код]
- •38. Пара, діа- та феромагнетики.
- •39. Сила Лоренца. Рух зарядів у магнітних полях.
39. Сила Лоренца. Рух зарядів у магнітних полях.
39. Си́ла Ло́ренца — сила, що діє на електричний заряд, який перебуває у електромагнітному полі.
![]() .
.
Тут ![]() —
сила,
—
сила, ![]() —
величина заряду,
—
величина заряду, ![]() — напруженість
електричного поля,
— напруженість
електричного поля, ![]() — швидкість руху
заряду,
— вектор
магнітної індукції[1].
Іноді силою Лоренца називають лише
другу складову цього виразу — силу, яка
діє на заряд, що рухається, з боку
магнітного поля (
— швидкість руху
заряду,
— вектор
магнітної індукції[1].
Іноді силою Лоренца називають лише
другу складову цього виразу — силу, яка
діє на заряд, що рухається, з боку
магнітного поля (![]() ).
).
Електричне поле діє на заряд із силою, направленою вздовж силових ліній поля. Магнітне поле діє лише на рухомі заряди. Сила дії магнітного поля перпендикулярна до силових ліній поля й до швидкості руху заряду.
Сила Лоренца перпендикулярна до площини в якій лежать B і v і створює доцентрове прискорення, внаслідок чого заряджена частина рухається по коловій орбіті. Fл = F Fл = Bvq F = maдоц. ; aдоц. = v²/r Bvq = mv²/r => r = mv/Bq - радіус орбіти по якій рухається заряд в магнітному полі. r ~ v а). Якщо α = 90°, заряд рухається по колу з радіусом r. б). Якщо α відмінне від 90°, то заряд рухається по спіралі. h = v2T ; h = крок ; T = період.
І.
Описати
рух зарядженої частинки, напрям швидкості
якої утворює гострий кут із
![]() .
.
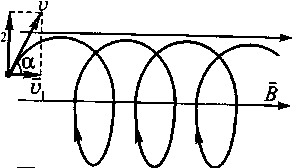 Зобразимо
вектори v
і В. Нехай
швидкість
напрямлена під кутом а
до
вектора В
(див.
рис. 1). Розкладемо v
на
складові
Зобразимо
вектори v
і В. Нехай
швидкість
напрямлена під кутом а
до
вектора В
(див.
рис. 1). Розкладемо v
на
складові![]() і
v2
-
паралельну і перпендикулярну до В.
Складова
v2
зумовлює
виникнення сили Лоренца:
Fn
= qv2B,
що
надає зарядженій частинці
доцентрового прискорення.
і
v2
-
паралельну і перпендикулярну до В.
Складова
v2
зумовлює
виникнення сили Лоренца:
Fn
= qv2B,
що
надає зарядженій частинці
доцентрового прискорення.
Тоді
отримаємо:
![]() або
або
![]()
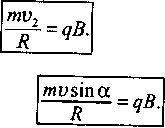
Оскільки
![]() ,
то матимемо:
,
то матимемо:
З цієї формули можна знайти m,v,R,q i B.
П![]() еріод
обертання визначають так:
еріод
обертання визначають так:
З![]() формули (1) отримаємо:
формули (1) отримаємо:![]() ,
тоді:
,
тоді:
![]()
За час Т частинка пролітає у напрямі вектора індукції В таку відстань
Отже,
частинка рухається по гвинтовій лінії,
крок якої
![]() ,
а радіус
становить:
,
а радіус
становить:![]()
