Вопрос 10-13.
Презентация
Вопрос 14. Измерение центральной тенденции (мода, медиана, среднее значение).
Измерение ЦТ представляет собой определение такого показателя, который наиболее ярко, наилучшим образом отображает все значения признаков.
Средняя арифметическая простая (для неструктурированных данных):
Средняя арифметическая взвешенная (для структурированных данных):
X - значение признака, n - количество значений, f - частота.
Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда.
В ранжированных рядах несгруппированных данных для нахождения медианы сводятся к поиску порядкового номера медианы. Медиана может быть вычислена по следующей формуле:
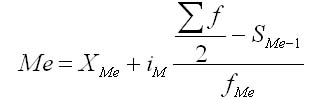
Где:
Хm — нижняя граница медианного интервала;
im — медианный интервал;
Sme— сумма наблюдений, которая была накоплена до начала медианного интервала;
fme — число наблюдений в медианном интервале.
Свойства медианы:
Медиана не зависит от тех значений признака, которые расположены по обе стороны от нее.
Аналитические операции с медианой весьма ограничены, поэтому при объединении двух распределений с известными медианами невозможно заранее предсказать величину медианы нового распределения.
Медиана обладает свойством минимальности. Его суть заключается в том, что сумма абсолютных отклонений значений х, от медианы представляет собой минимальную величину по сравнению с отклонением X от любой другой величины
Графическое определение медианы
Для определения медианы графическим методом используют накопленные частоты, по которым строится кумулятивная кривая. Вершины ординат, соответствующих накопленным частотам, соединяют отрезками прямой. Разделив пополам последнюю ординату, которая соответствует общей сумме частот и проведя к ней перпендикуляр пересечения с кумулятивной кривой, находят ординату искомого значения медианы.
Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения.
Нахождение моды часто сводится к выбору признака с наибольшей частотой. В интервальном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле:
Где:
ХМо — нижняя граница модального интервала;
imo — размах модального интервала;
fм0, fм0-1,, fм0+1 - частоты в модальном, предыдущем и следующем за модальным интервалах.
Модальный интервал определяется по наибольшей частоте.
Вопрос 15. Измерение вариации признака (размах, квартильный размах, дисперсия, стандартное отклонение, коэффициент вариации).
Размах вариации - мера разброса значений выборки, определяемая как разность между максимальным и минимальным значениями.
Квартильный размах - 25% значений.
Квартиль - вариант, который делит численность ряда на 4 равные части.
Дисперсия представляет собой средний квадрат отклонений значений признака от средней арифметической.
Стандартное отклонение - квадратный корень из дисперсии.
Это значение можно представить как среднее расстояние, на котором находятся элементы от среднего элемента выборки. Короче, чем оно меньше, тем лучше среднее значение характеризует всю выборку.
