Преподаватель __________________

Рисунок 14 – Рекомендуемая форма протокола лабораторной работы № 4

Лабораторная работа № 5

ОПРЕДЕЛЕНИЕ КОЭФФИЦИЕНТА расхода при ИСТЕЧЕНИи ЧЕРЕЗ НАСАДКИ

Общие сведения

Расход жидкости при истечении через отверстия и насадки определяется формулой, которая выводится из уравнения Бернулли и имеет вид

(13),

где: - площадь проходного сечения отверстия (или насадка);

- коэффициент расхода, равный произведению коэффициента сжатия струи на коэффициент скорости , т.е. .

- расчетный напор, под действием которого происходит истечение.

В общем случае расчетный напор включает разность нивелирных высот и разность пьезометрических высот , т.е.

.

Физический смысл коэффициента расхода - это отношение действительного расхода жидкости к расходу той же жидкости при отсутствии сжатия струи ( ) и сопротивления ( ): .

Численное значение коэффициента расхода зависит, прежде всего, от геометрических параметров отверстия или насадка, а также от числа Рейнольдса. В некоторых случаях значение резко меняется при изменении напора в связи с изменением режима истечения.

Приведем основные сведения по истечению через насадки, представленные на рис. 15:

а) Насадок, имитирующий круглое отверстие в тонкой стенке (отверстие с острой кромкой). Для этого случая характерно значительное сжатие струи и малое сопротивление. Низкое значение коэффициента расхода обусловлено сжатием струи.

б) Внешний цилиндрический насадок (сверление в толстой стенке), первый (безотрывный) режим истечения. Внутри насадка струя сужается, а затем расширяется, и из насадка вытекает полным сечением, следовательно, и . Кольцевое пространство вокруг струи заполнено вихрем. Вследствие сужения и последующего расширения струи, внутри насадка при истечении в атмосферу возникает вакуум ( ). Чем больше напор , под действием которого происходит истечение, тем меньше абсолютное давление в суженном сечении струи. При некотором критическом напоре это давление делается примерно равным давлению насыщенных паров воды, и режим истечения меняется.

в) Внешний цилиндрический насадок при втором режиме истечения, когда струя после сужения не расширяется, а перемещается внутри насадка, не соприкасаясь с внутренней его поверхностью. Второй режим истечения ничем не отличается от истечения через отверстия в тонкой стенке, и коэффициент имеет те же значения.

г) Внешний цилиндрический насадок с коническим входом. Устройство конуса на входе существенно улучшает гидравлические свойства насадка: уменьшаются или исчезают завихрения при входе в цилиндрическую часть, уменьшается сопротивление, повышается коэффициент расхода по сравнению с цилиндрическим насадком без конического входа, исключается отрыв потока от стенок насадка.

Цель, методика и обработка результатов эксперимента

Цель работы заключается в опытном определении коэффициента расхода для четырех указанных выше характерных случаев истечения.

Экспериментальная установка (рисунок 15) состоит из бака Б, к которому подводится вода через регулировочный кран Р. В дно бака выставляют те или иные насадки. Давление в баке р_м измеряется манометром М. Так как манометр установлен непосредственно перед насадком, а истечение происходит в атмосферу, то р_м = ∆р, а ∆z = 0.

Расход измеряется с помощью мерного бака (Подробнее об используемом методе выбора и измерения величины расхода смотрите «Общие указания …» (стр. 3)).

Порядок проведения эксперимента:

- установите в бак насадок, для чего при А = 0 подведите курсор к выбранному насадку и щелкните левой кнопкой мыши;

- задайте расход путем установки определенного значения А в окне «открытие крана»;

- зафиксируйте показания манометра р_м.;

- замерьте расход.

Задавая значение А от 0,2 до 1 занесите в протокол величины р_м и Q для каждого значения А.

Величину коэффициента μ определить по формуле: ,

где S_o – площадь проходного сечения отверстия в насадке, принимается одинаковой для всех насадков.

Проведите эксперимент и определите значение μ для всех типов насадков.

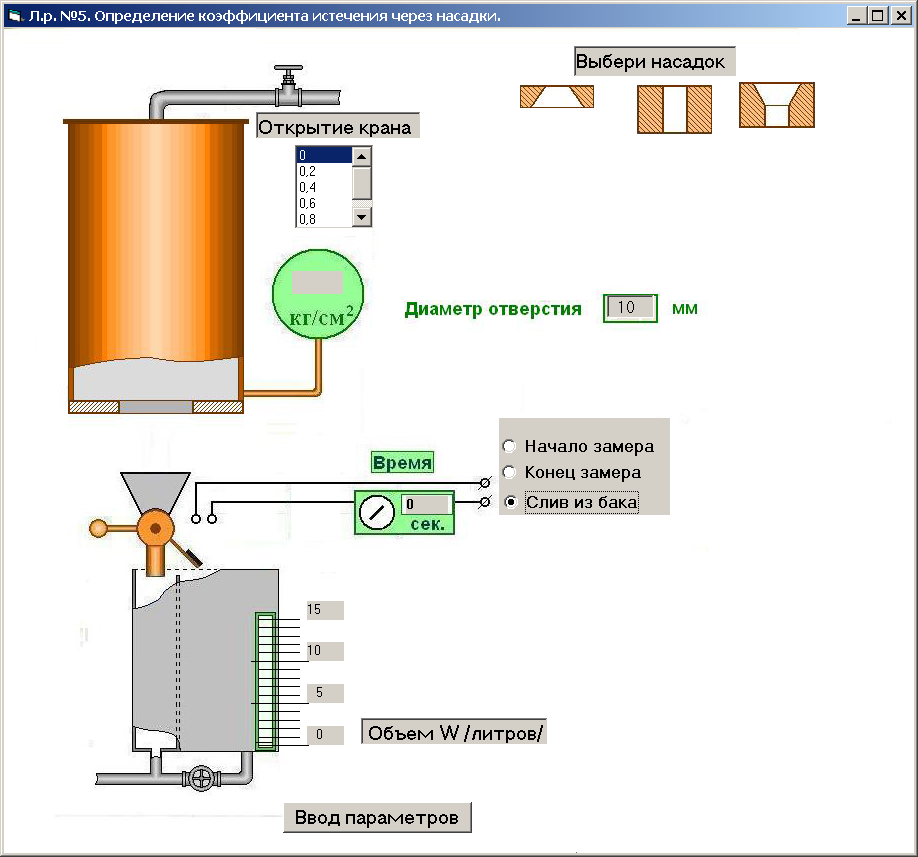
Рисунок 15 – Схема лабораторной установки

Требования к оформлению отчета по лабораторной работе

Рекомендуемая форма протокола к лабораторной работе № 5 представлена на рис. 16.

При оформлении протокола в левом столбце таблицы следует от руки нарисовать характер истечения жидкости через насадок в рассматриваемом режиме.

ПРОТОКОЛ

лабораторной работы №5

ОПРЕДЕЛЕНИЕ КОЭФИЦИЕНТА РАСХОДА ПРИ ИСТЕЧЕНИИ ЧЕРЕЗ НАСАДКИ

Диаметр проходного сечения отверстия насадка d ___10______ мм

Тип насадка, характер истечения	рм кгс/см2	W л	t c	Q см3/с	μ
Безотрывное истечение
Истечение с отрывом

Студент____________________ Группа__________________

Преподаватель_________________

Рисунок 16 – Рекомендуемая форма протокола лабораторной работы № 5

Лабораторная работа № 6

ГИДРАВЛИЧЕСКИЙ УДАР В ТРУБОПРОВОДЕ

Общие сведения

Гидравлическим ударом называется колебательный процесс, возникающий в трубопроводе при внезапном изменении в нем скорости течения жидкости.

Чаще всего гидравлический удар возникает в случае резкого торможения потока жидкости, например, вследствие быстрого закрытия крана или клапана. В начальный момент при этом возникает значительное, скачкообразное возрастание давления на величину , кинетическая энергия потока переходит в работу упругих деформаций жидкости и стенок трубы - жидкость сжимается, а стенки трубы растягиваются.

Проф. Н.Е. Жуковский вывел формулу для определения величины ударного давления , приравняв кинетическую энергию всего потока жидкости в трубе до внезапной ее остановки сумме двух работ - работе сжатия жидкости и работе растяжения стенок трубопровода.

Формула Жуковского имеет следующий вид (для случая полного торможения потока):

, (14)

где: - плотность жидкости;

- начальная скорость потока, которая внезапно уменьшилась до нуля;

- скорость распространения ударного давления (ударной волны) по трубопроводу.

Эта скорость по Жуковскому определяется по следующей формуле:

, (15)

где: – объемный модуль упругости жидкости;

– линейный модуль упругости материала стенок трубы;

– внутренний диаметр трубы;

– толщина стенок трубы.

Для абсолютно жесткого трубопровода вторая дробь под радикалом в формуле (15) обращается в ноль, а скорость ударной волны оказывается равной скорости распространения звука в жидкости, т.е.:

.

Таким образом, малая сжимаемость капельных жидкостей и высокая жесткость металлических труб и является причиной возникновения большого ударного давления . В гибких шлангах (рукавах), а также в газопроводах, гидравлический удар ничтожно мал благодаря малой жесткости материала стенок и большой сжимаемости среды.

Приведенная выше формула Жуковского (14) справедлива лишь при достаточно быстром закрытии крана, или, точнее говоря, когда время закрытия

,

где - фаза гидравлического удара - это время, необходимое для прохождения ударной волны от крана до начала трубопровода длиной и обратно.

При ударное давление получается существенно меньше, чем по формуле (14), так как в момент подхода фронта отраженной ударной волны к запорному устройству, оно, будучи не полностью закрытым, пропускает через себя некоторое количество жидкости, смягчая этим удар.