
- •Лекция 1. Основные понятия теории вероятности. (тв)- сс-1
- •Лекция 2. Основные теоремы теории вероятности. Сс-2
- •6). Произведение противоположных событий, есть невозможное событие. Вероятность произведения событий.
- •Лекция 3 Основные теоремы теории вероятности. Сс-3
- •Лекция 4. Случайные величины. Св-1.
- •Дискретные св.
- •Числовые характеристики случайных величин.
Лекция 3 Основные теоремы теории вероятности. Сс-3
Формула полной вероятности.
Пусть появление некоторого события А возможно лишь при наступлении одного n из попарно несовместных событий Вi, образующих полную группу и называемых гипотезами.
Тогда вероятность события А равна сумме попарных произведений вероятности каждой из этих гипотез Вi на соответствующую условную вероятность появления события А.
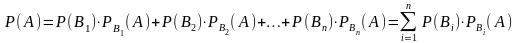
Формулы Байеса.
Пусть появление в некотором испытании события А возможно лишь при наступлении одного n из попарно несовместных событий Вi, образующих полную группу и называемых гипотезами.
Тогда, зная вероятности гипотез Р(Вi) до проведения испытания, мы можем переоценить их после проведения испытания, в результате которого появилось событие А.
![]() ,
,
где
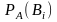 - вероятности гипотез, вычисленные
после проведения испытания, при условии,
что событие А произошло (апостериорные
вероятности гипотез);
Р(А) – полная вероятность события А,
- вероятности гипотез, вычисленные
после проведения испытания, при условии,
что событие А произошло (апостериорные
вероятности гипотез);
Р(А) – полная вероятность события А,
Р(Вi) – вероятности гипотез, известные до испытания (априорные вероятности гипотез),
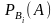 —
вероятность
наступления события А при истинности
гипотезы Вi.
—
вероятность
наступления события А при истинности
гипотезы Вi.
Теорема Байеса — одна из основных теорем элементарной теории вероятностей, которая определяет вероятность наступления события в условиях, когда на основе наблюдений известна лишь некоторая частичная информация о событиях. По формуле Байеса можно более точно пересчитывать вероятность, принимая во внимание как ранее известную информацию (априорные данные), так и данные новых наблюдений (апостериорные данные).
Вычисление вероятностей событий в серии независимых испытаний.
Схема Бернулли - последовательность независимых испытаний (т.е. таких испытаний, вероятность исходов которых не зависит ни от номера испытания, ни от результатов предшествующих испытаний) с двумя возможными исходами. Вероятность первого исхода - А, называемого успехом, в каждом испытаний равна р, тогда вероятность второго исхода – неуспеха, равна разности единицы и р : Р(А)=р Р( )=1-р=q.
Формула Бернулли
Вероятность, что в серии из n испытаний по схеме Бернулли ,событие А, произойдёт ровно k раз:
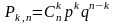 ,
где
,
где
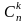 число
сочетаний из “n”
элементов по “k”
элементов в каждом.
число
сочетаний из “n”
элементов по “k”
элементов в каждом.
р – вероятность
наступления события А в одном испытании,
 –вероятность не наступления события
А в одном испытании, n
– общее число испытаний, k
– число успехов в серии из n
испытаний.
–вероятность не наступления события
А в одном испытании, n
– общее число испытаний, k
– число успехов в серии из n
испытаний.
Теорема Лапласа: применяется при больших значениях n, когда формулу Бернулли использовать сложно.
Пусть Р(А)=р – вероятность проявления события А в одном испытании,
тогда вероятность, что в серии из n независимых испытаний событие А произойдёт точно k раз приблизительно вычисляется по формуле Лапласа:
 ,
где
,
где
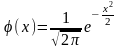 ;
где
;
где
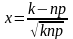 ,
,
 .
.
Интегральная
теорема Лапласа. –
позволяет определить вероятность того,
что событие А в n
независимых испытаниях произойдёт не
менее
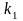 и
не более
и
не более![]() раз.
раз.
 ,
где
,
где
 ,
,
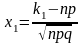 ;
;
![]()
Значения функций
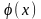 и
и
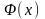 приводятся в таблицах (см тб. 1 и 2)
приводятся в таблицах (см тб. 1 и 2)
Закон Пуассона распределения вероятностей массовых и редких событий.
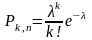 -вероятность того,
что в серии из n
испытаний «успех» произойдёт ровно k
раз.
-вероятность того,
что в серии из n
испытаний «успех» произойдёт ровно k
раз.
где
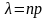 ,
n
– общее число независимых испытаний,
р – вероятность «успеха» в одном
испытании.
,
n
– общее число независимых испытаний,
р – вероятность «успеха» в одном
испытании.
Формула Пуассона применяется, когда n – очень велико, а р – достаточно мало.
