Лекция 1. Основные понятия теории вероятности. (тв)- сс-1

ТВ – это раздел математики изучающий закономерности случайных явлений. «ТВ объединяет точность математических доказательств с неопределённостью случая и примеряет эти противоречивые элементы».

Испытание - модель реального действия, реализация определённого комплекса условий, который может быть воспроизведён сколько угодно раз. Задать испытание в т/в это значит задать множество его элементарных (неделимых на более мелкие) исходов . = .

Случайное событие - событие которое может наступить или не наступить в результате испытания. Для любого события “А” множество  элементарных событий разделяется на два подмножества  : А⁺ и А^– .

А^{+ -} подмножество благоприятных исходов вместе с каждым из которых наступает событие А⁺.

А^{– -} подмножество неблагоприятных исходов, при реализации которых событие А не происходит.

Задать событие– это значит задать подмножество А⁺ благоприятных исходов на множестве .

Невозможное событие - событие которое никогда ни происходит в результате испытания. Достоверное событие - событие которое всегда происходит при испытании.

Два события называются несовместными, если появление одного исключает появление другого.

События совместны, если они могут произойти одновременно.

Вероятность случайного события- это количественная мера степени уверенности в его наступлении.

Классическое определение вероятности: Для испытания с конечным числом равновозможных исходов вероятность случайного события “A” обозначается Р(А) и определяется как отношение числа благоприятных исходов m к общему числу n элементарных исходов испытания:

Р(А) = m/n.

Вероятность случайного события принимает значения от 0 до 1. 0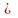 Р(А) 1

Вероятность невозможного события равна 0. Вероятность достоверного события равна 1.

Статистическое определение вероятности.

Относительная частота события А - отношение числа наступления события А в серии из n испытаний к общему числу испытаний n.

Если в различных сериях из n испытаний относительная частота m(А)/n события мало изменяется и близка некоторому числу Р , то это число считают статистической вероятностью.

Геометрическое определение вероятности - Применяется к испытанию с бесконечным числом равновозможных исходов. Пусть дан отрезок длины “L” и на нём отрезок “L₁” Под геометрической вероятностью принимается вероятность попадания точки на отрезок L₁, равная отношению длин этих отрезков Р(А) = ^L1/_L

Элементы комбинаторики:

Комбинаторика – это раздел математики в которой изучаются расположения (комбинации) объектов составленные по определённым правилам и способам подсчёта этих комбинаций.

Основными расположениями объектов являются: перестановки размещения и сочетания.

Основное правило комбинаторики: если элемент а₁ можно выбрать “n₁” способами и при каждом таком выборе, выбор элемента а₂ может быть произведён n₂ способами, то общее число пар (а₁;а₂) равно N = n₁۰n₂.

Перестановками называют упорядоченное множество составленное из всех элементов “A”. Перестановки отличаются друг от друга порядком элементов.

Р_n – число перестановок множества из n элементов = n۰(n – 1)۰(n – 2)…1 = n!; (0! = 1; 1! = 1; 2! = 2; 3! = 6…).

Размещения. A_n^k упорядоченные k- элементные подмножества n элементного множества.

Число размещений : A_n^k=n(n-1)(n-2)۰…۰(n – k + 1)=

Сочетания C_n^{k -}“k” элементные подмножества “n” элементного множества. Два сочетания отличаются друг от друга только составом элементов, но не их порядком.

Связь между числом сочетаний , размещений и перестановок. A_n^k = C_n^k۰P_k

Число сочетаний: C_n^k =A_n^k/P_k =

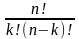
Свойства числа сочетаний: 1). C_n^k = C_n^{n – k}; 2). C_n^k = C_{n – 1} ^{k – 1} + C ^k _{n – 1}