2. Лінійна (аперіодична) згортка дискретних сигналів

Нехай і - відповідно кінцеві - точечні й - точечні дискретні сигнали. Лінійною (аперіодичною) згорткою цих сигналів називається дискретний сигнал, що визначається як послідовність

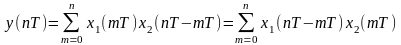. (2.13)

Очевидно, що має довжину .

Алгоритм обчислення кругової згортки може бути застосований також для обчислення лінійної згортки. З цією метою належить перейти від дискретних сигналів і до -точечних сигналів і , та доповнити послідовність і відповідним числом нульових відліків. Після обчислення у - точках ДПФ і знайти їх добуток ДПФ = · і, згідно з формулою (2.10), обчислити згортку .

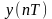2.6. Z - перетворення

1. Пряме z - перетворення

Формальним обґрунтуванням застосування Z - перетворення є те, що це перетворення допускає такі ж алгебраїчні дії над різницевими рівняннями, що й перетворення Лапласа над диференційними рівняннями. Однобічне Z - перетворення послідовності , =0,1,2,... обумовлене рядом

, (2.14)

де - комплексна змінна, а - функція цієї комплексної змінної (рис.2.7), тобто .

Оскільки (2.14) – ступеневий ряд змінної z^-1, то, як правило, виникає питання про збіжність такого ряду.

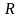Ряд (2.14) збігається для | й розбігається для , де радіус збіжності є верхньою межею послідовності .

Приклад 4. Нехай

.

Тоді

. (2.15)

Якщо величина то вираз являє собою нескінченно спадну геометричну прогресію, сума якої визначається за формулою

, (2.16)

де - знаменник геометричної прогресії.

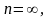
У прикладі (4) ; - перший член геометричної прогресії,

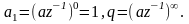
Зона збіжності тут визначається радіусом кола у Z -площині, поза якою не має особливих точок.

2.6.2.Властивості z - перетворення

Наведемо приклади важливих та широко використовуваних властивостей і теорем Z - перетворення, що виходять із визначення (2.14) або легко доводяться.

1. Лінійність

Якщо послідовності 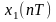i мають відповідно Z - перетворення 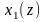i , і – постійні коефіцієнти, що не залежать від , то вираз 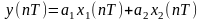має Z - перетворення: .

2. Зсув послідовності

Якщо і при , то має Z - перетворення:

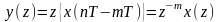. (2.16)

Приклад 5. Нехай , і . При цьому з прикладу (4) , тоді за формулою (2.16) .

3. Згортка послідовностей

Нехай .

Згортка послідовностей i має Z - перетворення , що дорівнює добутку і : .

2.6.3. Обернене z - перетворення

За визначенням, є оберненим Z - перетворенням від . Його можна знайти за формулою (2.14) з допомогою інтегральної теореми Коші. Спочатку помножимо обидві частини виразу (2.14) на , а потім проведемо інтегрування у замкненому контурі обох частин рівності. Якщо контур інтегрування лежить усередині зон збіжності нескінченного ряду (2.14), то операції підсумовування та інтегрування можна поміняти місцями, що дає:

.

Теорема Коші доводить: якщо контур інтегрування охоплює початок координат, то 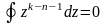для усіх , за винятком . Для інтеграл дорівнюватиме . При застосуванні даної властивості до останнього виразу, одержимо теорему про обернене Z - перетворення:

. (2.17)

Інтеграл у виразі (2.17) зручно обчислити за допомогою теореми про залишки: функція визначається сумою залишок підінтегральної функції у полюсах, розташованих на ділянці, яку охоплює контур інтегрування:

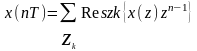, (2.18)

де - залишок функції відносно особливої точки .

Причому залишок у простому полюсі 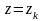дорівнює:

. (2.19)

Приклад 6. Нехай . Тут один простий полюс у точці і .

Зручний спосіб обчислення оберненого Z - перетворення полягає у розкладанні на прості дроби: .

У даному випадку, використовуючи властивості лінійності, знаходимо

. (2.20)

Приклад 7. Нехай .

Розкладемо на прості дроби . Згідно з формулою (2.20), відповідна решітчаста функція має вигляд .