
- •Цифрова обробка радіолокаційної інформації
- •Цифрова обробка радіолокаційної інформації
- •1. Призначення і принцип побудови системи цифрової обробки радіолокаційної інформації
- •2. Дискретні сигнали
- •2.1. Основні типи сигналів
- •2.2.5. Періодична послідовність
- •2.3. Спектри аналогових та дискретних сигналів
- •2.4. Дискретне перетворення Фур'є (дпф)
- •2.5. Згортка дискретних сигналів
- •Кругова (періодична) згортка дискретних сигналів
- •Лінійна (аперіодична) згортка дискретних сигналів
- •Пряме z - перетворення
- •2.6.2.Властивості z - перетворення
- •2.6.3. Обернене z - перетворення
- •Зв'язок між z - перетворенням і Фур'є - перетворенням
- •Дискретних систем
- •3.1. Алгоритми дискретних фільтрів
- •3.2. Розв'язання різницевих рівнянь
- •3.3. Передаточні функції
- •3.4. Форми реалізації дискретних фільтрів
- •3.5. Структурні схеми рекурсивних фільтрів
- •3.6. Структурні схеми нерекурсивних фільтрів
- •3.7. Часові й частотні характеристики лінійних дискретних фільтрів
- •3.8. Стійкість та реалізованість дискретних фільтрів
- •4. Цифровi фільтри
- •4.1. Зображення I кодування чисел, помилки квантування
- •4.1.1. Зображення чисел
- •4.1.2. Кодування чисел
- •Обернений код числа а (4.3) подається у вигляді
- •4.2. Помилки округлення й зрізання при квантуванні чисел та сигналів
- •4.3 Аналогово-цифровий перетворювач (ацп)
- •4.4 Цифро – аналоговий перетворювач (цап)
- •4.5. Апаратурна реалізація цифрових фільтрів
- •4.6. Фільтри з кінцевою імпульсною характеристикою й нескінченною імпульсною характеристикою
- •5. Принцип побудови системи збору й обробки рлі
- •5.1. Основні етапи й операції цифрової обробки рлі
- •5.2. Математичне формулювання задач обробки рлі
- •5.2.1. Загальне формулювання задач обробки
- •5.2.2. Задача виявлення
- •5.2.3. Задача оцінки параметрів
- •5.3. Дискретизація й квантування радіолокаційних сигналів
- •5.4. Статистичні характеристики квантованих сигналів
- •Закінчення
- •Література
4.6. Фільтри з кінцевою імпульсною характеристикою й нескінченною імпульсною характеристикою
Фільтром
з кінцевою імпульсною характеристикою
(КІХ
– фільтром)
називається фільтр, у якого імпульсна
характеристика являє собою кінцевий
дискретний сигнал (
-точечний
дискретний сигнал), тобто може приймати
відмінні від нуля значення тільки при

Фільтром
з нескінченною імпульсною характеристикою
(НІХ
– фільтром)
називають фільтр, у якого імпульсна
характеристика може приймати відмінні
від нуля значення на нескінченній
множині значень

Приклад
8.
Для нерекурсивного фільтра з передаточною
функцією
 в силу того, що
в силу того, що
 ,
можна обчислити імпульсну характеристику
таким чином:
,
можна обчислити імпульсну характеристику
таким чином:
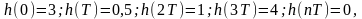 при
при
 .
Очевидно , що це КІХ – фільтр.
.
Очевидно , що це КІХ – фільтр.
Приклад
9.
Для рекурсивного фільтра з передаточною
функцією
 імпульсна характеристика визначається
таким чином:
імпульсна характеристика визначається
таким чином:
 .
Очевидно, що це НІХ – фільтр.
.
Очевидно, що це НІХ – фільтр.
Приклад
10.
Для рекурсивного фільтра з передаточною
функцією
 імпульсна характеристика визначається
таким чином:
імпульсна характеристика визначається
таким чином:
 ;
;
 при
при
 .
.
Очевидно, що це КІХ – фільтр.
Нерекурсивний фільтр завжди є КІХ - фільтром, у той же час рекурсивний фільтр може бути як НІХ - фільтром, та і КІХ - фільтром. Оскільки основні особливості проектування й застосування фільтрів пов’язані з видом імпульсної характеристики, а не з наявністю або відсутністю зворотного зв’язку, замість термінів “нерекурсивний” і “рекурсивний ” фільтр будемо використовувати терміни “КІХ - фільтр” і “НІХ - фільтр”.
4.6.1. КІХ – фільтри
Розглянемо ряд типових вимог до характеристик фільтра, сформульованих у вигляді окремих задач.
Перед
усім зазначимо, що частіше використовуються
нерекурсивні фільтри з достатньо
лінійною ФЧХ. У кожних задачах, що
розглядаються, під обчисленням фільтра
розуміють розв’язання апроксимованої
задачі – визначення за заданими вимогами
коефіцієнтів передаточної функції
фільтра. При нормуванні частоти
припускається, що
 і
і
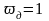 .
.
Задача
1.
Фільтр повинен мати достатньо лінійну
ФЧХ, а АЧХ фільтра
 має задовольняти заданим вимогам за
умови мінімуму величини
має задовольняти заданим вимогам за
умови мінімуму величини
 .
(4.14)
.
(4.14)
Вимога
 означає, що фільтр пропускає без
заглушення постійну складову (нульову
частоту), і отже, з малим заглушенням
близькі до нульової частоти низькі
частоти. Умова (4.14) відповідає максимальному
заглушенню стаціонарного шуму, що
надходить до фільтра.
означає, що фільтр пропускає без
заглушення постійну складову (нульову
частоту), і отже, з малим заглушенням
близькі до нульової частоти низькі
частоти. Умова (4.14) відповідає максимальному
заглушенню стаціонарного шуму, що
надходить до фільтра.
Задача 2. Фільтр повинен мати достатньо лінійну ФЧХ. АЧХ фільтра має задовольняти вимоги
 (4.15)
(4.15)
де
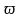 - нормована частота
- нормована частота

 -
задані функції. Критерій (4.15) називають
рівномірним критерієм апроксимації.
Як правило, цей критерій використовується
при проектуванні вибірних фільтрів і
фільтрів - коректорів.
-
задані функції. Критерій (4.15) називають
рівномірним критерієм апроксимації.
Як правило, цей критерій використовується
при проектуванні вибірних фільтрів і
фільтрів - коректорів.
Приклад 11. Нехай вимоги до АЧХ фільтра задаються у такій формі (рис. 4.8):
 .
(4.16)
.
(4.16)
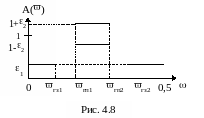
Умови (4.16) визначають вимоги щодо АЧХ смугового фільтра відповідно до критерію (4.15), причому
А*(
)=-
 і e(
)=
і e(
)= .
.
Задача
3.
Потужність власних шумів фільтра має
дорівнювати нулю. До ФЧХ фільтра не
ставлять яких-небудь вимог, а АЧХ фільтра
 має
має
задовольняти умову
 ,
(4.17)
,
(4.17)
де
 і
і
 – задані функції;
– задані функції;
e1 - константа.
Критерій (4.17) називають середньоквадратичним критерієм апроксимації. Як правило, цей критерій використовується при проектуванні фільтрів – подавлювачів шумів, а також при проектуванні вибірних фільтрів. Можна показати, що розв’язання задачі для КІХ - фільтра І-го порядку з передаточною функцією
 (4.18)
(4.18)
призводить до того, що
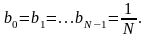 (4.19)
(4.19)
КІХ - фільтри з передаточною функцією (4.18) і коефіцієнтом (4.19) називаються однорідними фільтрами.
Існує три форми реалізації однорідного фільтра: нерекурсивна (рис.4.9), якій відповідають передаточна функція
 (4.20)
(4.20)
і різницеве рівняння
 (4.21)
(4.21)
і рекурсивна форма (рис.4.10), якій відповідають передаточна функція
 (4.22)
(4.22)
і різницеве рівняння
 (4.23)
(4.23)

Треба зазначити, що однорідні фільтри не містять перемножувачів, що дуже важливо при визначенні помилок квантування й збільшенні швидкодії.
На практиці часто використовується послідовне з’єднання однорідних фільтрів. Це дозволяє реалізувати частотні характеристики з кращими показниками в смузі пропускання й у смузі затримки. Так, послідовне з’єднання двох однорідних фільтрів однакового порядку призводить до тріангуляційного фільтра, що має значно більше заглушення у смузі затримки.
Послідовне з'єднання двох або більше однорідних фільтрів різних порядків дозволяє значно зменшити небажані підвищення АЧХ у смузі затримки шляхом відповідного вибору величини .
4.6.2. НІХ – фільтри
Задача проектування НІХ - фільтрів щодо заданих вимог до частотних характеристик є досить складною й багатоповерховою. Спочатку треба розв’язати апроксимаційну задачу, тобто визначити коефіцієнт передаточної функції фільтра щодо заданих вимог до частотної характеристики. Потім слід вибрати структуру фільтра й обчислити коефіцієнт вихідного сигналу, розрядність передаточної функції й внутрішніх кодів фільтра.
На
етапі розв’язання апроксимаційної
задачі визначають передаточну функцію
фільтра, яка б відтворювала задану АЧХ
з необхідною точністю. Звідси виходить,
що для розв’язання апроксимаційної
задачі як початкові дані мають задаватися
допуски max значення нерівномірності
АЧХ у смузі пропускання ( )
та max
відхилення АЧХ від нуля у смузі затримки
(
)
та max
відхилення АЧХ від нуля у смузі затримки
(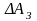 ).
).
При визначенні передаточних функцій НІХ-фільтрів використовуються такі методи:
- метод перетворення аналогових фільтрів у цифрові;
- прямий метод обчислення НІХ-фільтрів;
- метод, що використовує алгоритми оптимізації.
Для
обчислення вибірних НІХ-фільтрів зі
стандартними характеристиками (ФНЧ,
ФВЧ, СФ, РФ) найбільш простим і широко
використовуваним є метод білінійного
перетворення. За допомогою цього методу
передаточна функція
 аналогового фільтра - прототипу
перетворюється у передаточну функцію
цифрового НІХ-фільтра.
аналогового фільтра - прототипу
перетворюється у передаточну функцію
цифрового НІХ-фільтра.
Для цього можуть використовуватися широко відомі аналогові фільтри:
- фільтри Баттерворта (фільтри типу В);
- фільтри Чебишева (фільтр типу Т);
- інверсні фільтри Чебишева (фільтр типу С).
У ряді довідників щодо обчислення цих фільтрів подаються коефіцієнти передаточних функцій [7].
Білінійне
перетворення являє собою конформне
відображення точок
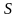 -
площини у точки
-
площини й використовує заміну змінної
вигляду
-
площини у точки
-
площини й використовує заміну змінної
вигляду
 (4.24)
(4.24)
де γ – постійний множник, значення якого не змінює форми перетворення.
Характер цього перетворення краще зрозуміти, якщо звернутися до (рис.4.11), де показано, яким чином - площина відображається у - площину. Видно, що:
-
вся вісь
 із
-
площини
відображується в одиночне коло на
-
площині;
із
-
площини
відображується в одиночне коло на
-
площині;
- ліва напівплощина відображається в одиночне коло;
- права напівплощина - в зону, що розташована поза одиночним колом на - площині.

Ці властивості легко доказати, якщо із формули (4.24) знайти вираз для :
 .
(4.25)
.
(4.25)
При

 .
(4.26)
.
(4.26)
Звідси
видно, що
 .
При
.
При
 і при
і при
 в інтервалі
в інтервалі
 змінюється від 0 до p.
Якщо підставити у формулу (4.25)
змінюється від 0 до p.
Якщо підставити у формулу (4.25)
 ,
отримаємо
,
отримаємо
 .
(4.27)
.
(4.27)
При
 (для лівої напівплощини)
(для лівої напівплощини)
 ,
тобто точки розміщуються у середині
одиночного кола.
,
тобто точки розміщуються у середині
одиночного кола.
Дуже важливими є дві обставини:
- по-перше, оскільки усі полюси стійкого аналогового фільтра розташовані у лівій половині - площини, він при перетворенні у ЦФ буде давати стійкий фільтр;
-
по-друге,
уявна вісь
- площини
відображається на одиночне коло
- площини,
тому усі
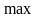 i
i
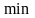 АЧХ (
АЧХ ( )
аналогового фільтра зберігаються й в
АЧХ (
)
аналогового фільтра зберігаються й в
АЧХ ( )
цифрового фільтра. Зберігається також
і нерівномірність АЧХ для відповідних
діапазонів частот.
)
цифрового фільтра. Зберігається також
і нерівномірність АЧХ для відповідних
діапазонів частот.
