
- •Для студентів для студентів спеціальності 6.040200
- •1. Взаємозв'язок фундаментального і прикладного соціологічного знання.
- •2. Предмет і функції прикладних соціологічних досліджень.
- •3. Місце соціологічної інформації в системі державного управління та в соціальній сфері.
- •1. Поняття методології, методу, технології та техніки соціологічних досліджень
- •2. Підстава для вибору методів збору й аналізу інформації в соціологічному дослідженні.
- •2. Поняття надійності.
- •3. Поняття валідності
- •4. Вимірювання та забезпечення надійності соціологічної інформації
- •5. Вимірювання точності (стійкості) соціологічної інформації
- •6. Вимірювання правильності соціологічної інформації
- •1. Проблема, об'єкт і предмет дослідження
- •2. Визначення мети й завдань дослідження
- •3. Уточнення й інтерпретація основних понять
- •4. Формулювання робочих гіпотез
- •5. Принциповий (стратегічний) план дослідження
- •6. Програмні вимоги до вибірки.
- •7. Загальні вимоги до програми
- •Суть вибіркового методу і його роль у соціології.
- •Обчислення помилки репрезентативності для властиво випадкової вибірки.
- •Плюси й мінуси властиво випадкової вибірки.
- •Стихійна вибірка.
- •Спрямований відбір.
- •Метод типових одиниць.
- •Цільова вибірка.
- •Квотний відбір.
- •Лекція 7. Метод опитування в соціологічних дослідженнях
- •1. Пізнавальні можливості методу опитування
- •2. Питання як інструмент одержання емпіричних даних
- •Лекція 8. Анкета. Проблема формулювання питань
- •Тема 10. Статистичний аналіз результатів прикладного соціологічного дослідження
- •Лекція 10. Особливості якісної методології в соціології
- •Из чого складається якісне дослідження?
- •Почому дослідники звертаються до якісних методів?
- •Які навички необхідні исследователю-каче-ственнику?
- •Чи можна сполучати якісний і кількісний методи?
- •Хто проводить якісні дослідження?
- •Які різновиди якісних методів?
- •Предмет дослідження: соціальні ролі і їхнє виконання
- •Способи пізнання індивідуального
- •Ідеологія дослідження - гуманістичний підхід
- •Рівень аналізу: мікропроцеси
- •Мова дослідження
- •Респондент як джерело достовірного знання
- •Методика й техніка проведення вільного інтерв'ю
- •Обробка матеріалів інтерв'ю
- •Література
- •Лекція Метод фокус-груп у соціологічному дослідженні
- •1.1. Природа фокусированного інтерв'ю
- •Використання фокусованих інтерв'ю
- •Критерії ефективності фокусованого інтерв'ю
- •Лекція Аналіз документів у соціологічних дослідженнях
Тема 10. Статистичний аналіз результатів прикладного соціологічного дослідження
(матеріали до лекції)
Основні функції статистичних методів в емпіричних соціологічних дослідженнях:
1) дескриптивна - опис соціальних об'єктів у кількісній формі
2) перевірка та уточнення гіпотез дослідження
3) одержання нових знань у формі соціально-статистичних фактів
4) прогнозування розвитку соціальних процесів.
Емпіричні (або конкретні) соціологічні дослідження мають ту особливість у порівнянні з дослідженнями переважливо теоретичного характеру, що при їх проведенні планується збирання та аналіз досить значної кількості первинної інформації. Первинну інформацію дослідник одержує за допомогою різних методів збирання інформації - інтерв'ю, анкетного опитування, спостереження, тощо.
Схематична (дуже спрощена) загальна послідовність етапів емпіричного соціологічного дослідження:
1. обрання тими дослідження
2. висунення низки дослідницьких питань стосовно обраної тими ("про що мі бажаємо дізнатися стосовно обраної тими?"). Питання можуть бути спрямовані або на опис ситуації (хто? що? скільки?) або на пояснення ситуації (чому?)
3. висунення дослідницьких гіпотез, як можливих варіантів відповіді на поставлені питання. Статистичний аналіз тільки може підтримати ("підтвердити") або не підтримати ("не підтвердити") висунуті гіпотези. Гіпотези повинні бути такими, щоб їх можна було емпірично перевірити (верифікувати або фальсифікувати). Гіпотези фіксують зв'язок між певними властивостями (характеристиками) об'єктів, що можуть змінюватися (між ознаками, між змінними).
4. збирання даних (вимірювання).
5. аналіз зібраних даних. Інтерпретація результатів аналізу. Перевірка, уточнення, зміна гіпотез.
Вимірюванням називається процедура, за допомогою якої об'єкти вимірювання, що розглядаються як носії певних співвідношень, відображаються в деяку математичну систему з відповідними відношеннями між елементами цієї системи. Сукупність властивостей об'єкту та чисел, що їм співставлені, називають шкалою.
Номінальні шкали При побудові такої шкали необхідно вміти встановлювати факт рівності або нерівності об'єктів з крапки зору ознаки, що розглядається. Така шкала розділяє всю множину об'єктів на класи (підмножини), що не перетинаються. Отримані числа можна порівнювати на рівність, алі не можна до них застосовувати арифметичні операції. До цих чисел можна застосовувати будь-які взаємно-однозначні перетворення.
Порядкові шкали. Шкала такого типу може бути побудована в тому випадку, коли між об'єктами (за даною ознакою) може бути встановлена не тільки рівність, алі й відношення послідовності (порядку). До кодів пунктів порядкової шкали можна застосовувати бу-яку монотонне перетворення.
Інтервальні шкали. В основі - емпірична
процедура, що дозволяє визначити відстань
між двома об'єктами. Є одиниця вимірювання.
Числові коди обирають таким чином, щоб
рівність інтервалів чисел відповідала
рівності інтервалів значень. Нуль
обирається довільно. До кодів пунктів
шкали можна застосовувати додатні
лінійні перетворення:
![]() (де
(де
![]() )
)
Шкали відношень встановлюється не
тільки рівність відношень між парами
об'єктів за певною ознакою, алі один і
тієї самий об'єкт відображається в 0.
Числа мають властивість рівності
відношень, тобто задовольняють всім
арифметичним аксіомам. Можна застосовувати
перетворення подібності
![]() (
)
(
)
У соціології різниця між інтервальними шкалами та шкалами відношень часто не важлива, тому говорять три типи шкали: номінальні, порядкові, метричні.
Дискретні змінні приймають значення з певного фіксованого переліку можливих значень. Неперервні змінні приймають значення із певного інтервалу можливих значень.
Дихотомічні змінні приймають лише
два можливих значення, які яки правило,
кодують числами 0 та 1. Дихотомічні змінні
можна розглядати як такі, що виділяють
певний клас об’єктів. Бу-якові номінальну
змінну з
![]() категоріями можна представити як серію
з
категоріями можна представити як серію
з
![]() дихотомічних змінних.
дихотомічних змінних.
Відповідно їх ролі в гіпотезі змінні поділяються на залежні та незалежні. Залежні - ті, характер змін (поведінку) яких мі намагаємося пояснити. Незалежні - ті, що пояснюють залежні (поведінка яких пояснює поведінку залежних, ті від яких залежати залежні змінні). До певної міри спрощуючи можна сказати, що незалежні змінні виступають як заподій, а залежні - як наслідки (у межах даної гіпотези). Як правило, у кожній гіпотезі одна незалежна змінна й одна або декілька незалежних. Яка змінна є залежною а яка незалежною - залежить від задачі, від гіпотези.
Концептуальна змінна (концепт) - є уявною конструкцією досить високого рівня абстракції. У термінах таких концептів зручно спілкуватися фахівцям та ставити задачі. Відштовхуючись від концептів визначаємо операціональні змінні (індикатори) - ті, що визначають конкретні дії (операції), які потрібно виконати для того, щоб визначити наявність або інтенсивність концептуальної ознаки. Стосовно індикатора відомо як виміряти цю змінну - задати питання, поставити людей у ситуацію і спостерігати тощо. Для деяких концептуальних змінних досить одного індикатора (пряме безпосереднє питання), алі більш часто концептуальна змінна операціоналізується декількома індикаторами, які потім "комбінуються" у нову змінну (конструкт), яка і вимірює концепт.
Надійність та валідність інструменту вимірювання. Надійність вимірювання показника – узгодженість результатів отриманих при повторному застосуванні тієї ж процедури вимірювання для оцінювання того ж показника на різних (алі репрезентативних для даного показника) вибірках. Валідність – міра відсутності в інформації теоретичних помилок (не зв'язаних з невірністю теоретичних припущень, невідповідністю числової моделі емпіричній системі, що вивчається, тощо).
Два підходи до аналізу даних - розвідувальний (пошуковий. експлораторний) та підтверджуючий (підтримуючий, конфірматорний).
Аналіз однієї змінної. Одновимірна таблиця - структура таблиці, частота, частка, відсоток, відсутні відповіді, відсоток по відношенню до загальної кількості об'єктів та по відношенню до кількості відповідей.
Міри центральної тенденції.
Для
даних, виміряних у метричних шкалах, у
якості міри центральної тенденції дуже
часто застосовується середнє
арифметичне:
![]()
Медіана Me -- значення ознаки, що припадає на центральний (середній) елемент впорядкованого ряду значень. Таким чином в однієї половини об'єктів значення ознаки менше ніж Me, а в другої половини -і більше. Медіана обчислюється для метричних та порядкових шкал.
Мода Мо -- значення ознаки, що найбільш часто зустрічається в даній сукупності об'єктів (тобто варіант з найбільшою частотою). Мода може обчислюватися також і для номінальних ознак.
Міри варіації -- це показники того, наскільки коливаються (змінюються, варіюють) значення певної ознаки в об'єктів сукупності.
Варіаційний
розмах
![]()
Дисперсія
![]() .
Розмірність дисперсії - квадрат
розмірності ознаки.
.
Розмірність дисперсії - квадрат
розмірності ознаки.
Середнє квадратичне (стандартне)
відхилення ![]() .
Має ту ж розмірність, що й ознака.
.
Має ту ж розмірність, що й ознака.
Коефіцієнт варіації
![]() ,
часто вимірюють у відсотках. Чим менше
коефіцієнт варіації - тім сукупність
більш однорідна. На практиці часто
сукупність називають однорідною за
даною ознакою тоді, коли відповідний
коефіцієнт варіації не перевищує
0.3-0.4.
,
часто вимірюють у відсотках. Чим менше
коефіцієнт варіації - тім сукупність
більш однорідна. На практиці часто
сукупність називають однорідною за
даною ознакою тоді, коли відповідний
коефіцієнт варіації не перевищує
0.3-0.4.
Як міру варіації використовують також показники, побудовані за допомогою квантилів. Наприклад, напівквартильне відхилення Q=Q3/4-Q1/4
Індекс якісної варіації
![]() дорівнює 1 якщо значення рівномірно
розподілені між категоріями
дорівнює 1 якщо значення рівномірно
розподілені між категоріями
Аналіз зв'язку між двома ознаками.
Структура двовимірної таблиці: клітинкові частоти, відсотки в рядку та в стовпчику, маргінальний рядок та маргінальний стовпчик
Якщо певному значенню однієї величини
X відповідає цілком визначене значення
іншої Y, те кажуть що між цими двома
величинами існує (має місце) функціональна
залежність. Якщо ж певному значенню
x1 однієї величини X відповідає
цілий комплекс значень
![]() іншої величини Y (ряд розподілу), причому
є певна залежність між зміною значення
X та зміною середнього відповідного
ряду розподілу Y, те кажуть що має місце
кореляційна (статистична) залежність
між величинами X та Y. Така статистична
залежність відображає тенденцію
збільшення (позитивна кореляція) чи
зменшення (негативна кореляція) однієї
величини при зростанні другої.
іншої величини Y (ряд розподілу), причому
є певна залежність між зміною значення
X та зміною середнього відповідного
ряду розподілу Y, те кажуть що має місце
кореляційна (статистична) залежність
між величинами X та Y. Така статистична
залежність відображає тенденцію
збільшення (позитивна кореляція) чи
зменшення (негативна кореляція) однієї
величини при зростанні другої.
Факт наявності зв'язку між двома
дискретними ознаками встановлюється
за допомогою так званого критерію
![]() .
Цей критерій базується на аналізі
частот, записаних у клітинках таблиці,
і дозволяє відповісти на питання, чи
можна висувати й аналізувати гіпотезу
про наявність зв'язку між двома ознаками
(зв'язок розуміється як відмінність від
статистичної незалежності двох ознак).
.
Цей критерій базується на аналізі
частот, записаних у клітинках таблиці,
і дозволяє відповісти на питання, чи
можна висувати й аналізувати гіпотезу
про наявність зв'язку між двома ознаками
(зв'язок розуміється як відмінність від
статистичної незалежності двох ознак).
Якщо
зв'язку немає, те в клітинці (і,j) має бути
![]() елементів.
елементів.
К.Пірсон запропонував таку міру відхилення емпіричної таблиці від теоретичної:
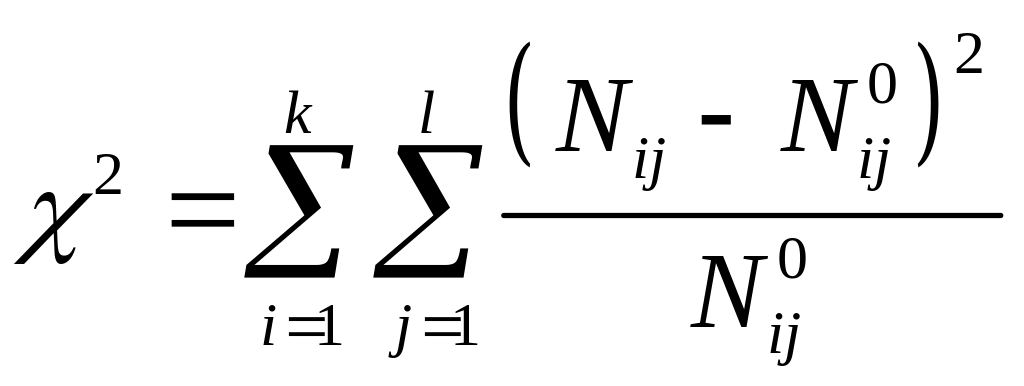
Чим більше тім більше відмінність. Оскільки мова йде про випадкові величини, наш висновок також винний носити імовірнісний характер: тобто висновок про розбіжність таблиць можна виносити лише з певною ймовірністю (наприклад, з ймовірністю p=0.99 або p=0.95 як це прийнято в соціальних дослідженнях), якові називають довірчою ймовірністю. Крім того кожна таблиця характеризується не тільки значенням , а й числом ступенів свободи f=(k-1)*(l-1).
Коефіцієнт може застосовуватися до даних, виміряних у будь-якій шкалі. Для того, щоб висновки на основі були надійні необхідно, щоб виконувалося принаймні дві умови:
кількість об'єктів винна бути не менше 100;
теоретичні частоти повинні бути не менше ніж 5 (деякі автори вважають 10); якщо це не так - треба перегрупувати таблицю, об'єднуючі рядки та стовпчики.
Чупров запропонував коефіцієнт, що базується на (2
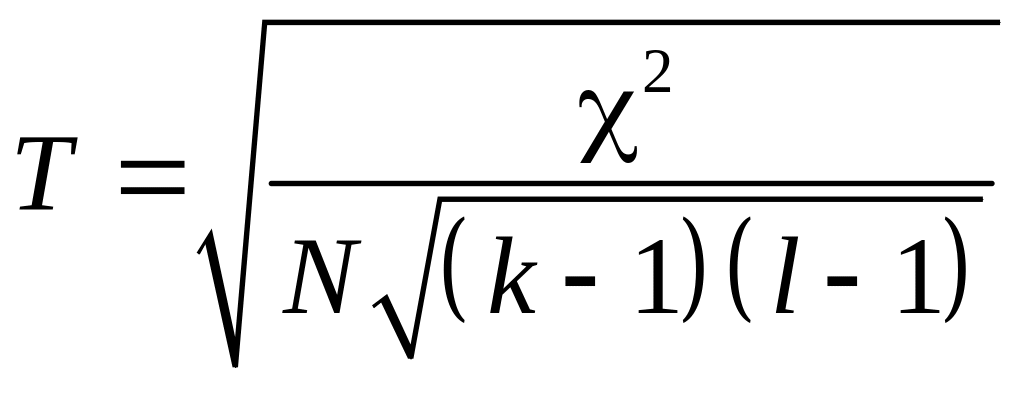
Коефіцієнт Чупрова досягає
максимального значення +1 у випадку
повного зв'язку алі тільки якщо
![]() (тобто таблиця є квадратною).
(тобто таблиця є квадратною).
Крамер запропонував замість
![]() використовувати
використовувати
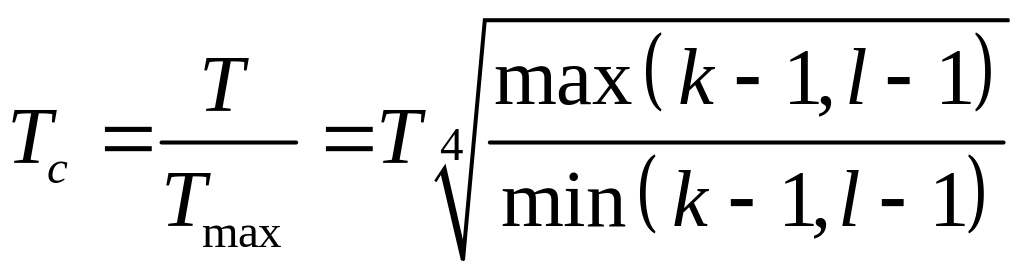 .
Легко бачити, що
.
Легко бачити, що
![]() ,
причому
,
причому
![]() при
.
при
.
![]() називають коефіцієнтом Крамера або
узагальненим коефіцієнтом Чупрова.
значно відрізняється від
для витягнутих таблиць.
називають коефіцієнтом Крамера або
узагальненим коефіцієнтом Чупрова.
значно відрізняється від
для витягнутих таблиць.
Кореляційний аналіз - сукупність методів, що використовуються для статистичного аналізу таких залежностей між змінними величинами, що мають характер кореляційних зв'язків.
Лінія, що проходити через умовні середні значення Y, називається лінією регресії.
В основі кореляційного зв'язку лежить уявлення про тип, форму та тісноту зв'язку, як властивості статистичної залежності.
Тіснота (щільність) зв'язку - характеристика ступеня взаємозалежності ознак. Зв'язок вважається більш тісним (більш щільним) якщо шкірному значенню однієї ознаки (фактора) відповідають близько розташовані одне від одного (щільно розташовані біля свого середнього) значення другої ознаки (результуючої ознаки). Найбільша щільність - у функціонального зв'язку.
За формою кореляційні зв'язки поділяються на лінійні та нелінійні. Лінійний - такий зв'язок, при якому збільшення значення фактора на 1 призводить до збільшення (зменшення) результуючої ознаки в середньому на одну й ту саму величину. Нелінійний зв'язок описує таку залежність, коли крапки з координатами x та y групуються навколо деякої кривої лінії так, що певному збільшенню фактора відповідає нерівномірне збільшення (або зменшення) результуючої ознаки.
У залежності від той, як розміщена на площині лінія регресії кореляційні зв'язки поділяються на два типи - прямий та зворотній. Прямий зв'язок - збільшення (зменшення) факторові веде до збільшення (зменшення) результуючої ознаки. Зворотній - навпаки
Коефіцієнт кореляції Пірсона r побудований виходячи з принципу сумісної варіації. Коефіцієнт r є мірою тісноти зв'язку двох ознак у припущенні що між цими двома ознаками існує лінійний кореляційний зв'язок. Обчислюється за формулою
![]()
Коефіцієнт r симетричний та змінюється від -1 до +1.
Кореляційне
відношення
![]() є відношення середнього квадратичного
відхилення умовних середніх
є відношення середнього квадратичного
відхилення умовних середніх
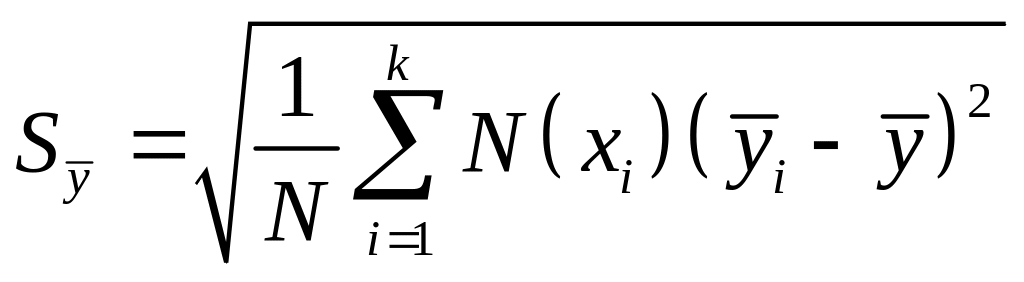
до повного середнього квадратичного
відхилення
![]() :
:
![]()
змінюється від 0 до +1.
1. ![]() якщо X та Y незалежні, алі навпаки невірно
якщо X та Y незалежні, алі навпаки невірно
2. ![]()
3. ![]() т. і т.т.коли є строга функціональна
залежність Y від X.
т. і т.т.коли є строга функціональна
залежність Y від X.
4. ![]() т. і т.т.коли кореляційний зв'язок має
лінійну форму, алі функціональної
залежності між Y та X немає
т. і т.т.коли кореляційний зв'язок має
лінійну форму, алі функціональної
залежності між Y та X немає
5. ![]() - є функціональна алі нелінійна залежність
між Y та X
- є функціональна алі нелінійна залежність
між Y та X
6. ![]() - немає функціональної залежності,
кореляційний зв'язок має нелінійну
форму
- немає функціональної залежності,
кореляційний зв'язок має нелінійну
форму
Досить часто показник
![]() розглядають як міру нелінійності
зв'язку.
розглядають як міру нелінійності
зв'язку.
Коефіцієнт рангової кореляції Спірмена побудований на принципі коваріації (сумісної варіації, зміни ) рангів (не значень а рангів).
Коефіцієнт рангової кореляції Кендела інтерпретується як різниця ймовірностей співпадання та неспівпадання порядку рангів за двома ознаками для парі навмання обраних об’єктів.
Статистичний висновок - деяке твердження про параметри генеральної сукупності (тобто числові характеристики, що описують генеральну сукупність) на основі статистик (тобто аналогічних характеристик, алі для вибірки). Носять індуктивний характер (від специфічного до загального). Такі твердження носять імовірнісний характер та розділяються на три види: точкові оцінки, інтервальні оцінки, перевірки статистичних гіпотез.
Точкове оцінювання: пошук показника, найбільш близького за значенням до параметра, що оцінюється.
Інтервальне оцінювання: пошук інтервалу, у якому з великою ймовірністю знаходиться значення параметра.
Перевірка статистичних гіпотез: формування деякого твердження про параметр (гіпотеза), оцінка результатів вибіркового дослідження гіпотези, рішення про прийняття або відхилення гіпотези
Точкове оцінювання. Властивості точкових оцінок:
Незсуненість
(ріс. - несмещенность)
- середнє вибіркового розподілу оцінки
дорівнює величині параметра. Середне
арифметичне - незсунена оцінка середнього.
Дисперсія - зсунена оцінка,
![]() (при
(при
![]() цією поправкою на зсув можна знехтувати).
цією поправкою на зсув можна знехтувати).
Обгрунтованість (ріс. - заможність) - при збільшенні обсягу оцінка прямує до значення параметра. Дисперсія - обгрунтована оцінка.
Ефективність - тім є вищою, чим меншою є дисперсія вибіркового розподілу статистики. Медіана - незсунута, обгрунтована оцінка середнього, алі її вибіркова дисперсія приблизно в 1.5 рази більше ніж у середнього арифметичного. Отже її ефективність менша ніж у середнього арифметичного.
Інтервальне оцінювання.
Будуємо інтервал (довірчий інтервал) на числовій осі, одна з точок якого ймовірно (з високою та гарантованою ймовірністю - довірчою ймовірністю) є значенням параметра.
Довірчий інтервал для середнього
Є
вибірка обсягом n з нескінченної
генеральної сукупності. За вибіркою
обчислені вибіркове середнє
![]() та вибіркове стандартне відхилення
та вибіркове стандартне відхилення
![]() .
Довірчий інтервал для довірчої ймовірності
для генерального середнього
.
Довірчий інтервал для довірчої ймовірності
для генерального середнього
![]() має
вигляд
має
вигляд
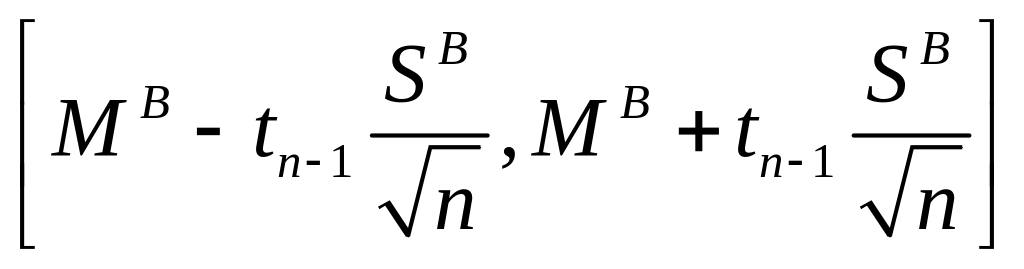
де
![]() - критичне значення розподілу Стьюдента
з (n-1) щаблями свободи для довірчої
ймовірності
.
- критичне значення розподілу Стьюдента
з (n-1) щаблями свободи для довірчої
ймовірності
.
Довірчий інтервал для коефіцієнту кореляції Пірсона
Є
вибірка обсягом n з нескінченної
генеральної сукупності. За вибіркою
обчислений вибірковий коефіцієнт
кореляції
![]() .
Довірчий інтервал для довірчої ймовірності
для генерального коефіцієнту кореляції
.
Довірчий інтервал для довірчої ймовірності
для генерального коефіцієнту кореляції
![]() має
вигляд
має
вигляд
![]() ,
,
![]() (обернене
перетворення Фішера)
(обернене
перетворення Фішера)
![]()
![]() ,
,
![]()
![]() (перетворення
Фішера)
(перетворення
Фішера)
Z - критичне значення розподілу N(0,1) для заданої довірчої ймовірності
Наукова гіпотеза - можливий розв'язок деякої проблеми (щось на зразок теореми). Статистична гіпотеза - деяке твердження відносно невідомих статистичних параметрів.
Загальна схема:
· Формулюємо нуль-гіпотезу i альтернативну гіпотезу.
· Висловлюємо припущення, необхідні для визначення вибіркового розподілу статистики, що оцінює параметр, відносно якого висловлюється гіпотеза. Вибірковий розподіл визначаємо для випадку, коли гіпотеза вірна.
· Визначаємо ризик прийняти невірне рішення про помилковість гіпотези (, рівень значущості, ймовірність помилки першого роду). Будуємо критичну область (ті значення, на основі яких приймається рішення про помилковість гіпотези).
· Робимо одну вибірку i виходячи з неї робимо висновок про справедливість гіпотези.
|
|
невірна |
відхиляємо |
помилка 1-го роду ( - рівень значущості |
Вірно 1-( |
приймаємо |
Вірно 1-( |
помилка 2-го роду ( - потужність критерію |
Якщо нуль-гіпотеза вірна, а мі її відхиляємо, те мі припускаємося помилки першого роду. Ймовірність такої помилки - (. Ймовірністю помилки першого роду можна керувати. Як правило, (=0.05, 0.01, 0.001.
Якщо нуль-гіпотеза невірна, а мі її приймаємо, те мі припускаємося помилки іншого роду. Ймовірність такої помилки - ( (потужність критерію). Керувати ймовірністю помилки іншого роду набагато складніше, ніж ймовірністю помилки першого роду. У соціології практично не використовуються помилки іншого роду. Нуль-гіпотези намагаються формулювати таким чином, щоб не було споживи визначати помилки іншого роду.
Значущість різниці часток (відсотків)
Є
дві генеральні сукупності, досить
великі, обсягом
![]() та
та
![]() .
З першої робимо випадкову вибірку
обсягом
.
З першої робимо випадкову вибірку
обсягом
![]() ,
з другої - обсягом
,
з другої - обсягом
![]() .
Нехай
.
Нехай
![]() - частка ознаки X у першій вибірці
- частка ознаки X у першій вибірці
![]() - частка ознаки X у другій вибірці
- частка ознаки X у другій вибірці
Гіпотеза
![]()
Нехай
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
тоді якщо гіпотеза
є вірною, те Z має розподіл N(0,1) ,
,
тоді якщо гіпотеза
є вірною, те Z має розподіл N(0,1) ,
де
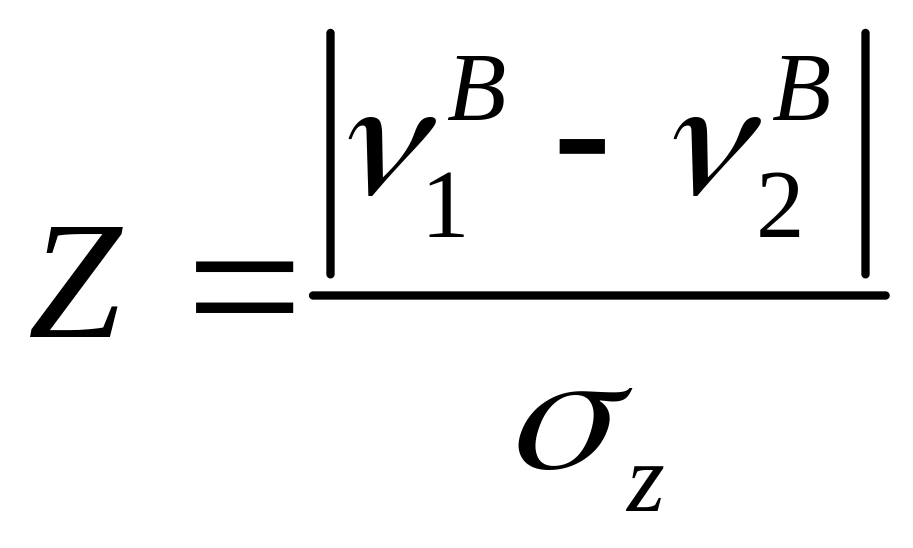 ,
,
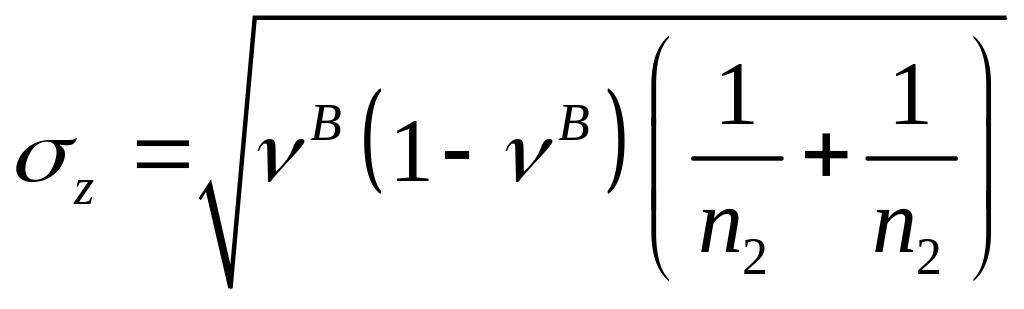 ,
,
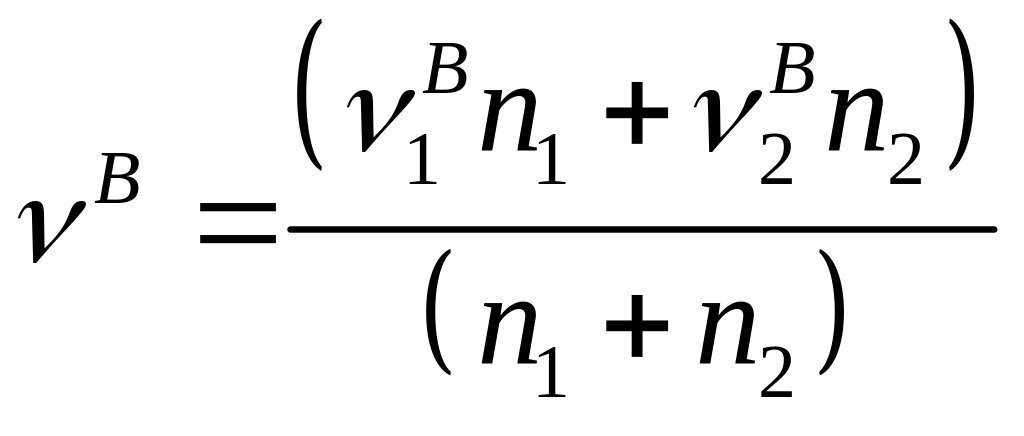
Таким чином, для перевірки гіпотези:
· обчислюємо Z
· визначаємо
для собі певний рівень значущості
(наприклад, 5%) і за таблицею знаходимо
відповідне критичне значення
![]() (для рівня значущості 5%,
=1.96)
(для рівня значущості 5%,
=1.96)
· якщо
![]() те
приймається, інакше - відхиляється
те
приймається, інакше - відхиляється
Форму статистичного зв'язку характеризує рівняння регресії. Одна з головних проблем регресійного аналізу - визначення форми зв'язку та її опис за допомогою рівняння регресії. Рівняння регресії наближено визначає залежність середнього значення однієї ознаки (відгук, результуюча ознака) від однієї або декількох ознак факторів:
![]()
Регресійний аналіз включає в собі: побудову рівняння регресії, його оцінювання та аналіз.
Вимоги до даних для застосування регресійного аналізу:
· всі змінні - кількісні (метрична шкала)
· сукупність об'єктів, що досліджується, винна бути якісно однорідною
· сукупність винна бути досить великою, щоб показники зв'язку були надійними та стійкими (кількість об'єктів винна бути в 6-8 разів більше кількості ознак)
· спостереження повинні бути статистично незалежні (тобто значення ознак в одного об'єкта ніяк не повинні залежати від значень в іншого); навести приклади залежних спостережень
· припущення:
шкірному значенню факторові (X) відповідає
нормальний (або майже нормальний)
розподіл результуючої ознаки (Y)
з однаковою дисперсією (![]() ).
).
Загальний вигляд рівняння множинної лінійної регресії
![]()
або (інше позначення)
![]()
Інтерпретація
- коефіцієнт
регресії:
![]() показує на скільки одиниць у середньому
змінюється результуюча ознака при зміні
відповідного фактора
показує на скільки одиниць у середньому
змінюється результуюча ознака при зміні
відповідного фактора
![]() на одну одиницю та незмінних (як правило,
середніх) значеннях інших факторів.
на одну одиницю та незмінних (як правило,
середніх) значеннях інших факторів.
Побудова рівняння множинної регресії здійснюється так саме за допомогою методу найменших квадратів. Для лінійного випадку (лінійна регресія)
![]() або
або
![]() .
.
Щоб знайти мінімум прирівнюємо до нуля часткові похідні
![]() ,
,
![]() ,
...,
,
...,
![]()
і отримуємо систему лінійних рівнянь
відносно
![]() -
(p+1) рівняння з (p+1) невідомими.
-
(p+1) рівняння з (p+1) невідомими.
Якщо виконати стандартизацію змінних
(перейти до стандартизованих координат
- середнє 0 дисперсія 1;
![]() )
те рівняння регресії "втратить"
вільний член і прийме вигляд
)
те рівняння регресії "втратить"
вільний член і прийме вигляд
![]()
де b та зв'язані
співвідношенням
![]() .
Оскільки в такому рівнянні регресії в
стандартних координатах всі змінні
безрозмірні, виміряні в співставимих
одиницях (власних середньоквадратичних
відхиленнях), те коефіцієнти (і демонструють
відносний вплив окремих факторів. Ці
коефіцієнти (на відміну від коефіцієнтів
рівняння регресії у звичайних координатах)
можна порівнювати між собою.
.
Оскільки в такому рівнянні регресії в
стандартних координатах всі змінні
безрозмірні, виміряні в співставимих
одиницях (власних середньоквадратичних
відхиленнях), те коефіцієнти (і демонструють
відносний вплив окремих факторів. Ці
коефіцієнти (на відміну від коефіцієнтів
рівняння регресії у звичайних координатах)
можна порівнювати між собою.
Питання оцінки якості рівняння регресії - наскільки добрі побудоване рівняння відображає поведінку наших даних (відповідає нашим даним).
Коефіцієнт множинної (сукупної) кореляції - оцінює сумарний вплив факторів на залежну ознаку.
![]()
Завжди
![]() для будь-яких j.
для будь-яких j.
![]() - коефіцієнт
детермінації,
що розкриває структуру дисперсії
залежної ознаки, тобто показує яка
частка (відсоток) дисперсії залежної
ознаки визначається факторами, що
входять до рівняння регресії.
- коефіцієнт
детермінації,
що розкриває структуру дисперсії
залежної ознаки, тобто показує яка
частка (відсоток) дисперсії залежної
ознаки визначається факторами, що
входять до рівняння регресії.
Загальна процедура побудови рівняння множинної регресії:
1. відбір ознак
2. аналіз однорідності за факторами (за кожним з факторів Ковар < 0.3-0.4)
3. аналіз кореляційної матриці й остаточний відбір факторів
4. побудова рівняння регресії у звичайних координатах; його оцінка та інтерпретація
5. побудова рівняння регресії в стандартизованих координатах; порівняння впливу факторів
6. у випадку, якщо рівняння погано відповідає даним (низький коефіцієнт детермінації) - змінити фактори й всі повторити.
Література
Робоча книга соціолога. - М.: Наука, 1983.- 512 с.
Дж.Гласс, Дж.Стэнли. Статистичні методи в педагогіці й психології. - М: Прогрес, 1976.- 495 с.
Паниотто В.И., Максименко В.С. Кількісні методи в соціологічних дослідженнях. - К.: Наукова думка, 1982.- 271 с.
Статистичні методи аналізу інформації в соціологічних дослідженнях / під ред. Осипова Г.В. - М.: Наука, 1979.- 319 с.
Соціологічний довідник / під ред. Воловича В. И. - К.: Политиздат України, 1990.- 382 з.
Енциклопедичний соціологічний словник / під ред. Осипова Г.В. - М: ИСПИ РАН, 1995.- 939 с.
Соціологія: короткий енциклопедичний словник / під ред. Воловича В.І.- К.: Український Центр духовної культури, 1998.- 736 с.
Сигел Э. Практична бізнес-статистика. - М.: Видавничий будинок "Вільямс", 2002 - 1056 с.
А.Бююль, П.Цефель SPSS: Мистецтво обробки інформації.- Спб.: ТОВ "Диасофтюп", 2001.- 608 с.
Малхотра Н.К. Маркетингові дослідження. - М.: Видавничий будинок "Вільямс", 2002 - 960 с.
