7. Вычисление дирекционных углов и румбов сторон замкнутого хода

Исходный дирекционный угол, например, сторон 1 – 2 хода (рис. 7.5.1.) получают в результате привязки этой стороны к пунктам геодезической опорной сети или определяют для нее истинный или магнитный азимут.

По известному дирекционному углу и по исправленным углам вычисляют дирекционные углы всех сторон замкнутого хода по формулам:

(7.5.1.)

Последняя строка равенств контрольная.

По дирекционным углам вычисляют румбы.

Рис. 7.5.1. Схема обработки замкнутого теодолитного хода

8. Угловая невязка разомкнутого теодолитного хода

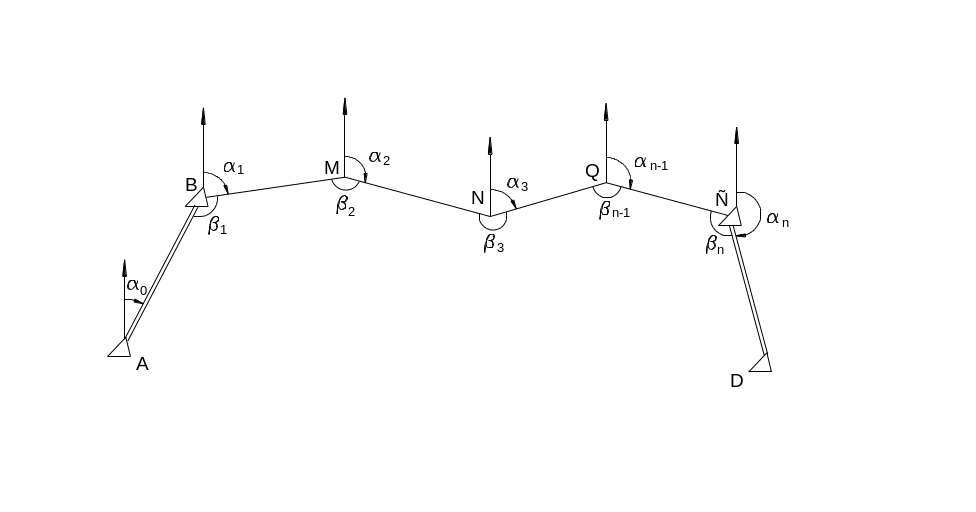
Рис. 7.6.1. Схема обработки разомкнутого теодолитного хода

Координаты исходных точек А, В и С, D опорной сети и дирекционные углы ₀ и _n известны. Угловая невязка разомкнутого хода (рис. 7.6.1.) вычисляется по формуле

(7.6.1.)

9. Вычисление дирекционных углов и румбов сторон разомкнутого теодолитного хода

Координаты исходных точек A, B и C, D опорной сети и дирекционные углы α₀ и α_n (рис. 7.6.1.) известны. Из рисунка следует

,

т. е. дирекционный угол каждой последующей линии равен дирекционному углу предыдущей линии плюс 180°, минус вправо по ходу лежащий угол.

10. Прямая и обратная геодезические задачи

При вычислительной обработке результатов измерений на местности, при проектировании инженерных сооружений и перенесении их в натуру возникает необходимость решить прямую и обратную геодезические задачи (рис. 7.7.1.).

Прямая геодезическая задача.

Рис. 7.7.1. Прямая и обратная геодезические задачи

Даны координаты x₁ и y₁ точки А начала линии АВ, ее горизонтальное проложение d и дирекционный угол . Требуется определить координаты x₂ и y₂ точки В конца этой линии. Из рисунка видно, что координаты

(7.7.1.)

Разности координат конечной и начальной точек линии АВ, т. е. x и y называются приращениями координат:

(7.7.2.)

При помощи румбов приращения координат вычисляются по формулам:

(7.7.3.)

Приращения координат имеют знаки, которые зависят от знака косинуса и синуса дирекционного угла или от названия румба линии:

Румбы	СВ	ЮВ	ЮЗ	СЗ
Приращения:
x	+	-	-	+
y	+	+	-	-

Вычисление приращений координат выполняют с помощью таблиц натуральных значений sin и cos или с помощью вычислительных машин.

Обратная геодезическая задача. Даны координаты x₁ и y₁ точки А начала линии АВ и координаты x₂, y₂ точки В конца этой линии. Требуется определить длину и дирекционный угол или румб этой линии. Из рисунка следует, что

(7.7.4.)

или

, (7.7.5.)

r определяют по таблицам натуральных значений тригонометрических функций или с помощью микрокалькулятора. Название румба определяют по знакам y и x. По румбу можно вычислить дирекционный угол .

Расстояние d вычисляется по формулам

(7.7.6.)

или

. (7.7.7.)