6.4.2. Давление пара растворителя

Уравнение Гиббса-Дюгема позволяет найти давление пара растворителя в зависимости от его концентрации, если известна зависимость давления пара растворенного вещества как функция температуры.

Выражая концентрацию в молярных долях и логарифмируя выражение (6.12), получим уравнение

,

дифференцирование которого дает по дает

или .

Отсюда, согласно уравнению :

и ,

где С – константа интегрирования и . Для определения С примем , тогда, очевидно, равно давлению пара чистого растворителя

. (6.15)

Это уравнение выражает закон Рауля, согласно которому давление пара растворителя над раствором меньше, чем давление пара чистого растворителя, и пропорционально молярной доле растворителя.

Исторически это закон был открыт эмпирическим путем на основании измерений давления пара различных органических растворителей над растворами. Рауль предложил для него следующую формулировку, равносильную уравнению (6.15): относительное понижение давления пара растворителя равно молярной доле растворенного вещества:

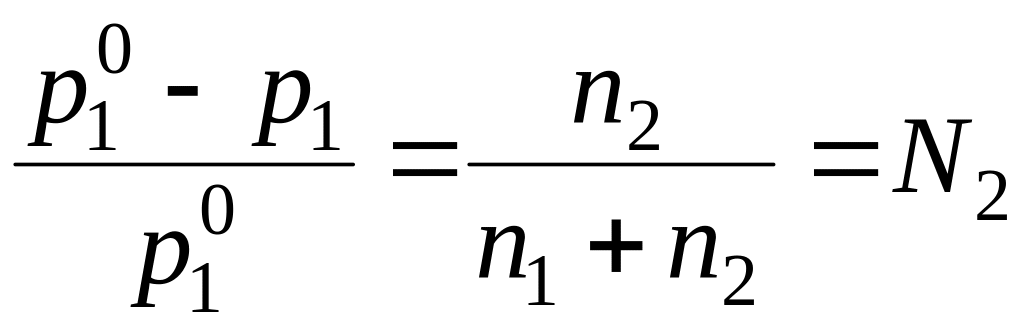. (6.16)

В отличие от закона Генри, который справедлив при любом способе выражения концентрации, закон Рауля требует, чтобы она выражалась в молярных долях. Оба закона справедливы для разбавленных растворов.

Из закона Рауля вытекают важные следствия, касающиеся температур кипения и замерзания разбавленных растворов нелетучих веществ.

6.4.3. Температура кипения и замерзания разбавленных растворов нелетучих веществ

Следствием понижения давления пара растворителя является то, что температура кипения раствора, т. е. температура при которой давление его пара становится равным атмосферному, должна быть выше, чем для чистого растворителя. Схематически это показано на рисунке 6.3, где и – соответственно температура кипения раствора и растворителя, и – повышение температуры кипения. При температуре кипения атм. Логарифмируя это уравнение и дифференцируя по температуре, получим

.

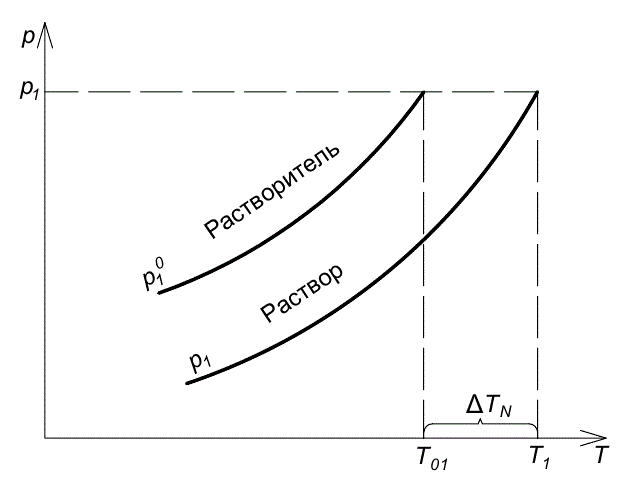
Рис. 6.3. Повышение температуры кипения раствора

Так как по уравнению Клапейрона – Клаузиуса , то , где – молярная теплота испарения растворителя из раствора.

Интегрирование в интервале между и дает

. (6.17)

Для разбавленных растворов N₂ << N₁, т. е. при разложении в ряд выражения можно ограничиться первым членом с точностью до 1%, если N₂ < 0,02. В случае разбавленных растворов и различаются незначительно и произведение может быть заменено , а величина не отличается заметно от теплоты испарения чистого растворителя. Таким образом, из уравнения (6.17) следует, что

.

Выразим концентрацию раствора через моляльность С_m. Пусть раствор содержит n молей растворенного вещества в 1000 г растворителя. В этом случае . Если молярная масса растворителя M₁, то . В разбавленном растворе можно пренебречь величиной С_m по сравнению с 1000/М₁, тогда . Отсюда

, (6.18)

где l – удельная теплота испарения растворителя; – постоянная величина – эбуллиоскопическая константа, которая характеризует свойства растворителя.

Из уравнения (6.18) следует, что повышение температуры кипения разбавленного раствора не зависит от природы растворенного вещества, а определяется только природой растворителя и моляльностью. Таким образом, величина К_э характеризует повышение температуры кипения раствора, содержащего 1 моль любого вещества в 1000 г растворителя. В действительности К_э может и не быть равной повышению температуры кипения моляльного раствора, так как при такой концентрации необязательно сохраняются свойства разбавленного раствора. Поэтому К_э обычно определяют экстраполяцией на нулевую концентрацию отношения . Уравнение (6.18) было подтверждено многочисленными опытными данными. Впоследствии будет показано, что оно неприменимо в такой простой форме к растворам электролитов.

В качестве примера вычислим величину К_э для воды ( =373 К, а l = 539 кал/г):

.

Из уравнения (6.18) следует, что измерения температур кипения растворов могут служить для определения молекулярной массы растворенного вещества (эбуллиоскопический метод). Если масса растворителя m₁, а растворенного вещества с молекулярной массой М₂ – m₂, то моляльность

, откуда .

Другим следствием понижения давления пара раствора нелетучим растворенным веществом является то, что температура замерзания раствора становится ниже, чем чистого растворителя. Температура замерзания чистого растворителя определяется условием равенства давления его пара над жидкой и твердой фазами. Если при замерзании раствора выделяется чистый растворитель, то давление пара над раствором также должно быть равно давлению растворителя в твердом состоянии. Как видно из рис. 6.4, это приводит к понижению температуры замерзания раствора.

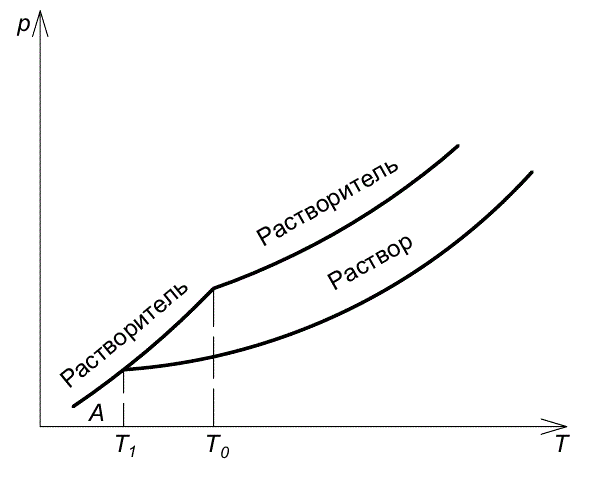
Рис. 6.4.Понижение температуры замерзания раствора

Используя такие же соображения, как при выводе уравнения (6.18), легко получить из уравнения выражение для понижения температуры кристаллизации (замерзания):

и (6.19)

где К_к – криоскопическая постоянная, т.е. понижение температуры замерзания моляльного раствора, определяемое уравнением

,

здесь r – удельная теплота плавления растворителя; – его температура плавления (замерзания).

Величина К_к зависит только от свойств растворителя. Поэтому понижение температуры замерзания разбавленных растворов в данном растворителе определяется только концентрацией растворенного вещества.

Применение уравнения (6.19) может быть показано на примере железа, теплота плавления которого составляет 62,74 кал/г, а температура плавления = 1812 К и К_к = 1,985·1812²/(1000·62,74) = 101,5 К.

Таким образом, если из расплава кристаллизуется чистое железо, то понижение температуры плавления в расчете на 1 моль растворенного вещества в 1000 г железа должно составлять 101,5 ºС. Это наблюдается с известным приближением для растворов серы и бора в железе (М (S) = 32 г/моль, М (B) = 10,82 г/моль).

В случае 1%-ного раствора серы в железе экспериментально найденное понижение температуры плавления раствора составляет 30º. Моляльность такого раствора С_m = 10:32 ≈ 0,31 и = 101,5·0,31 = 32 К.

В случае 1% раствора бора в железе температура плавления раствора понижается на 90 К, моляльность С_m = 10:10,82 = 0,92 и = 101,5·0,92 = 93,4 К.

Уравнение (6.19) также может быть использовано для определения молекулярной массы растворенного вещества (криоскопический метод):