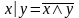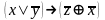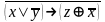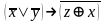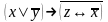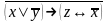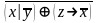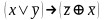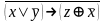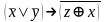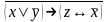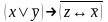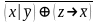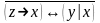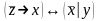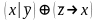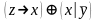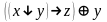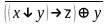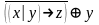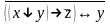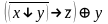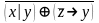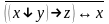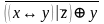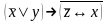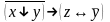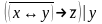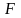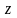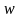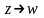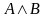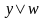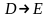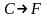- •Требования к оформлению контрольной работы
- •Тема 1: «Булевы функции. Таблицы истинности. Формулы. Разложение по переменным»
- •Варианты
- •Тема 2: «Полином Жегалкина. Метод неопределенных коэффициентов»
- •Тема 3: «Полнота систем булевых функций»
- •Тема 4: Минимизация булевых функций в классе днф
- •Донецьк-2013 г.
КОМПЬЮТЕРНАЯ ДИСКРЕТНАЯ МАТЕМАТИКА
Требования к оформлению контрольной работы
Работа выполняется на листах А4 в редакторе Word или от руки. Титульный лист набирается обязательно в редакторе Word. Образец титульного листа – в конце задания.
Номер варианта равен остатку от деления числа, образованного двумя последними цифрами в номере зачетки, на 20. Если остаток=0, то выбирается 20-й вариант.
Для каждого задания (их три) пишется тема и условие задания, затем приводится подробное решение с объяснениями и ответом.
Литература – в конце мет-ки.
Тема 1: «Булевы функции. Таблицы истинности. Формулы. Разложение по переменным»
|
y |
0 |
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
|
|
|
|
|
1 |
|
– дизъюнкция
| – штрих Шеффера |
|
0 |
0 |
1 |
1 |
1 |
1 |
|||
0 |
1 |
1 |
1 |
1 |
1 |
|||
1 |
0 |
0 |
0 |
1 |
1 |
|||
1 |
1 |
0 |
1 |
0 |
1 |
Теоретические сведения – в методичке.
Задание к теме 1.
Построить таблицу функции.
По таблице составить совершенные ДНФ и КНФ.
Построить совершенные ДНФ и КНФ по исходной формуле с помощью эквивалентных преобразований.
Найти разложение БФ в дизъюнктивную форму по переменным x, z. Проверить результат с помощью таблицы.
Упростить исходную формулу с помощью эквивалентных преобразований и проверить результат с помощью таблицы.
Варианты
Приоритет операций в данном задании:
скобки
отрицание
конъюнкция
дизъюнкция
остальные – слева направо с учетом скобок.
Тема 2: «Полином Жегалкина. Метод неопределенных коэффициентов»
Теоретические сведения.
Рассмотрим, как вычисляются коэффициенты полинома Жегалкина для функции 4-х аргументов на примере.
Пусть требуется представить полиномом Жегалкина следующую функцию:
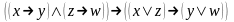 .
.
Сначала построим таблицу истинности функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
1 |
1 |
0 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
|
|
|
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Для функции 4-х переменных коэффициенты полинома Жегалкина вычисляются по формулам, приведенным справа.
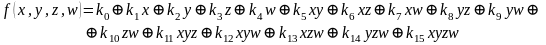
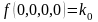 ,
,
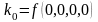 ,
,
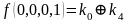 ,
, 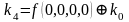 ,
,
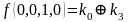 ,
, 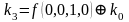 ,
,
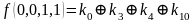 ,
, 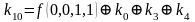 ,
,
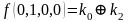 ,
, 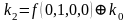 ,
,
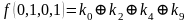 ,
, 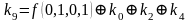 ,
,
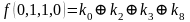 ,
, 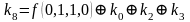 ,
,
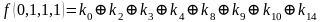 ,
,
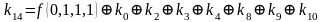 ,
,
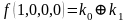 ,
, 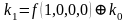 ,
,
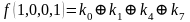 ,
, 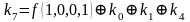 ,
,
 ,
, 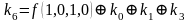 ,
,
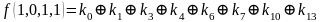 ,
,
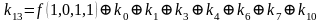 ,
,
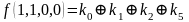 ,
, 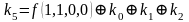 ,
,
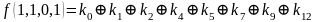 ,
,
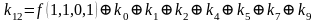 ,
,
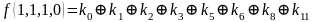 ,
,
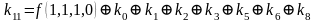 ,
,
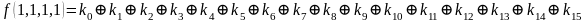
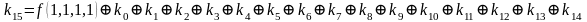
Пример. Найти полином Жегалкина для функции от двух переменных, заданной вектором значений:
f( x,y ) = ( 0, 1, 1, 0 ).
Составим таблицу истинности для данной функции:
x |
y |
f |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
0 |
1 |
1 |
1 |
0 |
Полином Жегалкина для функции двух переменных ищем в следующем виде:
f( x, y ) = k0 k1·x k2·y k12·xy (1)
Для определения коэффициентов полинома нужно подставить значения переменных и соответствующее значение функции в формулу (1), согласно таблице истинности.
Подставляя набор переменных (0,0) в (1) получаем:
0= f( 0, 0 ) = k0 k1·0 k2·0 k12·0·0 = k0 k0 = 0.
Аналогично для набора (0,1) получаем:
1= f( 0, 1 ) = 0 k1·0 k2·1 k12·0·1 = k2 k2 = 1.
Для набора (1,0) получаем:
1= f( 1, 0 ) = 0 k1·1 k2·0 k12·1·0 = k1 k1 = 1.
Для набора (1,1) получаем:
0= f( 1, 1 ) = 0 1·1 1·1 k12·1·1 = 1 1 k12 = 0 k12 = k12 k12 = 0.
Подставляя в (1) найденные значения коэффициентов, получаем искомый полином для данной функции: f( x, y ) = x y.
Задание к теме 2. Для функции из задания №1 постройте полином Жегалкина двумя способами:
а) методом неопределенных коэффициентов;
б) с помощью эквивалентных преобразований.
Сравнив оба результата, проверьте правильность построенного полинома.

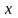
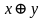
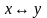
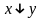
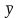
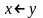
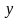
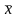
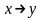
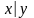
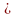 – конъюнкция
– конъюнкция – импликация
– импликация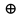 – сумма по модулю
2
– сумма по модулю
2 – стрелка Пирса
– стрелка Пирса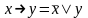
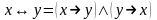
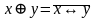
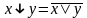 ,
,