0. 3.3 Визначення регресійної функції. Оцінка якості регресійної моделі

Для визначення типу регресійної функції проводиться аналіз емпіричних даних по наступних напрямках:

1. Визначення напрямку зв’язку.

2. Визначення зміни напрямку зв’язку досліджуваної сукупності (чи є залежність монотонною).

3. Визначення характеру змін: рівномірно прискорюваних або що вповільнюються (лінійного або нелінійного характеру).

Необхідні, для визначення типу функції, відомості одержують із емпіричного матеріалу. Висновок про напрямок і форму зв’язку (аналітичному вираженню) можна одержати шляхом паралельного порівняння рядів показників, а також із графічного аналізу.

У наступній таблиці наведені типи функцій, що використовуються найбільше часто для опису парних та багатофакторних залежностей.

У таблиці прийняті наступні позначення:

а₀ – довільний член регресії,

а₁ – коефіцієнт регресії.

Таблиця 3.2 – Типи регресійних функцій

Найменування	Функція	Випадок використання
Лінійна	,	X і Y зростають приблизно в арифметичній прогресії.
Гіперболічна	,	Зв’язок між X і Y зворотний.
Показова	,	Логарифми Х зростають приблизно в арифметичній прогресії.
Параболічна		X збільшується в арифметичній прогресії, а Y значно швидше.
Ступенева
Логістична		Відношення приростів логарифмів Х є постійною величиною.

З наведених форм зв’язку вибирають за формальними критеріями апроксимації одну. Для цього рекомендується використовувати один із двох критеріїв, що характеризують середню помилку апроксимації функції:

1. Показник середньої помилки апроксимації:

,

де: n – число значень досліджуваного показника,

- i–е значення досліджуваного показника,

- вирівняне по функції i–е значення досліджуваного показника.

2. Показник середньої квадратичної помилки:

,

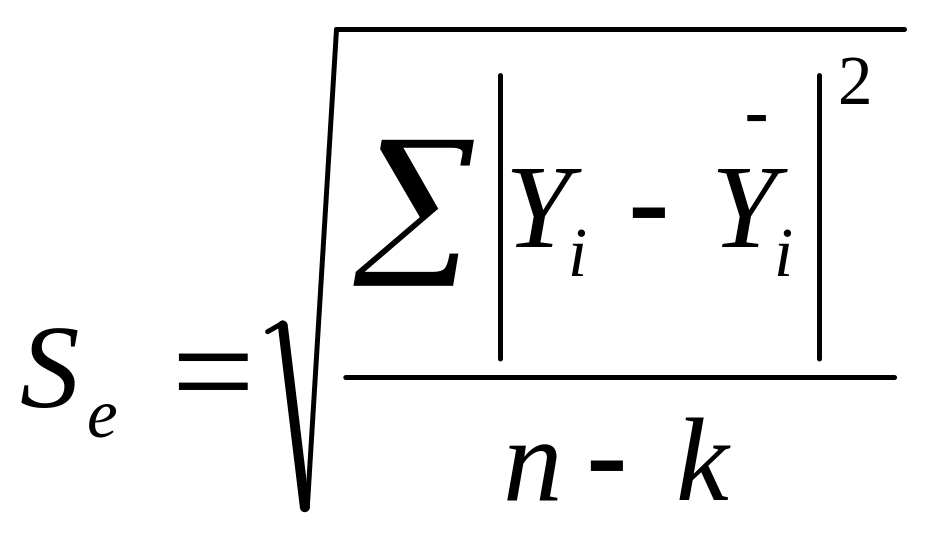де: k – число факторних ознак.

Застосування зазначених критеріїв є досить надійним способом відбору адекватних математичних моделей, при цьому значення помилки апроксимації не повинне перевищувати 12% - 15%.

Вірогідність побудованої регресійної моделі можна перевірити за допомогою коефіцієнта детермінації (R²):

, , (3.4)

де - значення параметра Y, розраховане відповідно до регресійної моделі.

Коефіцієнт детермінації показує якою мірою варіація результативного показника обумовлена впливом факторних показників.

Якщо , то лінія регресії точно відповідає всім спостереженням.

Коли можна стверджувати, що видимий зв’язок між X і Y є відсутній.

Якщо R² має нечітко виражене граничне значення (наприклад, 0.5), то в таких випадках зручно використовувати критерій Фішера або F-Тест.

При проведенні F-Тесту будемо вважати нульовою гіпотезою те, що значення R² отримане випадково й між величинами немає зв’язку.

Порядок перевірки моделі на адекватність за критерієм Фішера такий:

1. Розрахунок величини F-відносини:

(3.5)

2. Вибір користувачем рівня значимості =0,05 або =0,01.

3. По статистичних таблицях F-розподілу знаходимо граничне значення F_кр при v₁=( k-1) і v₂=( n-k) ступенях волі.

Якщо розраховане значення , то відкидається нульова гіпотеза з ризиком помилки не більше, ніж у випадків.

Потім провадитися оцінка значимості коефіцієнтів регресії за допомогою t-критерію Ст’юдента:

. (3.6)

Параметр моделі зізнається статистично значимим, якщо ,

де - рівень значимості критерію перевірки гіпотези про рівність нулю параметрів, що вимірюють зв’язок (задається користувачем),

- число ступенів волі, що характеризує число вільно елементів сукупності, що варіюють.

Після оцінки значимості всіх коефіцієнтів регресії з моделі виключається той фактор, коефіцієнт при якому є не значимим й має найменше значення критерію.

Таким чином, при виборі кращої регресійної моделі варто керуватися такими принципами:

1. Модель повинна бути адекватною за F-критерієм Фішера.

2. Коефіцієнти регресії повинні бути статистично значимі (задовольняти t-критерію Ст’юдента).

3. Обрана математична функція повинна мати мінімальну помилку апроксимації серед всіх розглянутих рівнянь регресії.

При цьому можливі наступні варіанти:

1. Побудована модель на основі перевірки за F-критерієм Фішера адекватна, і всі її коефіцієнти значимі. Така модель може бути використана для прийняття рішень і здійснення прогнозів.

2. Модель за F-критерієм Фішера адекватна, але частина коефіцієнтів регресії незначима. У цьому випадку модель придатна для прийняття рішень, але не повинна використовуватися для прогнозування. Використання моделі для прогнозування можливо після виключення факторів, коефіцієнти яких є незначимі.

3. Модель за F-критерієм Фішера адекватна, але всі коефіцієнти регресії є незначимі. Така модель повністю вважається неадекватною.

Параметри рівняння регресії розраховуються за методом найменших квадратів.

а_i- параметр, що показує на скільки одиниць свого виміру зміниться Y, якщо x_i збільшитися на одну одиницю свого виміру, за умови, що всі інші фактори, включені в модель, впливають на Y, але не варіюють, тобто зафіксовані на рівні свого середнього значення.

а₀ – параметр, що виражає сукупний вплив всіх неврахованих факторів, його внесок у значення результуючого показника не залежить від зміни факторів.

По параметрах рівняння можна оцінити частку кожного з факторів у зміні рівня результативного показника. Це може бути зроблено шляхом прямої оцінки за величиною коефіцієнтів регресії, а так само і за коефіцієнтом еластичності:

. (3.7)

Коефіцієнт еластичності показує, на скільки відсотків зміниться результативний показник при зміні факторного показника на один відсоток при фіксованому положенні інших факторів.

Чим більше величина коефіцієнта регресії, тим значніше вплив даного показника на результуючий. Особливе значення при цьому має знак перед коефіцієнтом регресії.

Знаки говорять про характер впливу на результативний показник. Якщо факторний показник має знак плюс, то зі збільшенням даного фактору результативний показник зростає; якщо факторний показник має знак мінус, то з його збільшенням результативний показник зменшується.