3. Правила комбинаторики

Правило суммы. Если некоторый выбор из совокупности можно сделать n различными способами, а другой выбор — m различными способами (отличными от предыдущих), то общее число способов, которыми можно осуществить какой-нибудь из этих выборов, равен сумме n+m.

Пример 8. Сколько всего различных двузначных и трехзначных чисел можно записать цифрами 7, 3, 1, 2?

Решение. Необходимо найти количество двузначных чисел, затем количество трехзначных чисел и сложить полученные результаты. Так как порядок расположения цифр в числе имеет значение, то есть числа 37 и 73 — это разные числа, то количество двузначных чисел равно числу размещений 4´3=12, а количество трехзначных чисел равно 4´3´2=24, пользуясь правилом суммы, можно найти общее число различных двузначных и трехзначных чисел 12+24=36.

Правило произведения. Если некоторый выбор из совокупности можно сделать n различными способами, а для каждого из этих способов некоторый второй выбор можно сделать m различными способами, тогда число способов для проведения последовательно двух этих выборов равно произведению n´m.

Пример 9. Клавиатура пианино состоит из 88 клавиш (нот). Сколько различных музыкальных фраз можно составить из 6 нот, если не допускать в одной фразе повторение одних и тех же нот.

Решение. В качестве первой ноты для музыкальной фразы можно взять любую из 88 нот, то есть для первой ноты имеем 88 возможностей. Так как повторения не допускаются, то для второй ноты имеем лишь 87 возможностей, для третьей ноты останется лишь 86 возможностей, рассуждая аналогично, получим, что число различных музыкальных фраз из 6 нот без повторения равно произведению 88´87´86´85´84´83=390 190 489 920.

4. Рекомендации для самостоятельной работы

1. Прочтите цели изучения темы, для того чтобы знать, что нужно научиться делать, чтобы усвоить изучаемый материал.

2. Изучите справочные материалы и примеры.

3. Составьте конспект изученного в рабочей тетради, для этого: выпишите определение комбинаторики; основные определения и формулы комбинаторики (заполняя следующую таблицу); приведите примеры «из жизни и личного опыта» для их иллюстрации.

Таблица 7

Операции	Перестановки	Размещения	Сочетания
Определение
Обозначение
Формула
Пример

4. Решите задания для самоконтроля 1-го уровня.

5. Задания для самостоятельной работы

1. Запишите правильно следующие математические термины и символьные математические записи:

а) факториал; б) сочетания; в) размещения; г) перестановки; д) n! ; е) C_n^k ; ж) А_n^k ; з) Р_n.

2. Соотнесите термины комбинаторики и их обозначения. Поставьте знак «+» в соответствующей клетке таблицы.

	перестановки	сочетания	размещения
Pn

3. Заполните пропуски так, чтобы получилось верное утверждение:

а) … из n элементов по k (0 ≤ k ≤ n) элементов называется упорядоченное подмножество, содержащее k различных элементов данного множества;

б) … из n элементов по k (0 ≤ k ≤ n) элементов называется любое подмножество, содержащее k различных элементов данного множества;

в) различные … из n элементов отличаются друг от друга только порядком следования элементов.

4. Укажите, как правильно с помощью символов записать выражение «не более 4-х». Варианты ответов:

а) < 4 (меньше 4-х);

б)  4 (больше или равно 4-м);

в)  4 (меньше или равно 4-м).

5. Соотнесите обозначения (перестановки, размещения, сочетания) и формулы для вычисления их числа. Поставьте знак «+» в соответствующей клетке таблицы.

	n!	___n!___ (n–k)!k!	___n!___ (n–k)!
Pn=
=

6. Вычислите: а) 0!=…; б) 2!=…; в) 5!=…; г) P5–P4=…

7. Укажите, какие значения может принимать параметр k в формуле , если n=4.

Варианты ответов: а) 1; 2; 3; 4; б) 0; 1; 2; 3; 4.

8. Выпишите все размещения 5-ти букв (a, b, c, d, e) по 3 буквы, если каждая буква в выборке встречается только один раз.

9. Выпишите все перестановки из цифр 2, 4, 6.

10. Вычислите 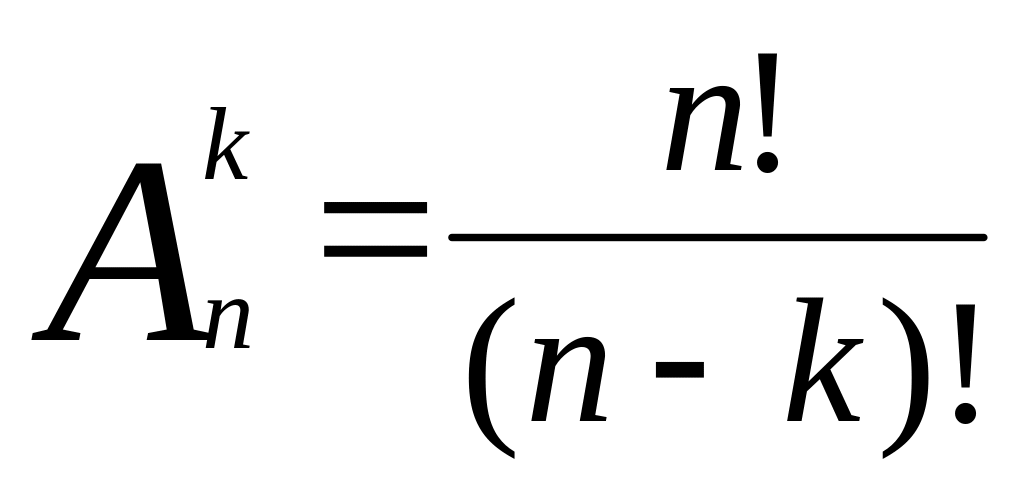и 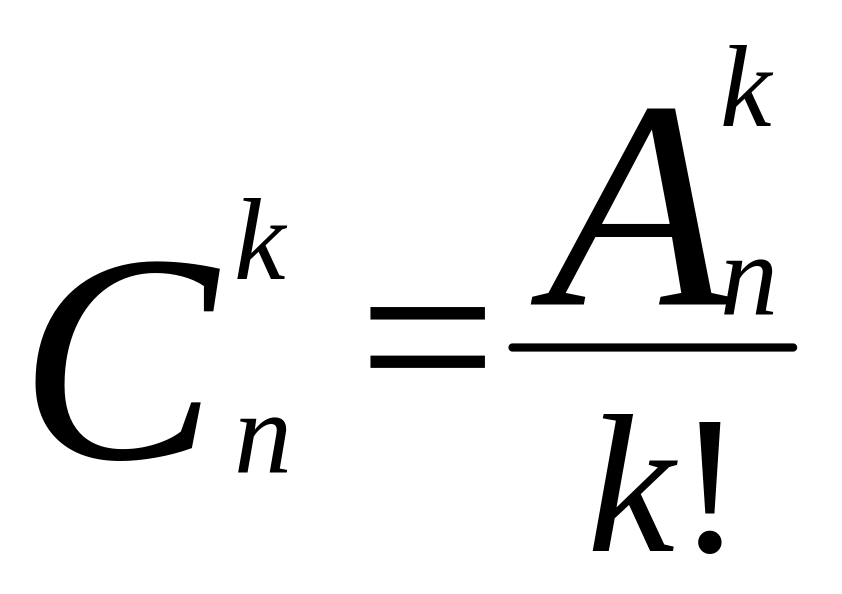, если n=5, k=3.

11. Определите, при каком значении k (0 ≤ k ≤ 5) будет выполняться равенство =P₅ Ответ обоснуйте.

Варианты ответов: а) k=4; б) k=1; в) k=5.

12. В таблице выписаны все размещения из трех букв a, b, c по две буквы (каждая буква в выборке встречается только один раз). Впишите в клетки (1) и (2) пропущенные пары, выбрав из предложенных верный вариант заполнения клеток.

ab	ba	(1)
ac	(2)	cb

Варианты ответов:

а) (1) — сa, (2) — bc; б) (1) — cb; (2) — bc; в) (1) — bc; (2) — ca.

13. Определите, чему равно число элементов исходного множества (n) и число элементов выборки (k) в следующих задачах:

1) Сколько различных двузначных чисел можно составить из цифр 2, 3, 4, 6, 8, если цифры в записи числа не повторяются?

Варианты ответов: а) n=5, k=2; б) n=2, k=5.

2) Из пяти человек надо выбрать двух для участия в финальных соревнованиях. Сколько возможно вариантов?

Варианты ответов: а) n=2, k=5; б) n=5, k=2.

14. Определите, в какой из задач предыдущего задания имеет значение порядок элементов в выборке. Ответ обоснуйте.

15. Подберите формулы для решения задач задания № 13, следуя предложенному алгоритму. Ответ обоснуйте.

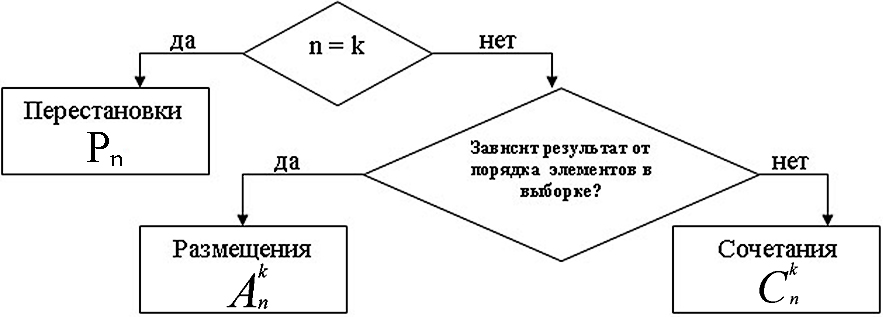
16. Решите следующие задачи, следуя предложенному алгоритму.

1. Сколько различных пятизначных чисел можно составить из цифр 5, 4, 3, 2, 1, если цифры в числе не повторяются?

Варианты ответов: а) 120; б) 60; в) 20.

2. В забеге на ипподроме участвуют 7 лошадей. Известно, что эти лошади всегда показывают разные результаты. Сколькими способами могут распределиться 3 первых места?

Варианты ответов: а) 210; б) 35; в) 820.

3. В группе 21 студент. Сколькими способами можно выбрать 3-х делегатов на студенческую конференцию?

Варианты ответов: а) 420; б) 1330; в) 133.

4. Флаг состоит из трех вертикальных полос одинаковой ширины. Сколькими способами, используя три цвета, можно составить трехцветный флаг?

Варианты ответов: а) 4; б) 8; в) 6.

5. На карточке спортлото 36 клеток. Играющий должен отметить 5 из них. Каково число всех возможных вариантов?

Варианты ответов: а) ; б) 36!; в) .

6. В запасниках музея есть 5 редких книг. На выставку надо выбрать любые 3 из них. Сколько возможно вариантов?

Варианты ответов: а) 120; б) 10; в) 60.

7. Вычислите количество анаграмм, которые можно составить из слова ТОЧКА.

Варианты ответов: а) 120; б) 60; в) 80.

2. Выпишите все размещения из четырех цифр 0, 1, 2, 3 по две цифры. Сколько различных двузначных чисел при этом получится?

Варианты ответов: а) 12; б) 8; в) 9.

3. Определите, какое из следующих равенств является верным:

1) Р₈=6´Р₇

2) Р₅=5´Р₄ .