8

СОДЕРЖАНИЕ

Тема II. Элементы комбинаторики 2

1. Справочные материалы и примеры 2

1.1. Примеры 2

2. Основные определения, обозначения и формулы 3

3. Правила комбинаторики 4

4. Рекомендации для самостоятельной работы 5

5. Задания для самостоятельной работы 5

Тема II. Элементы комбинаторики

(структуры на множестве)

Комбинаторика — раздел математики, в котором изучаются задачи выбора элементов из заданного конечного множества и размещения этих элементов в каком-либо порядке. Поэтому данная тема, с одной стороны, логически продолжает тему «Множества», т.к. задачи комбинаторики — это задачи о конечных множествах и их подмножествах, а с другой — служит основой для решения задач по теории вероятностей, когда нужно уметь подсчитывать число различных комбинаций, подчиненных тем или иным условиям.

Комбинаторика становится наукой лишь в XVII веке. Большой вклад в ее развитие внесли видные математики Б. Паскаль (1623–1662г.), П. Ферма (1601–1665г.), Г. Лейбниц (1646–1716г.) и др.

Знание основ комбинаторики актуально для молодежи в современном обществе, т.к. является профилактикой к увлечению азартными играми, которые постоянно рекламируются, в том числе и в Интернете.

1. Справочные материалы и примеры

В практической деятельности часто приходится сталкиваться с задачами, где нужно ответить на вопрос, каким числом различных способов можно осуществить требуемое. Такие задачи называются комбинаторными, и связаны они, как правило: 1) с выбором из некоторой группы предметов тех, которые обладают заданными свойствами; 2) с расположением этих предметов в определенном порядке; 3) с расчетом числа возможных комбинаций.

Для решения такого типа задач созданы общие методы и выведены определенные формулы. Рассмотрим примеры таких задач.

1. Примеры

Пример 1. Сколько различных музыкальных фраз можно составить из 4-х различных нот, если не допускать в одной фразе повторений одних и тех же нот. Пусть даны ноты до, ре, ми, фа.

Решение. Для составления произвольной музыкальной фразы возьмем в качестве первой любую из 4-х нот, например, ноту до, тогда второй нотой в музыкальной фразе может быть любая из 3-х оставшихся нот и т.д. Перебирая далее все возможные варианты, получим всего 6 музыкальных фраз, начинающихся с ноты до.

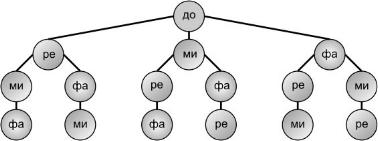
Аналогично надо рассмотреть случай, когда музыкальная фраза будет начинаться с ноты ре, затем — ми, затем — фа. Следовательно, из 4-х различных нот можно составить 24 музыкальных фразы, в которых ноты не повторяются.

Пример 2. Сколько различных музыкальных фраз из 3-х нот можно составить из данных различных 5-ти нот (до, ре, ми, фа, соль), если ноты в ней не повторяются.

Решение. Для составления произвольной музыкальной фразы возьмем в качестве первой любую из 5-ти нот, например, ноту до, тогда второй нотой в музыкальной фразе может быть любая из 4-х оставшихся нот, а третьей — любая из 3-х оставшихся. Для того чтобы учесть все варианты, составим таблицу:

до, ре, ми	до, ре, фа	до, ре, соль
до, ми, ре	до, ми, фа	до, ми, соль
до, фа, ре	до, фа, ми	до, фа, соль
до, соль, ре	до, соль, ми	до, соль, фа

Следовательно, всего 12 различных музыкальных фраз, состоящих из 3-х нот и начинающихся с ноты до. Аналогично в качестве первой можно рассмотреть любую из оставшихся 5-ти нот и вычислить общее количество 125=60 музыкальных фраз, удовлетворяющих условиям задачи.

Пример 3. Сколькими способами можно выбрать 3-х человек для участия в эстафете, если всего в команде 5 человек?

Решение. Пусть каждый из членов команды имеет номер, соответственно №1, №2, №3, №4, №5. Для выбора команды возьмем в качестве первого участника спортсмена № 1, тогда вторым в команде может быть любой из 4-х оставшихся спортсменов, а третьим — любой из 3-х оставшихся. Для того чтобы учесть все варианты, составим таблицу:

№1, №2, №3	№1, №2, №4	№1, №2, №5
№1, №3, №2	№1 №3 №4	№1, №3, №5
№1, №4, №2	№1, №4, №3	№1, №4, №5
№1, №5, №2	№1, №5, №3	№1, №5, №4

Поскольку речь идет о спортсменах, то №1, №2, №3 и №1, №3, №2 — это одна и та же команда, поэтому надо полученное число вариантов разделить на 2, следовательно, всего возможно 6 вариантов. Аналогично рассмотрим в качестве первого спортсмена № 2, тогда можно составить команды: №2, №3, №4: №2, №3, №5; №2, №4, №5; и если в качестве первого выбрать спортсмена №3, то получим еще один состав команды: №3, №4, №5. Таким образом, получим всего 10 различных команд.