Основные механические характеристики материалов

М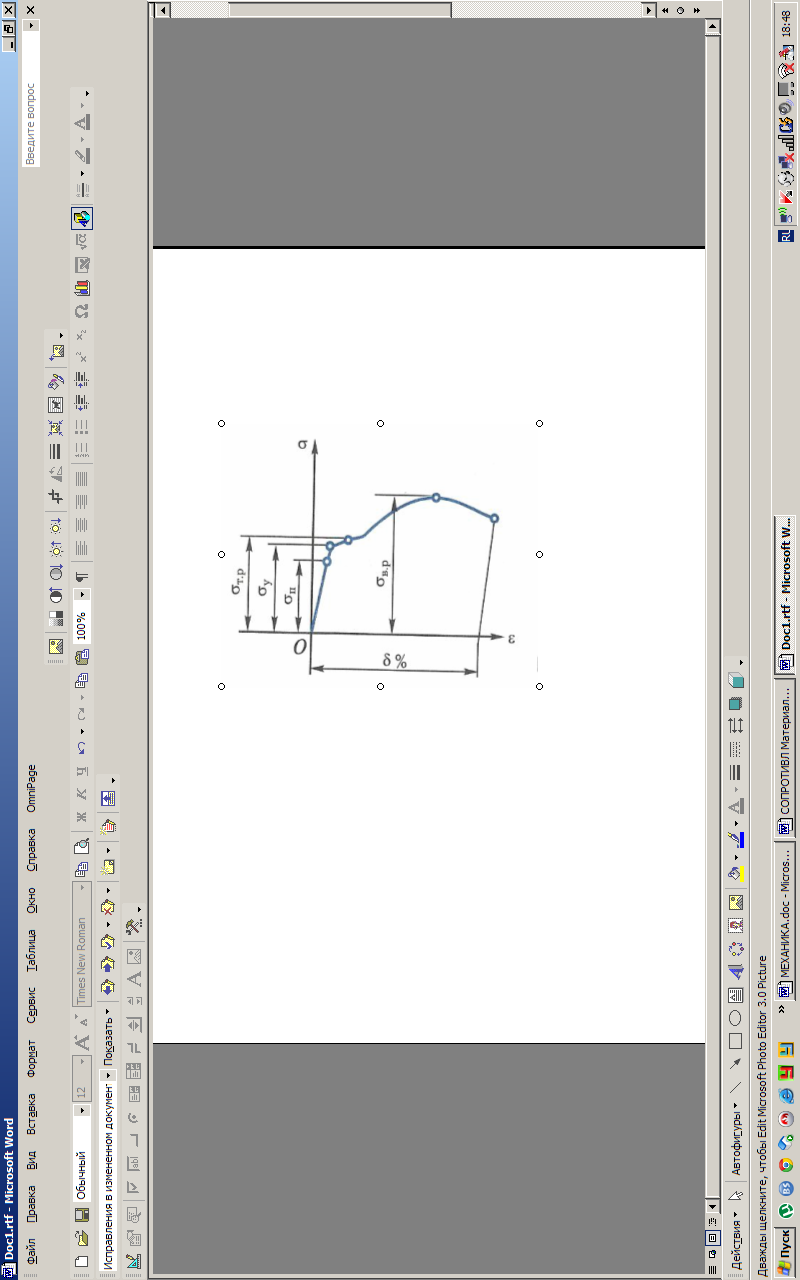 еханические характеристики материалов определяются по результатам испытаний образцов на растяжение. Измерительная диаграмма представляется в координатах  - ε (рис.2.4).

Рис.2.4. Диаграмма растяжения стержневого образца

из низкоуглеродистой стали

Как видно из рисунка, упругие свойства образца сохраняются до напряжения _у – предела упругости, а действие закона Гука – до предела пропорциональности _п. При напряжении _т, называемом предел текучести (несколько большем, чем _у) материал начинает течь, т.е. у него растет остаточная деформация без увеличения нагрузки. Предел текучести легко определяется экспериментально и приводится в справочниках (индекс «р» указывает на принадлежность к деформации растяжения).

За участком текучести следует зона упруго-пластических деформаций с наибольшим значением напряжения _в – временное сопротивление (предел прочности), после которого на образце образуется шейка и он разрушается. Значение _в также приводится в справочниках. Кроме того, указывается величина относительного удлинения при разрыве δ%.

Расчеты на прочность при растяжении и сжатии

Размеры конструктивных элементов должны обеспечивать необходимую прочность при наименьшем расходе материала. При анализе находится в наиболее нагруженном (опасном) сечении точка, в которой возникают наибольшие напряжения _max. Это напряжение не должно превосходить допускаемого напряжения [] для данного материала и конструкции.

Величина допускаемого напряжения назначается с учетом условий работы конструкции и свойств конструкционного материала, которые учитываются при выборе коэффициента запаса прочности п = 1,3 – 5

или , (2.4)

при этом в качестве предельных значений напряжений в формулах (2.4) для пластических материалов принимается предел текучести s_т, а для хрупких, у которых зона текучести отсутствует, принимается предел прочности s_в.

Размеры конструкционного элемента рассчитываются по условию прочности, в рассматриваемом случае на растяжение

. (2.5)

Из решения этого неравенства с учетом уравнения (2.1) находят размеры поперечного сечения стержня для выбранного материала - в случае проектного расчета или оценивают рабочие напряжения на соответствие допускаемым - при проверочном расчете.

2.3. Изгиб

Изгибом называют такой вид деформирования бруса, при котором внешние нагрузки действуют перпендикулярно к его оси и в поперечных сечениях бруса возникают изгибающие моменты. Брус, работающий в основном на изгиб, называют балкой. Если все внешние нагрузки действуют в одной плоскости, то такой изгиб называется плоским изгибом - далее рассматривается только плоский изгиб. Если изгибающий момент является единственным силовым фактором, а поперечные и продольные силы отсутствуют, такой изгиб называют чистым.

На балку могут действовать сосредоточенные силы и моменты, а также распределенные по длине силы с интенсивностью q (размерность Н/м). Анализ внутренних силовых факторов начинают с определения полной системы внешних нагрузок.