2.2. Растяжение и сжатие стержня

Центральным растяжением (сжатием) называется такой вид деформирования, когда все внешние нагрузки действуют вдоль оси стержня, а в поперечных сечениях возникают только продольные (нормальные) силы N.

Закон Гука

Исследования твердых тел показали, что в большинстве случаев деформации растяжения-сжатия в определенных пределах пропорциональны действующим силам. Этот закон пропорциональности напряжения и деформации установил современник Ньютона Роберт Гук и в настоящее время он записывается в виде

, (2.2)

где Е – модуль продольной упругости (модуль Юнга), определенный как отношение нормального напряжения к соответствующей относительной линейной деформации стержня; - относительная линейная деформация растяжения-сжатия при одноосном напряженном состоянии для образца первоначальной длиной l; Δl – удлинение (укорочение) стержня под действием приложенной силы.

Одновременно с продольной деформацией наблюдается и деформация бруса в направлениях, перпендикулярных его оси – поперечные деформации. Если обозначить через b характерный размер поперечного сечения, то поперечная деформация при растяжении определяется уравнением

.

Поперечные и продольные относительные деформации связаны между собой зависимостью

, (2.3)

где μ < 1 – коэффициент Пуассона.

В таблице 2.2 приведены значения модулей упругости и коэффициентов Пуассона для основных конструкционных материалов.

Таблица 2.2

Модули продольной упругости

Наименование материала	Модуль упругости Е, МПа	Коэффициент Пуассона
Сталь углеродистая Чугун Сплавы алюминия Медь	2,1 ∙ 105 (1,15 – 1,6) ∙ 105 0,72 ∙ 105 (1,0 – 1,3) ∙ 105	0,24 – 0,30 0,23 – 0,27 0.26 – 0,36 0,31 – 0,34

В соответствии с уравнениями (2.1) и (2.2) абсолютная величина упругой деформации стержня постоянного сечения под действием осевой нагрузки F определяется зависимостью

, (2.3)

где А – площадь поперечного сечения стержня.

Построение эпюр

Диаграммы изменения нормальной силы, напряжений и перемещений стержня вдоль его оси называются эпюрами соответственно продольных (нормальных) сил, напряжений и перемещений.

Рассмотрим пример построения таких эпюр для стержня, изображенного нна рис.2.3. Начало координат О принято в неподвижном сечении (в заделке), а ось координат z совпадает с осью стержня и направлена вниз.

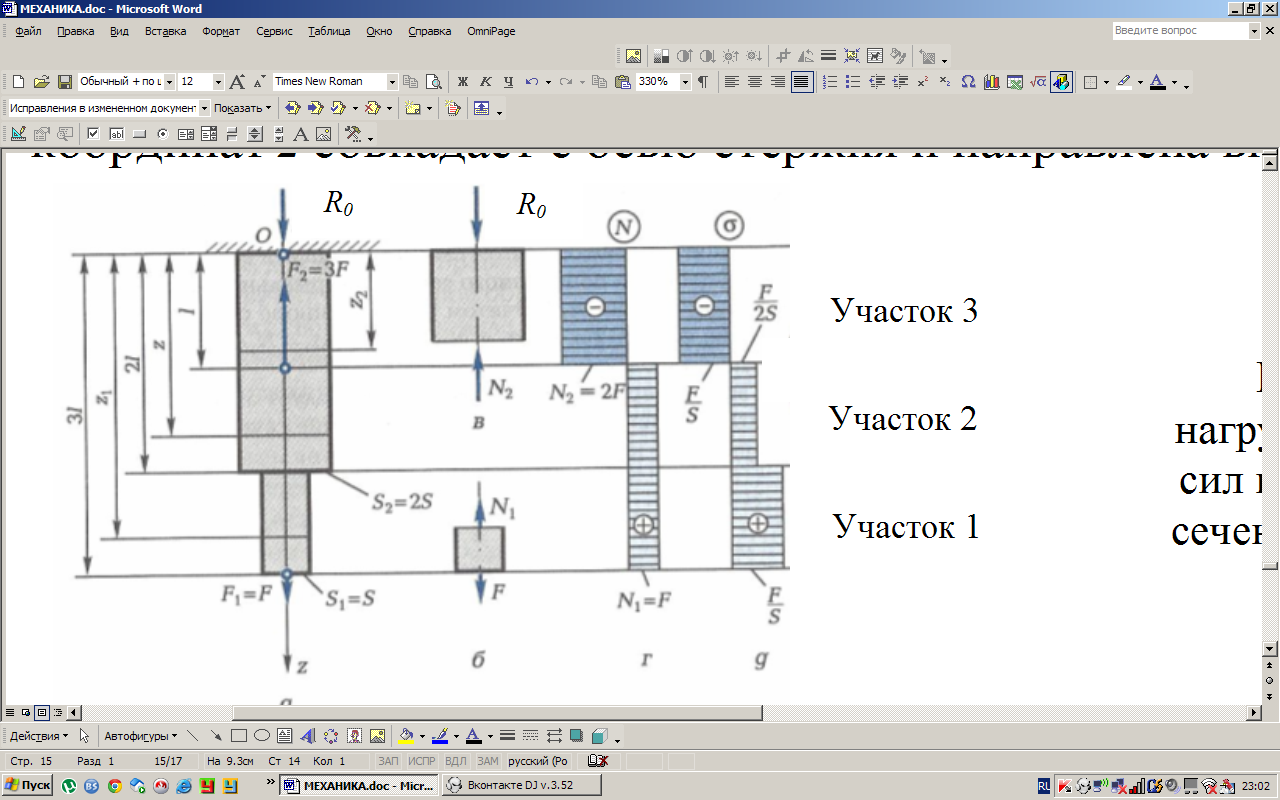
Рис.2.3. Стержень под действием осевых

нагрузок и эпюры продольных (нормальных)

сил и напряжений при площади поперечного

сечения стержня на участках А₁ = S, A_2,3 = 2S

Из уравнения равновесия стержня определяем силу R₀ реакции связи в заделке

Z = 0: R₀ – 3F + F = 0, откуда найдем R₀ = 2F.

При построении эпюр используется метод сечений по участкам, различаемым по размерам поперечных сечений и внешним силовым факторам. В рассматриваемой задаче таких участков три (рис.2.3,а): 1 – от свободного конца стержня до перепада поперечного сечения на больший размер (на интервале расстояний 2l … 3l ); 2 – от первого участка до места приложения силы 3F (на интервале расстояний l … 2l от заделки); 3 - от заделки до места приложения силы 3F (на интервале 0 … l);

Для построения эпюры внутренних продольных сил N на первом участке запишем уравнение силового равновесия для любой отсеченной его части на расстоянии z₁ (рис.2.3,б):

Z = 0: - N₁ + F = 0, откуда находим N₁ = F.

Аналогично найдем для второго участка N₂ = F и для третьего участка N₃ = 2F. По результатам этих расчетов построена эпюра продольных сил (рис.2.3,г).

С учетом эпюры продольной силы строится эпюра нормальных напряжений в поперечных сечениях на участках 1-3 (рис.2.3,д) в соответствии с уравнением , где А_i – площадь поперечного сечения стержня на i-м участке.