Метод конечных элементов
Матричный метод перемещений позволяет составить расчетный алгоритм вплоть до получения усилий во всех элементах рассчитываемой системы и поручить все вычисления ЭВМ. Но для этого вначале необходимо вручную составить исходные матрицы A, k и векторы P, S0. Для сложных систем эта работа довольно трудоемкая.
В
методе конечных элементов также
получается разрешающая система уравнений
KZ
= P,
но матрица жесткости K
вычисляется не по известной формуле K
= AkAT,
а путем суммирования матриц внешней
жесткости отдельных элементов Kэ,
т.е.
,
где
,
а после определения перемещений Z
усилия вычисляются поэлементно по
формуле
,
где вектор усилий Sэ,
матрица усилий
и
вектор перемещений Zэ
относятся
к элементу.
Такой подход позволяет один раз получить матрицы жесткости типовых элементов, произвольно расположенных в пространстве, составить алгоритм расчета и программу, по которой ЭВМ выполнит всю работу по вычислению элементов матриц Kэ, их суммированию, т.е. составлению ансамбля элементов. Название метода отражает его главную идею – представление конструкции как совокупности отдельных конечных элементов, соединенных между собой в узлах, в которых приложены внешние силы.
На плоскости типовые конечные элементы могут быть только трех типов:
шарнирно-стержневой элемент,
балочный защемленный элемент,
балочный комбинированный элемент.
Любую, самую сложную конструкцию на плоскости можно представить как совокупность названных элементов. Следовательно, задача состоит в построении матриц жесткости Kэ для трех типовых элементов.
Отметим одну принципиальную особенность. В ММП рамных систем, как и в методе перемещений, осевыми деформациями стержней пренебрегают. В основной системе закрепляют узлы от поворотов и вводят связи, препятствующие линейным перемещениям узлов соответствующей шарнирной схемы. В МКЭ этого сделать принципиально невозможно, т.к. при произвольном перемещении концов балочного элемента обязательно возникают осевые деформации. Следовательно, в основной системе МКЭ следует закреплять каждый узел как от угловых, так и от линейных перемещений, соответственно увеличивается число неизвестных перемещений. Поэтому результаты расчета по ММП и МКЭ в общем случае не должны совпадать, хотя для реальных конструкций, состоящих из элементов с большой осевой жесткостью, и должны быть близки.
При
построении матриц жесткости
стержневых элементов в МКЭ, как и в ММП,
удовлетворяются уравнения равновесия
(матрица А),
физические уравнения (матрица k),
уравнения неразрывности (матрица В
= АТ),
поэтому перемещения узлов системы,
найденные из разрешающей системы
уравнений KZ
= P
будут точно отражать поле перемещений.
Так же точно находятся деформации и
усилия в элементах. Следовательно, МКЭ
является точным методом расчета
стержневых систем, естественно, в
пределах точности гипотез, лежащих в
основе расчета стержневых систем.
Точно такой же путь решения задач строительной механики в МКЭ для систем из пластин, оболочек, объемных элементов. Конечными элементами для таких систем служат плоские треугольные, прямоугольные, изопараметрические (с криволинейными краями) элементы, либо объемные – тетраэдры, параллелепипеды с разным числом узловых точек. При вычислении матриц жесткости континуальных элементов не удается получить точные решения, поэтому МКЭ для континуальных систем является приближенным методом. Повышение точности решения при расчете континуальных систем достигается за счет более мелкого разбиения конструкции на элементы или за счет применения элементов более высокой точности.
В последнее время появились пакеты МКЭ, упрощающие систему моделирования задач до предела. К примеру, программа COSMOS/DesignSTAR, ориентированная больше на машиностроительные расчеты, допускает введение чертежа конструкции в виде любого CAD-файла, затем, имея в библиотеке всего один элемент в виде тетраэдра, дает запрос – как разбить конструкцию на элементы – грубо или мелко? После выбора расчетчиком степени разбивки на элементы и задания нагрузок все остальное машина делает автоматически.
В пособиях [14], [6] обсуждались вопросы рациональной нумерации узлов конструкции для сокращения объема требуемой памяти машины. Здесь мы делать этого не будем, т.к. современные программные комплексы даже на машинах средней мощности позволяют решать большие задачи. Так программа COSMOSM 2.5 на машинах с оперативной памятью 64 МБ позволяет вести расчет систем, имеющих до 1млн узлов или элементов.
Приведем сравнительную таблицу алгоритмов ММП и МКЭ.
ММП |
МКЭ |
Sок = S + S0. |
|
.
Лекции №18
Теорема о единственности решения (сформулировал Саймондс).
Является синтезом первых двух, устанавливающих пределы снизу и сверху для разрушающей нагрузки и может быть сформулирована так:
Если для заданной системы и схемы загружения существует статически допустимое поле распределения моментов, причём моменты в поперечных сечениях, равные Мпл , образовались в числе точек, достаточных для того, чтобы вся система или какая-либо её часть превратились в механизм, то соответствующая этому распределения моментов нагрузка является действительно разрушающей. Необходимо подчеркнуть, что эта теорема говорит о статически допустимом (а не кинеатически допустимом) поле, т.е. условия неразрывности могут и не выполняться, что имеет место, например, при частичном разрушении. Другими словами, упругий расчёт, в котором используются и статические и геометрические уравнения, не надо! при построении статически допустимого поля; позже на примерах будет показано, что упругий расчёт для построения статически допустимого поля непригоден (при частичном разрушении).
Решение задач пластического расчёта осуществляется с использованием этих трех теорем – статическим и кинематическим методами. О статическом методе мы уже говорили. Он трудоёмок и мы им практически пользоваться не будем. Рассмотрим кинематический метод. Он основан на кинематической теореме и проверяется теоремой о единственности. Для каждого возможного механизма разрушения записываем уравнение равновесия в форме работ всех внешних и внутренних сил на тех перемещениях, которые оказываются возможными для данного механизма после образования пластических шарниров.
При этом работа внешних сил Рi считается положительной и равной полному произведению силы на соответствующее перемещение, т.к. возможная работа (силы считаются при этом постоянными), а работа внутренних сил, те. предельных изгибающих моментов Мпл , возникающих в пластических шарнирах отрицательной и равной произведению Мпл на угол поворота (отрицательна, т.к. внутренние силы препятствуют деформациям – противоположны по направлениям углам поворота).
Это можно записать так:
или
Т.к. все линейные δi угловые θк перемещения могут быть выражены через один параметр θ (в силу малости перемещений). На него можно сократить все уравнения и найти предельную нагрузку, если все предельные несущие способности (Мпл или W пл) заданы.
Наименьшая нагрузка является истинной (искомой). Распределённые нагрузки, приложенные к отдельным прямолинейным участкам, при подсчёте работ могут быть заменены их равнодействующими.
Если три пластических шарнира образуются в одном пролёте получим механизм – они м.б. в сечениях с max моментами, т.е. под силой и в заделках.
Пример 1. при внешней нагрузке, равномерно распределённой на каком – то участке, её работа равна работе равнодействующей силы.
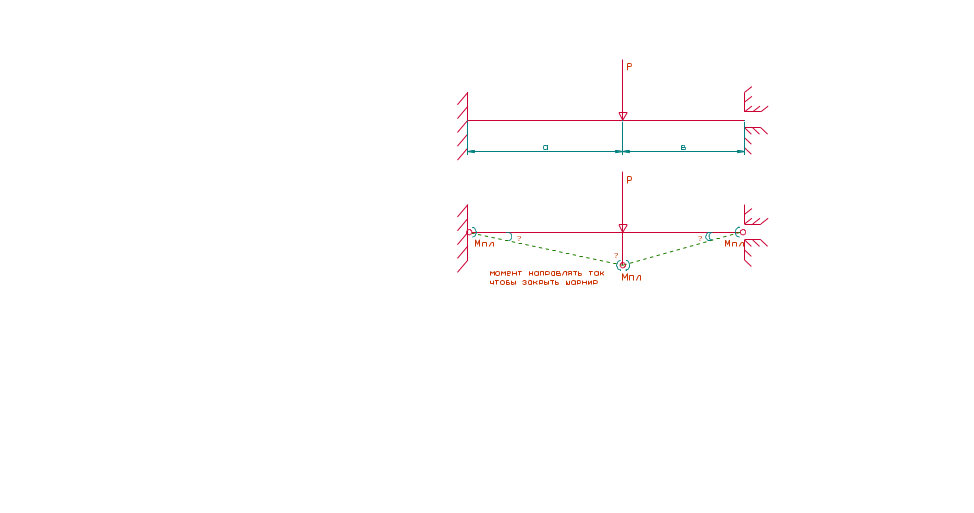
Уравнение равновесия:
δ=аα=вβ=>β=а/вα
отсюда
сократив
на α, получим:
при а=в=l/2 P=8Mпл/l,
что было уже получено статическим
методом. Здесь обратить внимание, что
углы α и β могут быть разными при а≠в
или одинаковыми при а=в
Пример 2. Рама с разными Mпл. Три лишних связи. Возможные схемы разрушения:
а.) частичное. 3 шарнира. 3 пластических шарнира в пролёте, при этом надо смотреть какие изгибающие моменты действуют в них – где тонко там и рвётся ( слева стойка – 0,5 Mпл; справа ригель - Mпл ), поэтому будем рисовать механизм с пластическими шарнирами в тех элементах, кторые разрушаются (хотя они все на одной прямой – на уровне ригеля). 3 Mпл α+0,5 Mплα=Рδ=4α=10,5/12 Mпл (сила 2Р работы не совершает, сократим на α)
Р=3,5/4 Mпл
прикладываем Mпл только к повернувшимся стержням, чтобы легче сост.
Такой механизм называется балочным.
б.) Полное I , 4 шарнира. Опять шарниры в более слабых элементах. Сила Р работы не совершает.
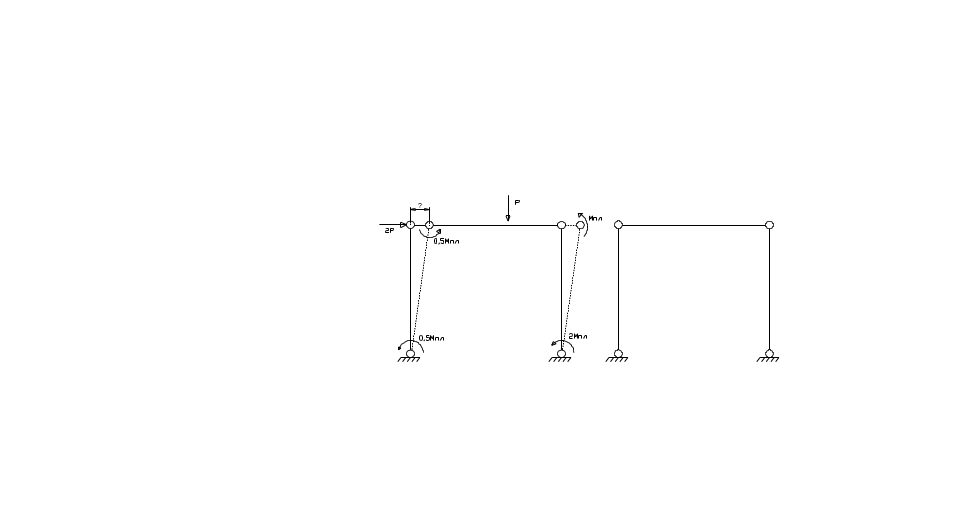
отсюда
сократить на α
Р=2/3 Mпл =8/12 Mпл <Ра ближе к истинному.
в.) Полное II 4 шарнира. Располагаем шарниры в более слабых стержнях
Р=6,5/10 Mпл<Рв
из трёх возможных механизмов последний даёт Рmin
Рmin=0,65 Mпл
Чтобы убедиться, что это действительный механизм разрушения, для него необходимо построить предельную эпюру М, удовлетворяющую условиям равновесия. Если при этом ни в одном сечении М не привысит предельного значения – механизм истинный (по теореме о единственности решения) Откладываем сначала известные моменты в соотв. с механизмом разрушения; неизвестен лишь момент в левом верхнем узле «х», найдём его.
Для нахождения «х» можно использовать одно из трёх следующих уравнений равновесия: (остальные выполняются автоматически. т.к. в уравнения работ вошли они все).
1.)равновесие ригеля – при смещении, т.е. по перерезывающим силам:
ΣХ=0
3,9М=3,5М-Х; Х=-0,4 Mпл., отр – но, Х надо отложить вправо (считаем слева положит.)
2.)из равновесия силы Р:
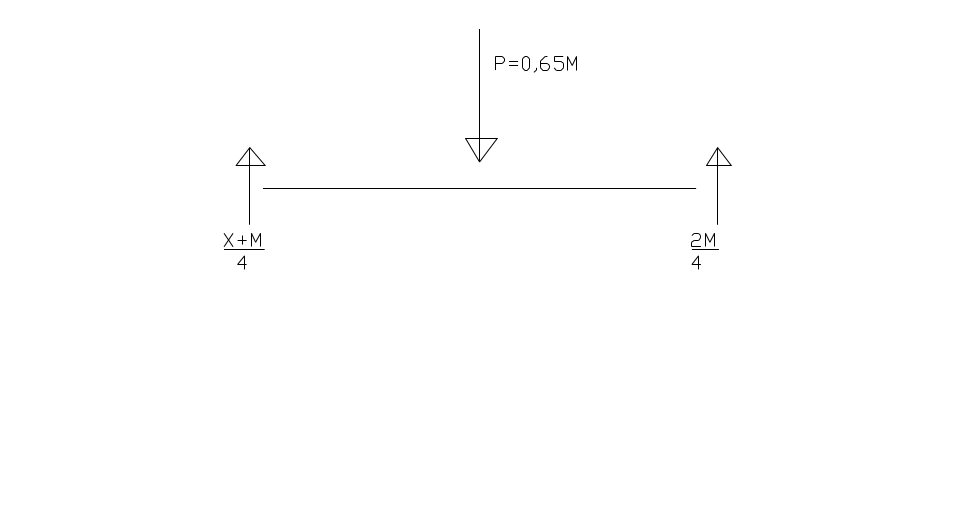
2,6М=Х+3М; Х=-0,4 Mпл (тот же результат)
можно
и так:
откуда Х=-0,4М
можно
и так:
если б не было силы Р, то и М была бы прямой и М в левом узле=3М. М=Р*4=0,65М*4=2,6М
Т.о. получено
Для данной рамы было достаточно просто установить все возможные формы (механизмы) разрушения. Нахождение Рmin не вызывало затруднений. Для более сложных рам основная трудность расчёта состоит в том, что число возможных форм их разрушения м.б. очень велико и заранее не удаётся установить все возможные формы и какая из них является действительной.
Для нахождения действительной и всех возможных форм разрушения м.б. применён метод комбинированных механизмов, предложенный Саймондсом и Нилом.
Согласно этому методу для любой рамы с прямолинейными стержнями (соединёнными под прямыми углами (не обязательно)) при заданной схеме загружения все возможные механизмы разрушения м.б. получены путём составления различных комбинаций относительно малого числа простых независимых механизмов (их число равно числу независимых уравнений равновесия, которое м.б. составлено для рамы, а оно в свою очередь равно m=N-Л, где N – число сечений, в которых необходимо определить момент, чтобы построить эпюру М, а Л – число лишних связей).
Все простые механизмы бывают 3 – х типов6
Балочный (Б)
Бокового смещения (С)
Узловые (У)
в узлах, где больше 2х стержней соединено жёстко. Из последних (У) нельзя найти Рпред т.к. ΣМ внешних сил равна нулю – он говорит лишь о равновесии узла под действием внутренних предельных моментов, действующих в пластических шарнирах, образовавшихся в стержнях, примыкающих к узлу.
При комбинировании механизмов (из простых) следует рассматривать лишь такие комбинации, в которых закрывается хоть один пластический шарнир (уменьшается число внутренних моментов, входящих в уравнение работ, что может привести к уменьшению Рпред) Предельная нагрузка для комбинаций, в которых не закрылся ни один пластический шарнир получится всегда между суммарным Рпред , соответствующих для каждого из комбинированных механизмов (просто сложить оба уравнения для комбинируемых механизмов).
Среди возможных рассматриваемых механизмов разрушения (простых и комбинированных) истинным будет тот, которому при заданных величинах Мпл или W пл соответствует Рmin или при заданной нагрузке Рпред соответствует Мпр max. В первую очередь следует рассматривать комбинации из простых механизмов, для которых значение Рпред является наименьшим, такие комбинации и являются истинными.
Лекции №18
Основы динамики сооружений.
Динамика сооружений –это раздел строительной механики, посвященный методам расчета сооружений на действие динамических нагрузок.
Динамические нагрузки – это нагрузки , изменяющие во времени свою величину, направление, место приложения и вызывающие появление сил инерции масс сооружения.
Цель динамического расчета несущих конструкций промышленных зданий и сооружений – не только обеспечить несущую способность конструкций при совместном действии статических и динамических нагрузок, но и ограничить уровень колебаний пределами, исключающими возможность вредного влияния на людей и технологическое оборудование.
Виды динамических нагрузок:
а
)
неподвижная периодическая нагрузка,
диаграмма зависимости её от времени
многократно повторяется через определенные
промежутки времени (периоды) – создается
механизмами, имеющими неуравновешенные
массы вращающихся частей.
P(t)=
sin
t
-вибрационная
нагрузка
- более общий вид периодической
нагрузки, - гидродинамическое
давление от винтов корабля.
б) подвижная нагрузка на мосты, подкрановые балки ;
в) кратковременные и импульсивные нагрузки, характерные быстрым развитием и быстрым исчезновением – взрывы ;
г) сейсмическая нагрузка – на высотные здания в сейсмически активных районах;
д) ветровая нагрузка – на радио- и телемачты, дымовые трубы, высотные здания;
е) ударная нагрузка – создается падающими телами ( копры, молоты и др.), характерна резким изменением скорости ударного тела в короткий промежуток времени.
Степень свободы в динамике сооружений:
Степенью свободы в динамике называется число независимых геометрических параметров, определяющих положение всех масс системы при упругих деформациях.
Очевидно, что число степеней свободы равно числу связей, необходимых для полного запрещения перемещений масс.
По числу степеней свободы расчетные схемы сооружений при динамическом расчете делятся на системы с конечным и бесконечным числом степеней свободы.
Лекция №19
Системы с одной степенью свободы.
Дифференциальное уравнение движение получим, используя статический метод.
Р(t) – приложенная нагрузка
R= ry - восстанавливающая сила
у
- перемещение, отсчитываемое от положения
статического равновесия (в котором Р=
mg уравновешивается
реакцией балки
.)
r – Коэффициент жесткости, численно равный силе , которую необходимо приложить к балке, чтобы сообщить статическое перемещение, равное единице.
Согласно принципу Даламбера, систему можно рассматривать в состоянии равновесия, если к внешним силам добавить силы инерции.
- сила инерции,
направленная в сторону,
противоположную ускорению.
;
, (1)
где
(2)
При P(t)=0 имеем свободные, или собственные колебания, которые совершает система, выведенная из положения равновесия в результате взаимодействия с каким-либо другим физическим телом после прекращения взаимодействия.
Решим уравнение
(1). Решение ищем в виде
Сила сопротивления R , или восстанавливающая сила, пропорциональна отклонению массы и всегда направлена в сторону статического равновесия.
Сила инерции всегда направлена в сторону противоположную ускорению.
При переходе стержня из положения равновесия в крайнее положение движение происходит замедленно и силы инерции направлены о т линии равновесия ; при обратном движении последнее происходит ускоренно, поэтому силы инерции опять будут направлены в сторону от линии равновесия.
Следовательно, силы инерции всегда направлены в сторону от линии статического равновесия.
Характеристическое
уравнение
(паре
комплексно сопряженных корней
соответствуют решения cos
и sin
).
Решение уравнения
имеет вид:
y(t)= A cos + B sin (3)
Пример:
определить
Лекция №20
Колебания систем с n степенями свободы.
Дифференциальные уравнения движения.
Рассмотрим невесомую балку с сосредоточенными массами, находящуюся под действием вынуждающей нагрузки Р(t).
Согласно
принципу Даламбера систему можно
рассматривать в состоянии равновесия,
если к внешним силам добавить силы
инерции
.
Обозначим
(1) и запишем выражение для прогиба
каждой массы ,который получается от
действия всех сил. Ограничимся написанием
одного уравнения, положив , что i=1,…n
(2)
С учетом (1) уравнение (2) принимает вид:
(3)
Где
Система дифференциальных уравнений (3) описывает вынужденные колебания системы с n степенями свободы.
Свободные колебания. Вывод векового уравнения для определения частот
собственных колебаний.
Дифференциальные
уравнения движения свободных колебаний
получим из (3), полагая
,
для случая n=3 (три
степени свободы).
(4)
-
перемещение массы i от
силы Р=1, приложенной к массе j
,определяемые по формуле Мора.
Решение (4) представим
в виде
(5),
Решением уравнения
является sin(
)
Рассмотрим одно из частных решений (5)
,
которые подставим в (4) , сократив на sin( ) и опустив индекс с i.
(6)
Система однородных линейных алгебраических уравнений (6) имеет два вида решений:
1)
- тривиальное решение, при котором
колебаний не происходит
2)
(не все амплитуды одновременно равны
нулю)
Это возможно лишь
тогда, когда определитель, составленный
из коэффициентов при
равен нулю. Введем обозначение
и запишем определитель:
=0
(7)
Уравнение (7) впервые было получено в астрологии. Характеристические числа в нем, представляющие собой квадраты периодов движения планет, измеряются весьма большими числами- векам, поэтому данные уравнения получили название векового уравнения.
Раскрывая определитель, получаем уравнение 3-ей (n-ой) степени и при его решении n значений частот. В теории колебаний доказывается, что решением (7) всегда являются только положительные числа.
Совокупность всех частот называется спектром частот, первая низшая частота называется основной.
Каждому значению
соответствует свой вектор
, то есть своя форма колебаний ,
а
их совокупность образует матрицу
векторов: у =
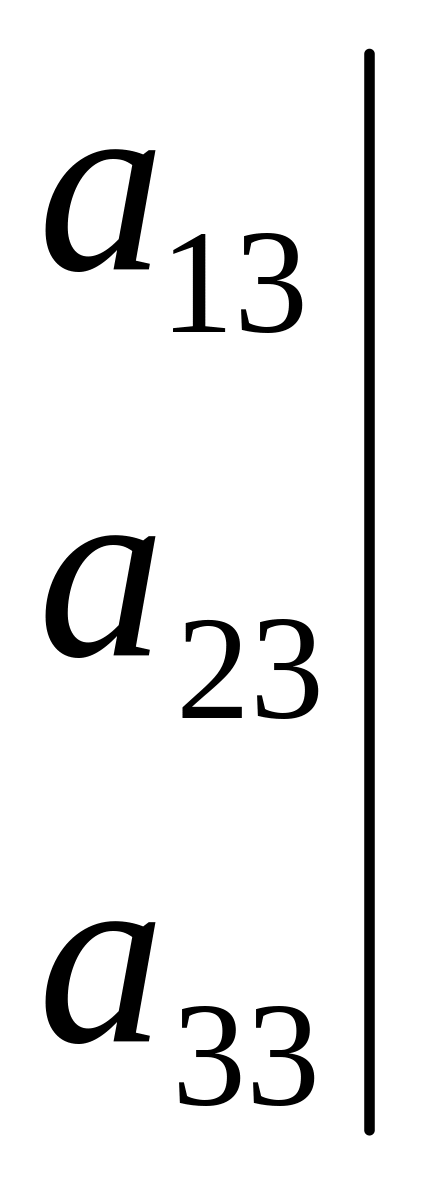
Лекция №21
Вынужденные колебания системы с одной степенью свободы.
Дифференциальное уравнение движения и его решение:
или
(1)
(2)
При действии возмущающей нагрузки Р(4) движение упругой системы складывается из свободных и вынужденных колебаний; причем по прошествии некоторого времени остаются лишь вынужденные колебания, а свободные под действием различного рода сопротивлений затухают.
Таким
образом
(2а)
u- переменное значение времени, меняющееся от 0 до t.
Далее рассмотрим влияние различных видов динамических воздействий : периодическую нагрузку, постоянную силу долговременно и кратко временно действующую, импульс, удар.
1.
Действие вибрационной нагрузки .
Решение
уравнения движения можно получить
исходя из общего решения при произвольной
величине P(t)
, но здесь проще задавать
,
, подставляя у и
,
получим
,
а отсюда определим
; т.к
,то
- статический
прогиб .
-
динамический коэффициент, показывающий
во сколько раз динамические перемещения
от силы
больше перемещений от статической силы
График динамического коэффициента :
При
<
>0
вынужденные колебания происходят в
той же фазе, что и возмущающая сила
При >w <0 колебания силы и системы происходят в противоположных фазах .
При
=
имеем случай резонанса (совпадение
частот) .
неограниченно возрастает амплитуда
вынужденных колебаний .
Для расчета на резонанс следует с самого начала положить = , тогда отыскивая решение уравнения в виде y=Btsinwt , получаем
Лекция№22
Энергетический метод определения частот собственных колебаний (метод Релея).
Основан метод на
законе сохранения энергии. Процесс
колебания рассматривается , как процесс
постоянного преобразования кинетической
энергии-К в потенциальную - П. Когда
система достигает крайних положений
К=0, П=max, а когда проходит
через положение статического равновесия
К=max, П=0. Сумма К+П=const,
а следовательно
.
(очевидно, что затухание не учитывается)
Порядок расчета:
1.Задают уравнение
перемещений
y(x)- наибольшее отклонение от положения равновесия.
2. Вычисляют П.
;
3.Вычисляют k.
4. Определяют
(1)
или
(2)
Если система имеет
гибкие безмассовые участки , то в
выражении для потенциальной энергии
добавляется член
, где
-
эпюра моментов для гибкой части при
амплитудном отклонении масс.
Формулой (2) рекомендуется пользоваться для систем с одной степенью свободы, но с несколькими массами.
Формулой (1) можно пользоваться для определения w систем с бесконечным числом степеней свобод ,в этом случае П вычисляется , как потенциальная энергия деформации связанная с изгибом.
;
, а выражение (1)
принимает вид:
(3)
Точность результата
зависит от удачного задания формы
колебаний, если форма задаваемая
совпадает с действительностей, то
получают точное решение как например,
для шарнирно опертой балки, если y(x)=sin
. При случайно задаваемых кривых частота,
определяемая энергетическим методом
, всегда выше истинной.
Для системы упругой с несколькими массами, например,
Потенциальную
энергию деформации можно выразить через
работу внешних сил P=m
на перемещениях
.
, тогда формула
(1) принимает вид:
Пример:
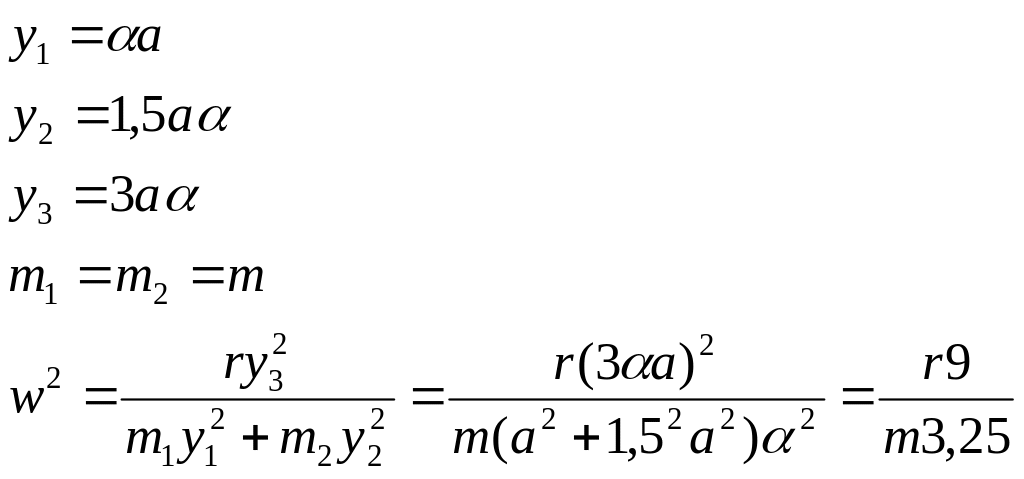
Пример:
П
ример:
Определить амплитуду вынужденных
колебаний в т. В.
y(x)=dx
;
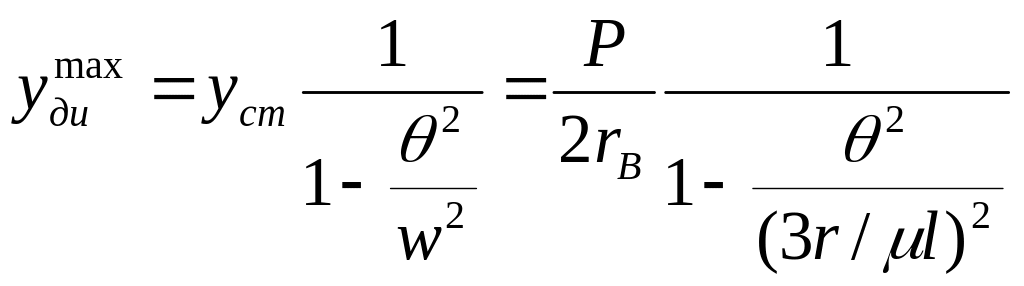
Лекция №23