Кинематический анализ конструкций с помощью матрицы а

Статическая матрица А имеет размер mn, где m – число строк, равное числу возможных перемещений узлов, n – число столбцов, равное числу внутренних усилий.

1. При m  n система изменяема, причем число степеней свободы W = m – n.

2. При m = n система неизменяема и статически определима, если ее определитель При система мгновенно изменяема.

3. При m  n система неизменяема и статически неопределима, если ранг матрицы равен числу строк. Число лишних связей л = n – m.

Как видно из (2.3), статическая матрица А имеет размер 45, следовательно m = 4, n = 5, m  n, система статически неопределима и имеет одну лишнюю связь, л = n – m = 5 – 4 = 1. Действительно, сняв любой стержень фермы (рис. 2.1), получаем статически определимую систему. Матрица в (2.5) имеет размер 24, система также статически неопределима, число лишних связей л = 4 – 2 = 2.

Как видно из п. 2, в статически определимых системах при m = n матрица А квадратная, поэтому, очевидно, возможно формальное решение матричного уравнения (2.2). Если умножить его слева на обратную матрицу А^-1, то

S = A^-1P . (2.6)

Таким образом, подтверждается возможность и в матричном виде находить все внутренние усилия системы из уравнений статики, что хорошо известно из классической строительной механики. Специальных примеров по расчету статически определимых систем мы давать не будем, т.к. эти системы могут быть рассчитаны по единому алгоритму ММП, а в дальнейшем и МКЭ.

Рассмотрим два примера на кинематический анализ с помощью статической матрицы А.

Лекция №14

Уравнения неразрывности. Матрица деформаций

Установим связь между деформациями элементов e_i и перемещениями узлов системы Z_j, или запишем уравнения неразрывности деформаций. Для этого определим деформации e_i в каждом стержне от действия каждого узлового перемещения Z_k, считая все остальные перемещения равными нулю.

Для фермы, показанной на рис. 2.1, зададим сначала перемещение Z₁, затем Z₂ и определим деформации стержней на рис.2.9.

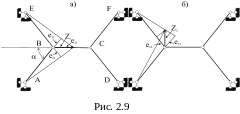
В соответствии с рис. 2.9, а найдем деформации, вызванные перемещениями Z₁:

e₁₁ = Z₁cos, e₂₁ = Z₁cos, e₃₁ = -Z₁,

остальные перемещения е₄₁ = е₅₁ = 0, т.к. узел С не имеет перемещений.

В соответствии с рис 2.9, б найдем деформации, вызванные перемещениями Z₂:

e₁₂ = Z₂sin, e₂₂ = - Z₂sin,

остальные перемещения е₃₂ = е₄₂ = е₅₂ = 0. Точно так же, задавая перемещения Z₃ и Z₄, найдем деформации всех стержней. Просуммировав деформации, вызванные перемещениями Z₁ – Z₄ для каждого стержня, получим

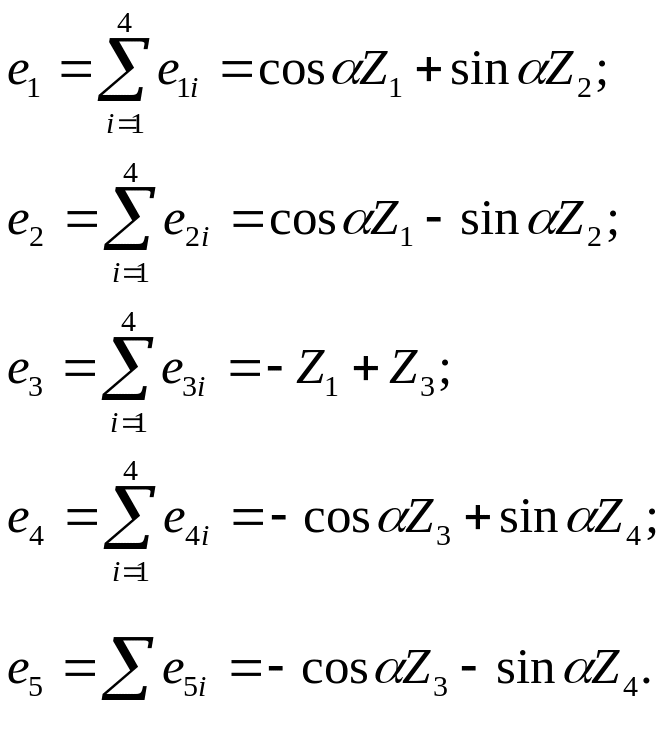(2.7)

Перепишем систему уравнений (2.7) в матричном виде

e = BZ , (2.8)

где e = [e₁ e₂ e₃ e₄ e₅]^T – вектор деформаций элементов, Z = [Z₁ Z₂ Z₃ Z₄]^T – вектор перемещений узлов.

Здесь матрица В – матрица деформаций, выражающая деформации e_i элементов стержневой системы через перемещения Z_k ее узлов. Ее размер m  n, где m – число строк, равное числу деформаций e_i и равное числу неизвестных усилий S_i, n – число столбцов, равное числу возможных узловых перемещений Z_k.

P S	1	2	3	4
1	cos	sin
2	cos	-sin
3	-1		1
4			-cos	sin
5			-cos	-sin

(2.9)

B =

Аналогично строится матрица деформаций для рамных систем, подробнее об этом можно прочитать в [14] и в [5].

Лекция №15