43

Лекция№8

Метод перемещений

В методе сил, изученном в курсе «Строительная механика», за основные неизвестные принимались усилия в лишних связях, для нахождения которых составлялись кинематические уравнения (уравнения неразрывности деформаций), а затем определялись внутренние усилия в сечениях и перемещения в любой точке конструкции, т.е. при расчете статически неопределимых систем методом сил сначала находили силы, а потом перемещения. Можно поступить и наоборот.

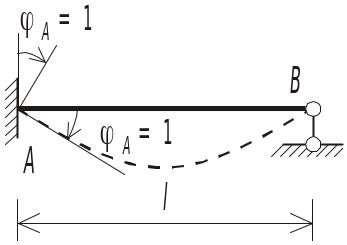
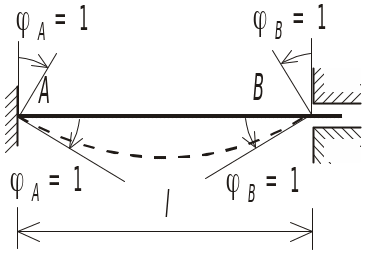
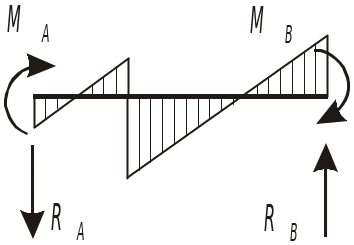
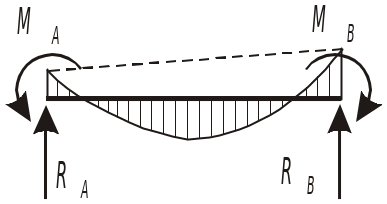
Предположим, что требуется рассчитать раму, показанную на рис. 1.1, а.

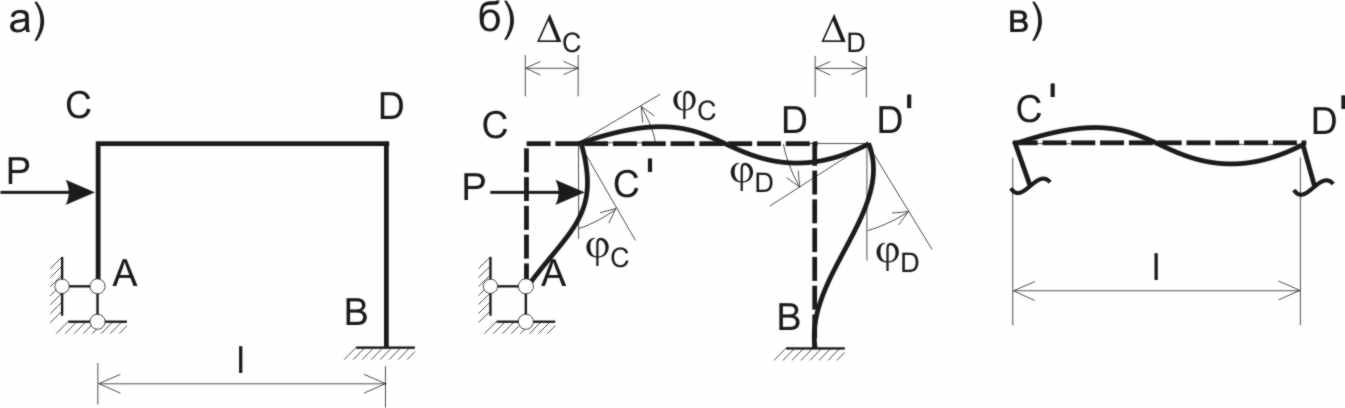
Рис. 1.1

Под действием нагрузки элементы рамы искривляются, а ее узлы получают угловые ( ) и линейные ( ) перемещения (рис. 1.1, б). Если бы удалось каким-либо образом найти эти угловые и линейные перемещения, то по известным формулам сопротивления материалов можно было легко определить и внутренние усилия в любом сечении рамы. Вся проблема состоит в том, как найти эти перемещения.

Метод, в котором за о с н о в н ы е н е и з в е с т н ы е принимаются угловые и линейные перемещения узлов системы и который позволяет их найти, носит название метода перемещений. Этот метод, как и метод сил, является основным для расчета статически неопределимых стержневых систем.

Основные гипотезы метода перемещений

1. Как и в методе сил, пренебрегаем влиянием продольных и поперечных сил на деформации стержней, т.е. учитываем только деформации изгиба.

2. Поскольку все перемещения принимаются малыми, то можно пренебречь сближением концов стержня при его изгибе, т.е. предполагается, что первоначальная длина прямого стержня (см. рис. 1.1, а) до деформации равна длине хорды стягивающей концы стержня после его деформации (рис. 1.1, в).

Из этих гипотез следует, что а точки и будут перемещаться перпендикулярно к стойкам и по отрезкам касательных, проведенных к окружностям радиусов и т.е. по горизонтали, и не могут иметь вертикальных перемещений. Такие же горизонтальные перемещения ( ) имеют и все остальные точки стержня

6.1. Силовое воздействие

Общее число неизвестных метода перемещений называют с т е- п е н ь ю к и н е м а т и ч е с к о й н е о п р е д е л и м о с т и с и с т е м ы и обозначают буквой Она определяется как сумма неизвестных углов поворота и неизвестных независимых линейных перемещений узлов :

(6.1)

Число неизвестных углов поворота равно числу жестких узлов. Под ж е с т к и м у з л о м будем понимать узел, в котором жестко соединено не менее двух стержней.

Число независимых линейных смещений узлов тоже легко определяется по схеме сооружения, но можно и подсчитать эту величину, рассматривая шарнирную схему сооружения, которая получается из заданной системы путем введения шарниров во все жесткие узлы, включая и опорные. Если в заданной системе имеются статически определимые консоли, то они должны быть предварительно отброшены. Необходимо помнить, что, врезая шарнир в жесткую заделку, получаем шарнирно-неподвижную опору, а, врезая шарнир в скользящую заделку, – шарнирно-подвижную опору. Значение для рам с прямыми стержнями равно степени свободы шарнирной схемы W_Ш.СХ :

=W_Ш.СХ = 2УСС₀ , (6.2)

где У – число шарнирных узлов рамы, включая опорные; С – число стержней рамы; С₀ – число опорных связей.

По шарнирной схеме можно определить не только количество линейных смещений, но и их направления.

Определим число неизвестных метода перемещений для некоторых систем.

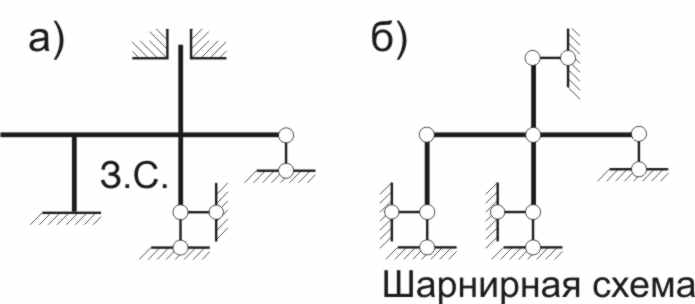Так как рама имеет два жестких узла (рис 1.2, а), По шарнирной схеме (рис. 1, б) определяем : = 2УСС₀= =

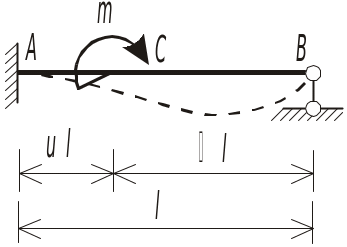
Рис.1.2

Возможно только горизонтальное смещение ригеля.

Степень кинематической неопределимости составляет

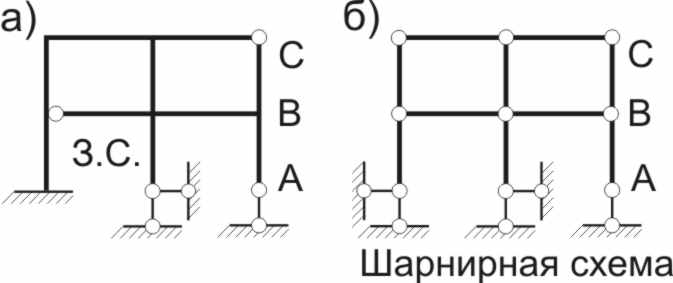
Для рамы, изображенной на рис. 1.3, а, имеем Число определим по шарнирной схеме (рис. 2, б):

= 2УСС₀=

Возможны горизонтальные смещения узлов Общее число неизвестных равно

Рис.1.3

Порядок расчета сооружения методом перемещений аналогичен порядку расчета стержневых систем методом сил. Подсчитав степень кинематической неопределимости системы, вводят в расчет вместо заданной системы основную, но получают ее здесь не отбрасыванием лишних связей, а наложением дополнительных, устраняющих возможные перемещения узлов. Если во все жесткие узлы системы ввести заделки (защемления), препятствующие поворотам узлов, и закрепить узлы от поступательных смещений установкой дополнительных стержней (опорных стержней), то получим в качестве основной системы совокупность независимых однопролетных статически неопределимых балок двух видов: балка с двумя заделками по концам и балка, у которой на одном конце заделка, а на другом – шарнирно-подвижная опора. Эти балки постоянного сечения заранее рассчитаны на все виды воздействий (см., например, задачи для самостоятельного решения в гл. 5 и ответы к ним), и их решения для наиболее часто встречающихся случаев помещены в табл. 1.1.

С помощью табл. 1.1 в дальнейшем весьма просто строятся единичные и грузовые эпюры моментов путем формального переноса соответствующих эпюр моментов из таблицы на деформированные стержни основной системы от различных воздействий.

Число вводимых связей равно степени кинематической неопределимости системы: число дополнительных заделок совпадает со степенью угловой подвижности (количество жестких узлов ), а число дополнительных опорных стержней – со степенью линейной подвижности узлов ( = W_Ш.СХ).

Дополнительная заделка эквивалентна одной связи и отличается от обычной опорной жесткой заделки, которая эквивалентна трем связям, тем, что препятствует только угловым перемещениям узлов и не препятствует их поступательным перемещениям. В дополнительной заделке может возникать в качестве реакции только момент. Эта так называемая моментная, или угловая связь. В дополнительном стержне возникает реакция, направленная по оси этого стержня, – это силовая или поступательная связь.

Поскольку узлы заданной системы под внешним воздействием могли иметь угловые и линейные перемещения, а в основной системе они невозможны, чтобы сделать основную систему эквивалентной заданной по перемещениям и усилиям, надо дополнительно к заданному внешнему воздействию приложить во введенные связи действительные угловые и линейные перемещения, которые пока неизвестны.

Этими перемещениями компенсируется введение дополнительных закреплений, и как раз они являются основными неизвестными метода перемещений, которые обозначаются буквой с подстрочным индексом ( ). Введением неизвестных перемещений в дополнительные связи и определяется окончательная основная система, которую можно назвать к и н е м а т и ч е с к и о п р е д е л и м о й. В дальнейшем изложении она будет изображаться с заданными нагрузками, дополнительными связями и неизвестными перемещениями Отметим, что основная система метода перемещений – единственная.

При расчете симметричных систем методом перемещений, так же, как и при расчете методом сил, можно и нужно применять способ группировки неизвестных, который значительно облегчает расчет.

Таблица 1.1

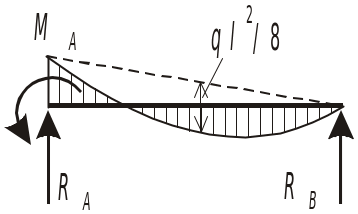
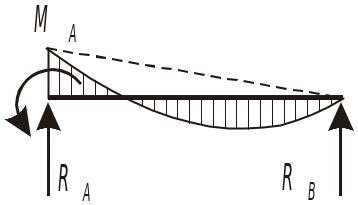
¹ п/п	Схема балки и воздействия на нее		Эпюры изгибающих моментов и реакции		Формулы моментов и реакций
1					– погонная жесткость
2
3					при
4					при 
5
¹ п/п		Схема балки и воздействия на нее		Эпюры изгибающих моментов и реакции		Формулы моментов и реакций
6
7
8
9		Неравномерный нагрев				коэффициент линейного расширения; высота поперечного сечения
10
11

¹ п/п			Схема балки и воздействия на нее			Эпюры изгибающих моментов и реакции			Формулы моментов и реакций
12
13
14									при ;
15									при ;
16
¹ п/п	Схема балки и воздействия на нее			Эпюры изгибающих моментов и реакции			Формулы моментов и реакций
17
18	Неравномерный нагрев						 коэффициент линейного расширения;  высота поперечного сечения

Неизвестные перемещения симметрично расположенных узлов группируются в новые парные неизвестные, представляющие собой симметричные и обратносимметричные перемещения. Группировать можно как угловые, так и линейные неизвестные. В расчетной практике чаще встречаются задачи, в которых группируются только угловые неизвестные. Тогда угол поворота одного узла представляем как сумму двух неодинаковых в общем случае углов, а угол поворота симметричного узла – как их разность. За одно из неизвестных принимается теперь поворот уже не одного, а сразу двух симметрично расположенных узлов на одну и ту же величину и в одном направлении. Поворот этих же узлов на одну и ту же величину в противоположных направлениях принимается за второе групповое неизвестное.

Лекция№9

Cвойства для систем с вертикальной осью:

1. Угловое неизвестное, находящееся на оси симметрии, является обратносимметричным.

2. Вертикальное линейное неизвестное, находящееся на оси симметрии, является симметричным.

3. Горизонтальное линейное неизвестное, направленное вдоль ригеля, является обратносимметричным.

Если заданная система раз кинематически неопределима, то после наложения на нее дополнительных связей, устраняющих возможные перемещения ее узлов и приложения к ним неизвестных перемещений , система канонических уравнений метода перемещений для определения этих неизвестных может быть представлена в виде

 (1.3)

или в матричной форме:

,  (1.4)

где  вектор неизвестных;

 вектор свободных (грузовых) членов;

 матрица внешней жесткости системы, которая в развернутой форме имеет вид

 (1.5)

Все реакции, обозначенные буквой называются единичными реакциями. Так,  реакция, возникающая в дополнительной связи где имеется перемещение от перемещения связи на единицу (от );  реакция, возникающая в дополнительной связи от перемещения связи на величину ;  реакция, возникающая в дополнительной связи где имеется перемещение от смещения этой же связи на единицу ( );  реакция в связи от ее смещения на величину ;  реакция, возникающая в связи от действия на основную систему нагрузки. Первый индекс у и показывает номер связи, в которой возникает реакция, а второй  указывает на причину появления реакции. Реакция, возникающая в связи ( , ), считается положительной, если ее направление совпадает с направлением неизвестного перемещения показанного на основной системе. Еще раз напомним, что реакции, возникающие в дополнительных заделках (защемлениях), называются реактивными моментами, а в дополнительных опорных стержнях,  просто реакциями, или реактивными усилиями.

Поскольку уравнения (1.3), (1.4) являются условиями эквивалентности по усилиям заданной и основной систем (условиями равновесия), ф и з и ч е с к и й с м ы с л любого -го уравнения заключается в том, что суммарная реакция в дополнительной связи от действия всех неизвестных и нагрузки на основную систему равна нулю, потому что в заданной системе эта дополнительная связь отсутствует.

Как и в методе сил, коэффициенты с одинаковыми индексами, расположенные на главной диагонали матрицы (6.5), называются г л а в н ы м и коэффициентами, которые всегда п о л о ж и- т е л ь н ы и не равны нулю. Остальные коэффициенты этой матрицы называются п о б о ч н ы м и. Они могут быть положительными, отрицательными и равными нулю. В соответствии с первой теоремой Рэлея о взаимности реакций между побочными коэффициентами выполняется соотношение

,

вследствие чего матрица внешней жесткости будет симметричной и, как матрица внешней податливости в методе сил, положительно определенной.

Для вычисления коэффициентов при неизвестных и свободных членов канонических уравнений метода перемещений надо сначала построить эпюры изгибающих моментов в основной системе от единичных неизвестных перемещений узлов рамы и от внешней нагрузки. При построении единичных эпюр моментов весьма желательно предварительно показать пунктирной линией характер деформирования оси каждого стержня от единичного угла поворота или линейного смещения, что позволит установить положение растянутых волокон и безошибочно перенести из табл. 6.1 эпюры моментов для отдельных балок на основную систему и тем самым правильно изобразить единичную эпюру моментов в целом.

После построения единичных эпюр моментов и грузовой эпюры моментов переходят к вычислению коэффициентов и свободных членов применяя статический или кинематический (перемножение эпюр) способы.

С т а т и ч е с к и й с п о с о б из-за своей простоты и наглядности является основным способом определения коэффициентов при неизвестных и свободных членов и основан на использовании уравнений равновесия. Особенно просто находятся реакции, представляющие собой реактивные моменты во введенных защемлениях, из условий равновесия вырезанных из основной системы узлов в виде

Несколько сложнее вычисляются реакции, представляющие собой реактивные усилия во введенных опорных стержнях. Для их определения составляются уравнения равновесия некоторой отсеченной части основной системы, содержащей эти силовые связи, в виде

К и н е м а т и ч е с к и й с п о с о б дает возможность находить реактивные моменты и усилия в дополнительных связях аналогично тому, как это делалось в методе сил, т.е. путем интегрирования (перемножения) соответствующих эпюр по формулам, вытекающим из теоремы о взаимности работ:

(1.6)

где , – единичные эпюры моментов, построенные в основной системе метода перемещений; – эпюра моментов от нагрузки, построенная в любой статически определимой системе, полученной из заданной.

В практических расчетах при определении единичных реакций и свободных членов или их проверке кинематический способ из-за трудоемкости вычислений и вероятности появления ошибок не при-меняется. Как исключение он может быть использован для вычисления некоторых коэффициентов при расчете рам с наклонными стойками, когда применение статического способа усложняется.

В то же время формулы (1.6) примечательны тем, что при нахождении коэффициентов уравнений (1.3) можно воспользоваться, как и в методе сил, свойством взаимной ортогональности эпюр моментов, из которого следует, что если одна из эпюр моментов симметрична, а другая – обратносимметрична, то соответствующий коэффициент или свободный член являющийся результатом перемножения этих эпюр, априорно равен нулю.

В симметричных системах разделение неизвестных перемещений на две группы (симметричные и обратносимметричные), как известно, приводит к разделению общей системы канонических уравнений (1.3) на две подсистемы, одна из которых содержит только симметричные, а другая  только обратносимметричные неизвестные. В методе перемещений для таких систем остаются справедливыми и два правила о действии на симметричное сооружение симметричной или обратносимметричной нагрузки.

Подставив найденные коэффициенты и свободные члены в систему (1.3) и решив ее, найдем действительные значения неизвестных метода перемещений После этого окончательную эпюру моментов строим, как и в методе сил, т.е. как алгебраическую сумму эпюры от заданной нагрузки в основной системе и единичных эпюр умноженных на найденные значения неизвестных:

где  исправленная единичная эпюра моментов.

Следует отметить, что как исходные , , так и исправленные эпюры моментов метода перемещений являются неуравновешенными, в то время как окончательная эпюра изгибающих моментов должна быть обязательно уравновешенной. Поэтому необходимым и достаточным условием правильности эпюры является равенство нулю реакций во всех введенных связях при правильных единичных и грузовой эпюрах. Это означает, что все узлы системы должны быть уравновешены, и должны отсутствовать реактивные усилия в дополнительных опорных стержнях. Обычно второе условие (равенство нулю реактивных усилий) сразу не проверяется, а совмещается с проверкой эпюр и

Наряду со статической может быть применена и кинематическая проверка, как это делалось в методе сил. Для этого надо окончательную эпюру моментов умножить на единичные эпюры или на их суммарную, построенные в любой основной системе метода сил, образованной из заданной. При практических расчетах эту проверку, как правило, не выполняют.

После частичной или полной проверки эпюры по обычным правилам строят эпюры поперечных и продольных сил

Окончательной проверкой правильности всего расчета является одновременное выполнение всех трех уравнений статики ( ) как для заданной системы в целом, так и для любых отдельных ее частей.

Последовательность расчета статически неопределимых систем методом перемещений остается такой же, как и методом сил.

Лекция№10