
- •Контрольні роботи з дисципліни «Теорія електричних та магнітних кіл» Контрольна робота 1
- •Методичні вказівки до виконання контрольної роботи Складання системи рівнянь за законами Кірхгофа
- •Метод контурних струмів
- •Метод вузлових потенціалів
- •Баланс потужності кола
- •Контрольна робота 2 Електричні кола синусоїдного струму
- •Методичні вказівки до виконання контрольної роботи Складання системи рівнянь за законами Кирхгофа
- •Розрахунок струмів у гілках
- •Приклад розрахунку
- •Контрольна робота 3 Електричні кола трифазного струму
- •Методичні вказівки до виконання контрольної роботи р озрахунок чотирипровідного кола (мал3-21)
- •Розрахунок трипровідного кола при з’єднанні навантаження зіркою(мал3-22)
- •Контрольна робота 4
- •Методичні вказівки до виконання контрольної роботи Перед початком розрахунку несинусїдна ерс повинна бать представлена рядом Фур'є.
- •Контрольна робота 5 Розрахунок перехідного процесу в розгалуженому електричному колі
- •Методичні вказівки до виконання контрольної роботи Класичний метод розрахунку перехідних процесів
- •Приклад розрахунку
- •Операторній метод розрахунку
- •Приклад розрахунку
- •Контрольна робота 6
- •Методичні вказівки до виконання контрольної роботи
- •Методичні вказівки до виконання контрольної роботи
Контрольна робота 2 Електричні кола синусоїдного струму
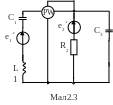
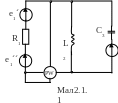
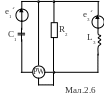
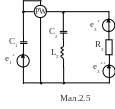
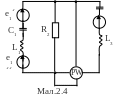
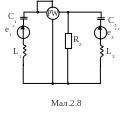
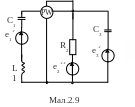
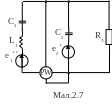
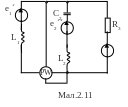
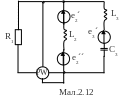
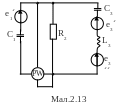
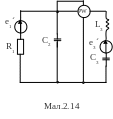
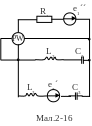
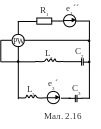
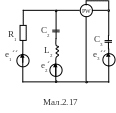
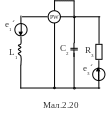
Для електричної схеми, відповідної номеру варіанту (табл.2) і зображеною на
мал. 2.1-2.20, виконати наступне:
1.На основі законів Кирхгофа скласти в загальному вигляді систему рівнянь для розрахунку струмів в усіх гілках кола, записавши її в двох формах:
а) диференціальною;
б) символічною.
2.Определить комплекси діючих значень струмів в усіх гілках, скориставшись одним з методів розрахунку лінійних електричних ланцюгів.
3.По результатам, отриманим в п. 2, визначити свідчення ватметра двома способами: а) за допомогою вираження для комплексів струму і напруги на ватметрі;
б) по
формулі
![]() .
За допомогою векторної діаграми струму
і напруга, на яку реагує ватметр, пояснити
визначення кута
.
За допомогою векторної діаграми струму
і напруга, на яку реагує ватметр, пояснити
визначення кута
![]()
4.Построить топографічну діаграму, поєднану з векторною діаграмою струмів.
При
цьому потенціал точки
![]() ,
вказаної на схемі, прийняти рівним нулю.
,
вказаної на схемі, прийняти рівним нулю.
5.
Використовуючи дані розрахунків,
отриманих в п. 2 , записати вираження для
миттєвого значення струму або напруги
.Побудувати графік залежності вказаної
величини від
![]()

e3´


e3´



Таблиця2
варіант |
Номер схеми |
L1 |
L2 |
L3 |
C1 |
C2 |
C3 |
R1 |
R2 |
R3 |
f |
E |
||
мГн |
мкФ |
Ом |
Гц |
В |
||||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
||
1 |
1 |
- |
34,7 |
- |
- |
- |
80,3 |
17 |
- |
- |
55 |
e'1 =80sin( ωt + 45º) e''1 =80cos( ωt - 135º) e'3 =56,6cos( ωt - 30º) |
||
2 |
2 |
- |
- |
1000 |
20 |
- |
8 |
- |
25 |
- |
40 |
e'1 =566cos( ωt + 270º) e'3 =705sin( ωt - 180º)
|
||
3 |
3 |
100,5 |
- |
- |
88,5 |
- |
132,5 |
- |
25 |
- |
60 |
e'1 =70,5sin( ωt -13º) e'2 =68,5sin( ωt - 84º) e''2=56cos( ωt +100º) |
||
4 |
4 |
20,8 |
- |
52,7 |
15,1 |
- |
64,6 |
- |
65 |
- |
130 |
e'1 =100sin( ωt - 35º) e''1 =100sin( ωt +55º) e''3 =282sin( ωt - 40º) |
||
5 |
5 |
- |
250 |
- |
31.8 |
- |
66 |
- |
- |
100 |
50 |
e'1 =141cos( ωt + 270º) e'3 =141sin( ωt +90º)
|
||
6 |
6 |
- |
- |
159 |
15,9 |
- |
- |
- |
100 |
- |
10 |
e''1 =169sin ωt e'2 =169cos ωt e'3 =169 sin (ωt+ 180º)
|
||
7 |
7 |
24 |
- |
- |
12,7 |
5,5 |
- |
- |
- |
10 |
500 |
e''1 =282sin ωt e'2 =282sin( ωt - 180º)
|
||
8 |
8 |
13,6 |
- |
109,2 |
32,5 |
- |
94,6 |
- |
65 |
- |
70 |
e'1 =141cos( ωt - 90º) e''3 =282 sin( ωt-50º)
|
||
9 |
9 |
120 |
- |
- |
16 |
- |
8 |
- |
100 |
- |
200 |
e'1 =169sin( ωt +180º) e''2 =169cos ωt e'3 =169 cos( ωt+ 270º) |
||
10 |
10 |
12,7 |
47,8 |
- |
- |
31,9 |
- |
- |
25 |
- |
100 |
e'1 =70,5sin (ωt +20º) e'3 =84,6 sin (ωt -10º)
|
||
11 |
11 |
100 |
25 |
- |
- |
8 |
- |
- |
- |
100 |
159 |
e''1 =169sin (ωt +180º) e''2 =169sin ωt e'3 =169 cos ωt |
||
12 |
12 |
- |
80 |
145 |
- |
- |
44,5 |
60 |
- |
- |
120 |
e'2=689sin (ωt +12º) e''2 =496cos (ωt -150º) e'3 =705 sin( ωt+307º)
|
||
13 |
13 |
- |
- |
132 |
50 |
- |
184 |
- |
65 |
- |
50 |
e'1 =141cos( ωt + 345º) e'3 =200 sin( ωt+45º) e''3 =116 sin (ωt -11º)
|
||
14 |
14 |
- |
83,8 |
- |
- |
15,8 |
29,5 |
17 |
- |
- |
150 |
e'1 =113sin (ωt +338º) e'3 = 56,4 cos(ωt - 147º)
|
||
15 |
15 |
- |
63,8 |
- |
106 |
- |
- |
- |
- |
10 |
50 |
e'1 =99 sin (ωt+20º) e'2 =178cos ( ωt+270º)
|
||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
16 |
16 |
- |
477 |
125 |
- |
4 |
33 |
100 |
- |
- |
100 |
e''1 =141sin (ωt -270º) e''3 =141 cos( ωt - 90º)
|
17 |
17 |
- |
136 |
- |
- |
18,2 |
9,1 |
100 |
- |
- |
175 |
e''1 =169sin (ωt +90º) e'2 =169sin (ωt +180º) e''3 =169 cos( ωt - 90º) |
18 |
18 |
80 |
90 |
- |
10 |
5 |
- |
- |
- |
70 |
160 |
e'1 =141cos( ωt - 30º) e'2 =62 sin( ωt+326º) e''2 =96,5 cos(ωt +111º) |
19 |
19 |
- |
21,2 |
24,8 |
- |
- |
35,5 |
17 |
- |
- |
90 |
e'1 =80 sin (ωt+40º) e''1 =80 sin (ωt -50º) e'3 =56,4cos ( ωt - 180º)
|
20 |
20 |
21,2 |
- |
- |
- |
132,5 |
- |
- |
- |
25 |
60 |
e'1 =70,5sin ωt e'3 = 84,6 sin (ωt - 30º) |
21 |
1 |
- |
17,35 |
- |
- |
- |
40,15 |
17 |
- |
- |
110 |
e'1 =113sin ωt e'3 =46,2sin ωt e'3 = 32,4 sin (ωt - 90º) |
22 |
2 |
- |
49,75 |
500 |
10 |
79,6 |
4 |
- |
25 |
- |
80 |
e'1 =566cos( ωt-90º) e'3 =705 sin( ωt+180º)
|
23 |
3 |
402 |
- |
- |
354 |
- |
530 |
- |
25 |
- |
15 |
e'1 =70,5cos( ωt + 257º) e'2 =62 cos(ωt-174º) e''2 =56 sin (ωt - 170º) |
24 |
4 |
10,4 |
- |
26,35 |
7,55 |
- |
32,3 |
- |
65 |
- |
260 |
e''1 =141sin (ωt +10º) e'3 =200sin (ωt +5º) e''3 =200 sin (ωt -85º)
|
25 |
5 |
1600 |
250 |
- |
5,3 |
66 |
- |
- |
- |
100 |
50
|
e''1 =141sin ωt e'3 =141 cos ωt |
26 |
6 |
- |
- |
318 |
15,9 |
- |
15,9 |
- |
100 |
- |
100 |
e''1 =169sin ωt e'2 =169sin (ωt +90º) e'3 =169 sin (ωt -180º) |
27 |
7 |
16 |
- |
- |
- |
5,5 |
- |
- |
- |
10 |
500 |
e''1 =282sin ωt e'2 =282sin (ωt +180º)
|
28 |
8 |
13,6 |
- |
54,6 |
32,5 |
- |
- |
- |
65 |
- |
70 |
e''1 =141sin ωt e'3 =282 sin (ωt -50º)
|
29 |
9 |
60 |
- |
- |
8 |
- |
4 |
- |
100 |
- |
400 |
e'1 =169sin (ωt +180º) e''2 =169 sin (ωt +90º) e'3 =169 sin ωt
|
30 |
10 |
12,7 |
8 |
- |
- |
63,8 |
- |
- |
- |
25 |
100 |
e'1 =70,5sin (ωt +20º) e'3 =84,6sin (ωt -10º)
|
31 |
11 |
159 |
39,8 |
- |
- |
12,7 |
- |
- |
- |
100 |
100 |
e''1 =169sin (ωt -180º) e'2 =240sin (ωt +45º) e''2 =169 sin (ωt -90º) e'3 =169 cos ωt
|
32 |
12 |
- |
320 |
580 |
- |
- |
178 |
60 |
- |
- |
30 |
e'2 =689 cos(ωt -78º) e''2 =496 sin (ωt - 60º) e'3 =705sin (ωt -53º) |
33 |
13 |
- |
- |
26,3 |
12,5 |
- |
88,4 |
- |
65 |
- |
200 |
e'1 =200cos ωt e''1 =74,2sin (ωt +120º) e'3 =282 cos ( ωt+295º)
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
34 |
14 |
- |
41,9 |
19,13 |
- |
7,9 |
7,4 |
17 |
- |
- |
300 |
e'1 =113sin (ωt -22º) e'3 =56,4cos ( ωt-147º)
|
35 |
15 |
- |
127,6 |
- |
106 |
159 |
- |
- |
- |
10 |
50 |
e'1 =99sin (ωt-340º) e''2 =179 cos(ωt -90º)
|
36 |
16 |
- |
1600 |
250 |
- |
5,3 |
66 |
100 |
- |
- |
50 |
e'1 =282sin (ωt-135º) e''1 =400cos ( ω t-30º) e''3 =141 sin ωt |
37 |
17 |
- |
68 |
- |
- |
9,1 |
4,55 |
100 |
- |
- |
350 |
e'1 =169 cos(ωt -90º) e''1 =240sin (ωt +135º) e'2 =169sin (ωt +180º) e''3 =169 cos(ωt -90º)
|
38 |
18 |
320 |
360 |
- |
40 |
20 |
- |
- |
- |
70 |
40 |
e'1 =141sin (ωt -300º) e'2 =62 cos(ωt -124º) e''2 =96,4 sin (ωt +201º)
|
39 |
19 |
- |
10,6 |
24,8 |
- |
- |
13,8 |
17 |
- |
- |
180 |
e''1 =112,8 sin (ωt -5º) e'3 =56,4sin (ωt -40º)
|
40 |
20 |
12,7 |
31,8 |
- |
- |
39,8 |
- |
- |
- |
25 |
100 |
e'1 =70,5 cos(ωt+270º) e'3 =84,6cos ( ωt+240º)
|
41 |
1 |
- |
34,7 |
- |
- |
- |
80,3 |
17 |
- |
- |
55 |
e'1 =113,1sin ωt e'3 =56,6sin (ωt -35º)
|
42 |
2 |
- |
- |
500 |
10 |
- |
4 |
- |
25 |
- |
80 |
e'1 =620sin (ωt+54º) e''1 =538cos(ωt -158º) e'3 =705 cos ( ωt+90º) |
43 |
3 |
402 |
- |
228 |
354 |
- |
265 |
- |
25 |
- |
15 |
e'1 =70,5 cos(ωt -103º) e'2 =84,6sin (ωt +317º)
|
44 |
4 |
20,8 |
- |
52,7 |
15,1 |
- |
64,6 |
- |
65 |
- |
130 |
e''1 =141sin (ωt+10º) e''3 =282 sin (ωt -40º)
|
45 |
5 |
1060 |
413 |
- |
17,6 |
110 |
- |
- |
- |
100 |
30 |
e'1 =141 cos (ωt -90º) e'3 =141sin (ωt -270º)
|
46 |
6 |
- |
- |
318 |
31,8 |
- |
- |
- |
100 |
- |
50 |
e'1 =169sin ωt e'2 = 120sin (ωt +135º) e''2=120 cos(ωt -45º) e'3 =169sin (ωt -180º) |
47 |
7 |
48 |
- |
- |
25,4 |
11 |
- |
- |
- |
10 |
250 |
e''1 =282sin ωt e'2 =282 cos(ωt +90º)
|
48 |
8 |
6,8 |
- |
54,6 |
16,25 |
- |
47,3 |
- |
65 |
- |
140 |
e'1 =141 cos(ωt +270º) e'3 =282 cos(ωt -140º)
|
49 |
9 |
60 |
- |
- |
8 |
- |
14 |
- |
100 |
- |
150 |
e'1 =169sin (ωt +180º) e''2 =169 sin (ωt +90º) e'3 =169 sin ωt
|
50 |
10 |
12,7 |
8 |
- |
- |
128 |
- |
- |
- |
12 |
75 |
e'1 =70,5sin (ωt +20º) e'3 =84,6sin (ωt -10º)
|
