Тривимірні графіки. Побудова графіків поверхні
Для
побудови графіка двох змінних
необхідно виконати наступні дії:
сформувати в області побудови графіка прямокутну сітку, при цьому використовується функція meshgrid;
обчислити значення
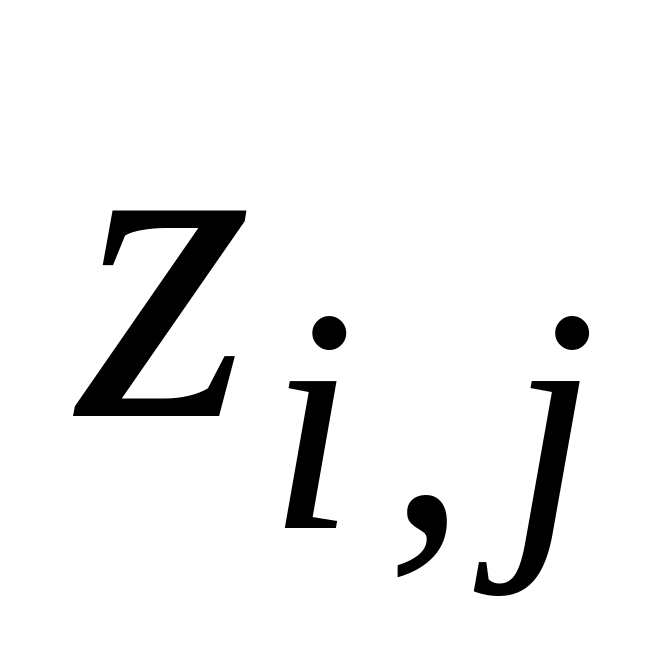по всіх вузлах сітки;звернутися до функції побудови поверхні mesh.
Команди:
- MESHGRID
Синтаксис:
[X, Y] = meshgrid(x, y)
Опис
Функція [X, Y] = meshgrid(x, y) формує масиви X і Y, що визначають координати вузлів прямокутника, що задається векторами x і y. Цей прямокутник задає область визначення функції від двох змінних, яку можна побудувати у виді 3D-поверхні.
- MESH
Синтаксис:
mesh(X, Y, Z) meshc(X, Y, Z) meshz(X, Y, Z)
mesh(X, Y, Z, C ) meshc(X, Y, Z, C ) meshz(X, Y, Z, C )
Опис:
Команда mesh виводить на екран сітчасту поверхню для значень масиву Z, визначених на множині значень масивів X і Y. Кольори вузлів поверхні задаються масивом C.
Команда meshc додатково до тривимірних поверхонь будує проекцію ліній постійного рівня.
Команда meshz додатково до тривимірних поверхонь будує площину відліку на нульовому рівні, закриваючи поверхню, що лежить нижче цього рівня.
- PLOT3
Синтаксис:
plot3(x, y, z)
Опис:
Команда plot3(...) є тривимірним аналогом функції plot(...).
Приклад.
Побудувати графік
функції
в області -
,
.
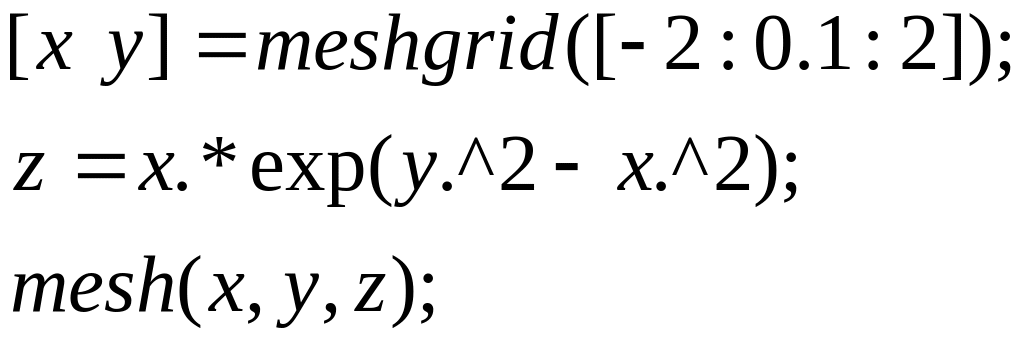
Приклад.
Побудувати
графік функції
,
де
,
.
Параметричне представлення функції
наступне:
.
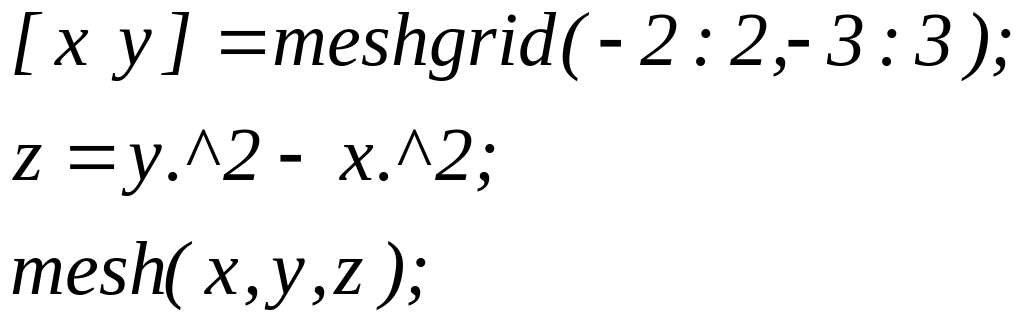
Приклад.
Побудувати
графік функції
.
Розв’язок
Розв’яжемо, застосувавши функцію surf.
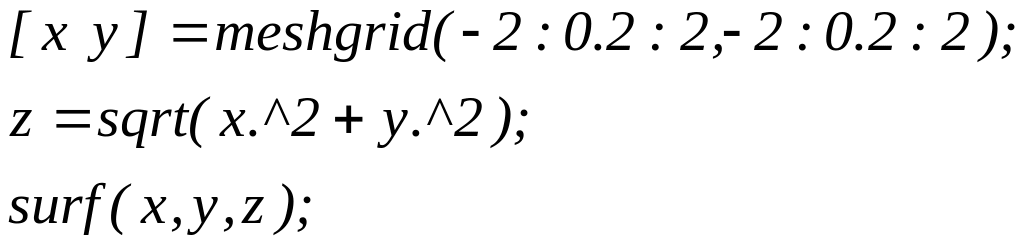
Анімація
При вивченні руху точки на площині та у просторі MatLab дозволяє побудувати графік руху і прослідкувати за ним. Для побудови анімаційного ролика існує дві функції: comet(x,y), comet3(x,y).
Приклад.
Показати рух точки на площині вздовж еліпса, що задається рівнянням
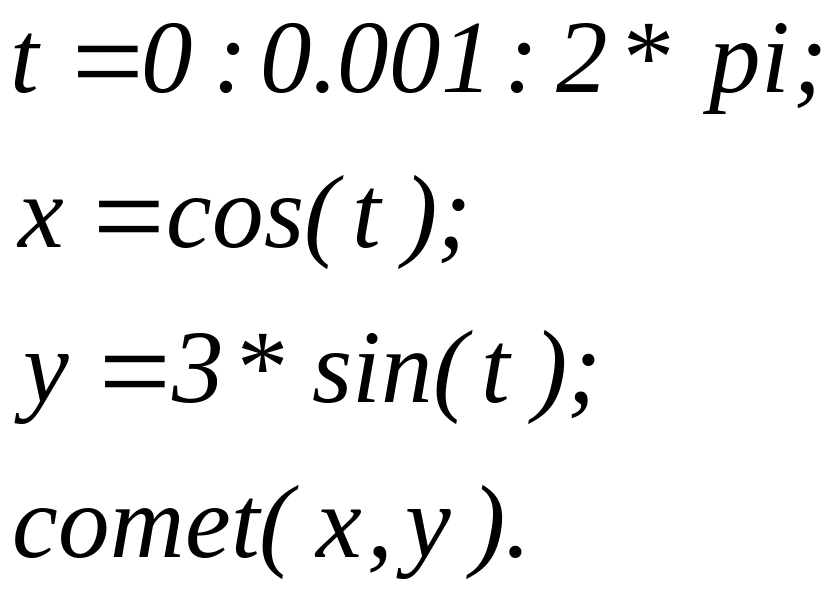
Приклад.
Показати рух точки у просторі вздовж гвинтової лінії, параметричне рівняння якої має вид
Побудова ліній рівня для тривимірної поверхні
CONTOUR
Синтаксис:
contour(x, y, Z)
Опис:
Команда contour(Z) рисує двовимірні лінії рівня для масиву даних Z, що визначає поверхню в тривимірному просторі без урахування діапазону зміни координат x і y.
Команда contour(x, y, Z), де x і y - вектори, рисує лінії рівня для масиву даних Z з урахуванням діапазону зміни координат x і y.
Обмеження:
При роботі з функцією contour передбачається, що елементи масивів x і y монотонно зростають.
Приклад:
Побудувати лінії рівня функції в області - , .
x = -2 : .2 : 2; y = x; [X, Y] = meshgrid(x); Z = X.* exp(- X.^2 - Y.^2); contour(X, Y, Z)
Побудова затіненої сітчастої поверхні
SURF
Синтаксис:
surf(X, Y, Z)
surf(Z)
Опис:
Команда surf(X, Y, Z, C) виводить на екран сітчасту поверхню для значень масиву Z, визначених на множині значень масивів X і Y. Колір осередку визначається масивом C.
Команда surf(Z, C) використовує сітку, що визначається одномірними масивами x = 1 : n і y = 1 : m.
Команди surf(X, Y, Z), surf(x, y, Z), surf(Z) використовують як масив кольору C = Z, тобто колір у цьому випадку пропорційний висоті поверхні.
Група команд surfc(...) на додаток до тривимірних затінених поверхонь будує проекцію ліній постійного рівня.
Приклад.
Побудуємо тривимірну затінену поверхню функції z = x * exp(-x2 - y2) зі шкалою затемненості.
[ X, Y ] = meshgrid([ -2 : 0.1 : 2 ]); Z = X . * exp(- X .^ 2 - Y .^ 2); surf(X, Y, Z) colormap(gray) shading interp colorbar
Приклад.
Побудувати сферу, що розфарбована відповідно до матриці Адамара (Hadamard), часто використовуваної в теорії кодування сигналів і складеної тільки з двох чисел 1 і -1.
k = 5; n = 2 ^ k - 1; [X, Y, Z]=sphere(n); C = hadamard(2 ^ k); surf(X, Y, Z, C); colormap([1 1 1; 2/3 2/3 2/3]) colorbar
Алгоритм:
У загальному виді, для завдання поверхні можна використовувати два незалежних параметри й і j, що змінюються безупинно, наприклад у прямокутнику 1 <= і <= m, 1 <= j <= n; тоді поверхня буде визначатися трьома функціями x(і, j), y(і, j), z(і, j). Коли й і j цілі числа, вони задають прямокутну сітку з цілочисельними значеннями для вузлів.